程序的表示、转换与链接：三、运算电路基础

一、整数加减运算理论

整数加减运算
- 无符号整数加减运算：指针、地址等通常被说明为无符号整数，因而在进行指针或地址运算时，需要进行无符号整数的加减运算
- 整数加减运算：无符号整数和带符号整数的加减运算电路一样，这个运算电路称为整数加减运算部件，基于带标志加法器实现。又由计算机中的加法器只有n位，因此是一种模 $2^n$ 运算系统

整数加减法溢出判断程序/思路

无符号数相加

溢出条件：红框内情况为溢出
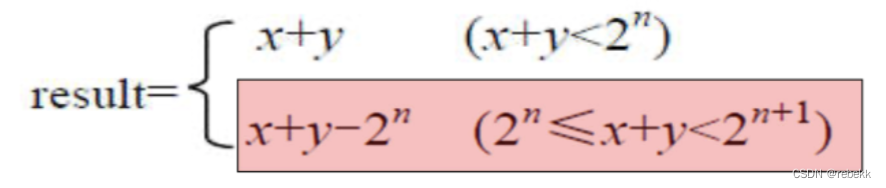
判断程序

int uadd_ok(unsigned x, unsigned y){unsigned sum = x + y;return sum >= x;
}

带符号数相加

溢出条件：
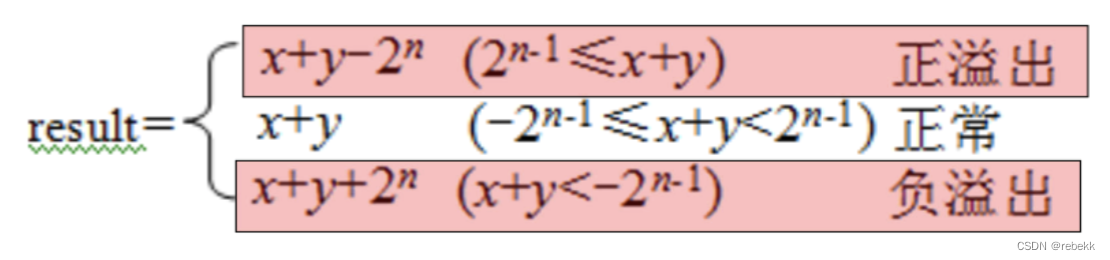
判断程序

int tadd_ok(int x, int y){int sum = x + y;int neg_over = x<0 && y<0 && sum>=0;int pos_over = x>=0 && y>=0 && sum<0;return !neg_over && !pos_over;
}

带符号数相减

判断程序

int tsub_ok(int x, int y){return tadd_ok(x, -y);
}

二、数字逻辑电路基础和整数加减运算部件

布尔代数：用0和1代表假和真，通过逻辑关系构建基于0和1的布尔代数运算，最基本的逻辑运算有与、或、非（如下图所示），任何一种逻辑表达式都可写成这三种基本运算的逻辑组合，如异或（XOR）
一位/n位逻辑门电路
- 逻辑门电路：可通过逻辑门电路来实现逻辑运算
  - 三种基本门电路：与门、或门、非门
  - 其他门电路可由三种基本门电路组合形成（如异或门电路）
- n位逻辑门电路：对于n位逻辑运算，只需重复使用n个相同的门电路即可
  - 如假设 $A=A_{n-1}A_{n-2}...A_1A_0, B=B_{n-1}B_{n-2}...B_1B_0$ ，则与运算 $F = A \cdot B$ 实际上是按位相与，即 $F_i=A_i·B_i (0\le i\le n-1)$
  - 假设逻辑值位数为n，则按位与、按位或、按位取反、按位异或的逻辑符号如下图所示：
组合逻辑部件
- 逻辑电路的两种类型：
  - 组合逻辑电路：没有存储功能，其输出仅依赖于当前输入
  - 时序逻辑电路：有存储功能，其输出不仅依赖于当前输入，还依赖于存储单元的当前状态
- 功能部件：即具有特定功能的组合逻辑部件，如译码器、编码器、多路选择器、加法器等，可利用基本逻辑门电路构成
- 实现一个功能部件的过程：1）用一个真值表描述功能部件的输入和输出之间的关系；2）根据真值表确定逻辑表达式；3）根据逻辑表达式实现逻辑电路
- 多路选择器MUX
  - 二路选择器：最简单的多路选择器。有两个输入端A、B，一个输出端F，一个控制端S。当S为0时，F=A；当S为1时，F=B
  - k路选择器：有k路输入，因而控制端S的位数应为 $\lceil log_2k\rceil$ 。如三路/四路选择器，S有两位；5～8路选择器，S有3位
ALU的核心电路：带标志加法器
- 一位加法器（全加器）
  - 规则：有两个加数A、B，低位进位为 $C_{in}$ ，本位和为F，向高位的进位为 $C_{out}$
  - 全加器真值表：
  - 逻辑表达式：
  - 全加器逻辑电路
  - 全加器符号：
- n位加法器（无符号整数加）
  - 规则：n位加法器可用n个全加器实现
  - 符号
  - 逻辑电路
  - 重要认识：
    - 加法是由逻辑部件实现的（如上面全加器的逻辑电路是由基本的与或非门实现的）
    - 其他所有算术运算（乘除法等）部件都基于加法器和（辅助的）逻辑运算实现
    - 因此，所有算术运算是基于0和1，以及逻辑运算实现的
- n位带标志加法器
  - 条件标志：零标志ZF、溢出标志OF、进/借位标志CF、符号标志SF称为条件标志。条件标志在运算电路中产生，被记录到专门的寄存器（程序/状态字寄存器或标志寄存器）中，如IA-32中的EFLAGS寄存器。条件标志的存在意义就是在分支指令（条件转移指令）中被用作是否执行转移的条件
  - 标志规则（OF和CF）
  - 符号：
  - 逻辑电路
- n位整数加/减运算器
  - 补码加减公式推导：
    
    其中：
  - 逻辑电路
    - 如上图，加减法运算统一采用加法来处理，实现减法的主要操作在于求 $B]_补$ （ $[A-B]_补=[A]_补+[-B]_补, [-B]_补=\bar B+1$ ）。当Sub为1时做减法，当Sub为0时做加法
    - 加法器不知道所运算的是带符号数还是无符号数
    - 加法器不判定对错，总是取低n位为结果，并生成标志信息
算术逻辑部件ALU
- 功能：进行基本算术运算和逻辑运算（无符号整数加减、带符号整数加减、与或非异或等逻辑运算）
- 核心电路：带标志加法器。输出和/差等结果，以及标志信息
- 有一个操作控制端ALUop：用来决定ALU所执行的处理功能。ALUop的位数k决定了操作的种类，如当k=3时，ALU最多有8种操作
- ALU符号：

三、如何启用逻辑电路：从C表达式到逻辑电路

由上可知，计算机中所有运算都是由相应的运算电路完成的，而这些运算电路是由基本的逻辑门电路实现的。

那么计算机是如何知道在运算电路中该执行什么操作？该对什么样的操作数进行运算的呢？

本节主要介绍高级语言程序中的表达式、运算类指令和运算电路之间的关系

C语言支持的基本数据类型
C语言支持的基本运算类型
- 算术：+、-、*、/、%、>、<、>=、<=、==、!=
- 按位：|、&、~、^
- 逻辑：||、&&、!
- 移位：<<、>>
- 扩展和截断
计算机如何实现高级语言程序（如C）中的运算（以y=(x>>2)+k为例）：
- 【C->指令】将各类表达式编译（转换）为指令序列：将y=(x>>2)+k转化为指令序列
  - sarw $2, %ax;（x>>2）
  - addw %bx, %ax;(x>>2+k)
- 【指令->电路】计算机直接执行指令来完成运算：控制器对指令进行译码，产生控制信号送运算电路
- 操作数在运算电路中运算（其中，移位器和整数加减器都是由逻辑门电路构成的）
  - sarw $2, %ax：将操作数“2”和“R[ax]”送移位器运算
  - addw %bx, %ax：将“R[ax]”和“R[bx]”送整数加减器中运算
将上述实现运算过程概括一下：
- 高级语言程序（如C）中的运算：整数/浮点数算术运算、按位/逻辑/移位/位扩展/位截断等运算
- 指令集中的运算：
  - 定点数运算：算术运算（带符号和无符号整数）和逻辑运算（与或非等逻辑操作）
  - 浮点数运算：浮点数的加减乘除
- 指令中的运算在运算电路中运行：ALU、通用寄存器组、其他部件

四、C语言中的各类运算

上面谈到高级语言程序中的各类运算，会被编译器转换为相应的运算指令，程序运行时，CPU执行这些指令，控制操作数在运算电路中被处理。

本节讲C语言程序中涉及的运算，如算术运算、按位运算、逻辑运算、移位运算等

算术运算：无符号整数、带符号整数、浮点数的加减乘除运算等
按位运算
- 用途：对位串实现“掩码”或其他操作（主要用于对多媒体数据或状态/控制信息进行处理）
- 操作：按位或“|”、按位与“&”、按位取反“～”、按位异或“^”

如若实现从数据y中提取低位字节，并使高位字节为0的话，可用“&”实现：作“y&0x00FF”。

移位运算
- 用途：提取部分信息、扩大或缩小2/4/8…倍
- 操作：左移“x<<k”、右移“x>>k”（若x为无符号数则进行逻辑左/右移；若x为带符号整数则进行算术左/右移）
逻辑运算
- 用途：用于关系表达式的运算。如if (x>y and i<100) then...中的and运算
- 操作：OR运算“||”、AND运算“&&”、NOT运算“!”
- 逻辑运算与按位运算的差别：符号表示不同（&& vs &）、运算过程不同（整体vs按位）、结果类型不同（逻辑值vs位串）