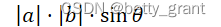玩玩二维凸包

前言&注明

最近在学计几（计算几何），然后……

精神状态越来越好了。（阿辉~）

本文只写了二维凸包的一种解法：扫描法。个人认为和 FHQ_Treap 一样，都是解同类问题的算法中易懂且好写。

网上的一些解析有点抽象（对于我），所以打算写一篇易懂（？）的讲解（给未来的自己）。

参考文献：

• 极角（From：百度百科）；
• 几何：极角排序详解；
• 数论小白都能看懂的平面凸包详解（From：洛谷，@ShineEternal）；
• 凸包（From：OI-Wiki）；
• 凸包算法详解（From：CSDN，@努力攻坚操作系统）。

参考文献有点多，这说明了什么？

正式启动之前，先去看看向量和角的弧度制表示法。

极角，启动！

BlastMike：你充710试试？

注意：极角一定要学，这东西没学就别想着学扫描法了。

极角

定义：在极坐标系中，平面上任何一点到极点的连线和极轴的夹角叫做极角。

光看定义十分的抽象，不如结合图来了解。

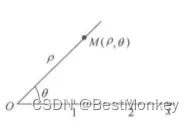
平面上取一定点 $O$，从 $O$ 引一条水平射线 $O_x$，规定方向自左至右，再选定一个长度单位并规定角旋转的正方向，通常取逆时针方向，这样就构成了一个极坐标系，如图所示，点 $O$ 叫作极点，射线 $O_x$ 叫作极轴。

在极坐标系中，平面上任意一点 $M$ 的位置，可以由 $OM$ 的长度 $\rho$ 和从到 $OM$ 的角 $\theta$ 来确定，把 $\rho$ 叫作点 $M$ 的极径，$\theta$ 叫作点M的极角，有序实数对 $(\rho ,\theta )$ 叫作点M的极坐标，记作$(\rho ,\theta )$。

特别地，当点 $M$ 在极点时，它的坐标是 $(0,\theta )$，$\theta$ 可以取任意值，当点M在极轴上时，它的坐标是 $(\rho ,0)$，$\rho$ 可以取任意正值。

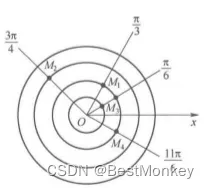
如图2所示，在极坐标系中，各点的极坐标分别为：$(2,\frac{\pi }{3}),(3,\frac{3\pi }{4}),(1,\frac{\pi }{6}),(2,\frac{11\pi }{6})$。

就学这么多就够了。

极角排序

这里讲利用叉积按极角从小到大排序。

设向量 ${}_a^{\to }$ ，${}_b^{\to }$，的叉积为 $x$。

对于 $x$：

• $x=0$：是指两向量平行（或者说两向量重合）；
• $x>0$：则 ${}_a^{\to }$ 在向量 ${}_b^{\to }$ 的顺时针方向（可理解为在 ${}_a^{\to }$ 在 ${}_b^{\to }$ 的下方）；
• $x<0$：则 ${}_a^{\to }$ 在 ${}_b^{\to }$ 的逆时针方向（可理解为在 ${}_a^{\to }$ 在 ${}_b^{\to }$ 的上方）。

学扫描法只需要这么多，其他可以自己拓展。

扫描法（Graham算法）开始

先说明这个算法的时间复杂度：$O(n\log n)$。

扫描法的第一步是对点集进行排序，这样能保证其有序性，从而在后续的处理中达到更高效的效果，所以扫描法比其他普通算法更优的原因。

例题：P2742 [USACO5.1] 圈奶牛Fencing the Cows /【模板】二维凸包 。

详细解释

(图片全 $\sum$ 洛谷的，懒得画)

假设共 $m$ 个点。

我们选择一个 $y$ 值最小的点，如有相同选 $x$ 最小的点，记为 $P_1$。

剩下的点集中按照极角的大小逆时针排序，然后编号为 $P_2\sim P_m$

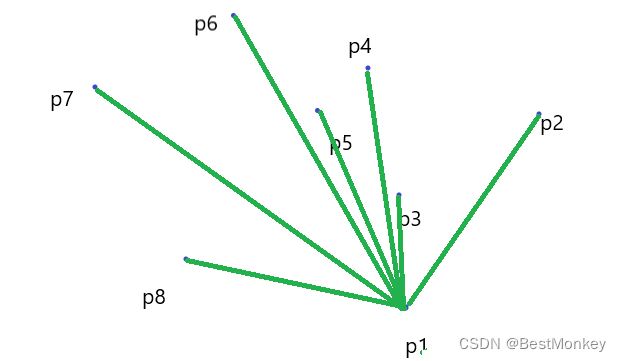
BlastMike：这是在种草？

我们按照排序结束后的顺序枚举每一个点，依次连线，可以使用一个栈来存储，每次入栈，如果即将入栈的元素与栈顶两个元素所构成了一个类似于凹壳（凹！）的东西，那么显然处于顶点的那个点一定不在这个点集的凸包上，而他正好在栈顶，所以把它弹出栈，新点入栈。

但是，新来的点有可能既踢走了栈顶，再连接新的栈顶元素后却发现仍然可以踢出，故此时就不能忘记判断。（不然会趋势）

如果你不想纠缠于繁杂的文字描述（简单地说就是语言认知能力差），那么下面就有动图解说献上。（早该说了）

至此，扫描法解释完成。

由于我们在排序的帮助下省去了一些盲目的扫描，虽然排序作为一个预处理时间复杂度占据了总时间复杂度，但相比 Andrew 算法还是更为优秀。

结合代码

检查叉积

计算叉积，检查叉积是否大于 $0$，如果是 $a$ 就逆时针转到 $b$。

代码片段：

inline double Cross(Point a, Point b, Point c) {return (b.x - a.x) * (c.y - a.y) - (c.x - a.x) * (b.y - a.y);
}

计算两点之间距离

这就不用解释了吧。

代码片段：

inline double Get_Distance(Point a, Point b) {return sqrt((a.x - b.x) * (a.x - b.x) * 1.0 + (a.y - b.y) * (a.y - b.y) * 1.0);
}

重要的排序函数

注意：这个函数别写错了，要不然功亏一篑。

判断叉积是否大于 $0$，若是，则一定满足要求（上面有说）。

特别的，若叉积等于 $0$，则说明两向量在同一直线上，要判断他们到 $p_0$（初始点）的距离。

代码片段：

inline bool Compar_2(Point a, Point b) {double m = Cross(Stack[0], a, b);if (m > 0)return 1;else if (m == 0 && Get_Distance(Stack[0], a) - Get_Distance(Stack[0], b) <= 0)return 1;else return 0;
}

Code

BlastMike：没有 Code 的 BestMonkey 的博客是没有灵魂的。

#include <bits/stdc++.h>
using namespace std;
struct Point {double x, y;
} P[100005], Stack[100005];
int n, Top = 1;
double Answer;
inline double Cross(Point a, Point b, Point c) {return (b.x - a.x) * (c.y - a.y) - (c.x - a.x) * (b.y - a.y);
}
inline double Get_Distance(Point a, Point b) {return sqrt((a.x - b.x) * (a.x - b.x) * 1.0 + (a.y - b.y) * (a.y - b.y) * 1.0);
}
inline bool Compar_1(Point a, Point b) {if (a.y == b.y)return a.x < b.x;return a.y < b.y;
}
inline bool Compar_2(Point a, Point b) {double m = Cross(Stack[0], a, b);if (m > 0)return 1;else if (m == 0 && Get_Distance(Stack[0], a) - Get_Distance(Stack[0], b) <= 0)return 1;else return 0;
}
signed main() {scanf("%d", &n);for (register int i = 0; i < n; ++i)scanf("%lf%lf", &P[i].x, &P[i].y);if (n == 1) puts("0.00"), exit(0);else if (n == 2) printf("%.2lf\n", Get_Distance(P[0], P[1])), exit(0);else {memset(Stack, 0, sizeof(Stack)), sort(P, P + n, Compar_1), Stack[0] = P[0], sort(P + 1, P + n, Compar_2), Stack[1] = P[1];//最低点一定在凸包里for (register int i = 2; i < n; ++i) {while (Cross(Stack[Top - 1], Stack[Top], P[i]) < 0)//判断前面点的会不会被踢走，如果被踢走那么出栈Top--;Stack[++Top] = P[i];}for (register int i = 0; i < Top; ++i)Answer += Get_Distance(Stack[i], Stack[i + 1]);Answer += Get_Distance(Stack[0], Stack[Top]), printf("%.2lf\n", Answer), exit(0);}return 0;
}

后记