search

bfs 和 dfs的相关的题目

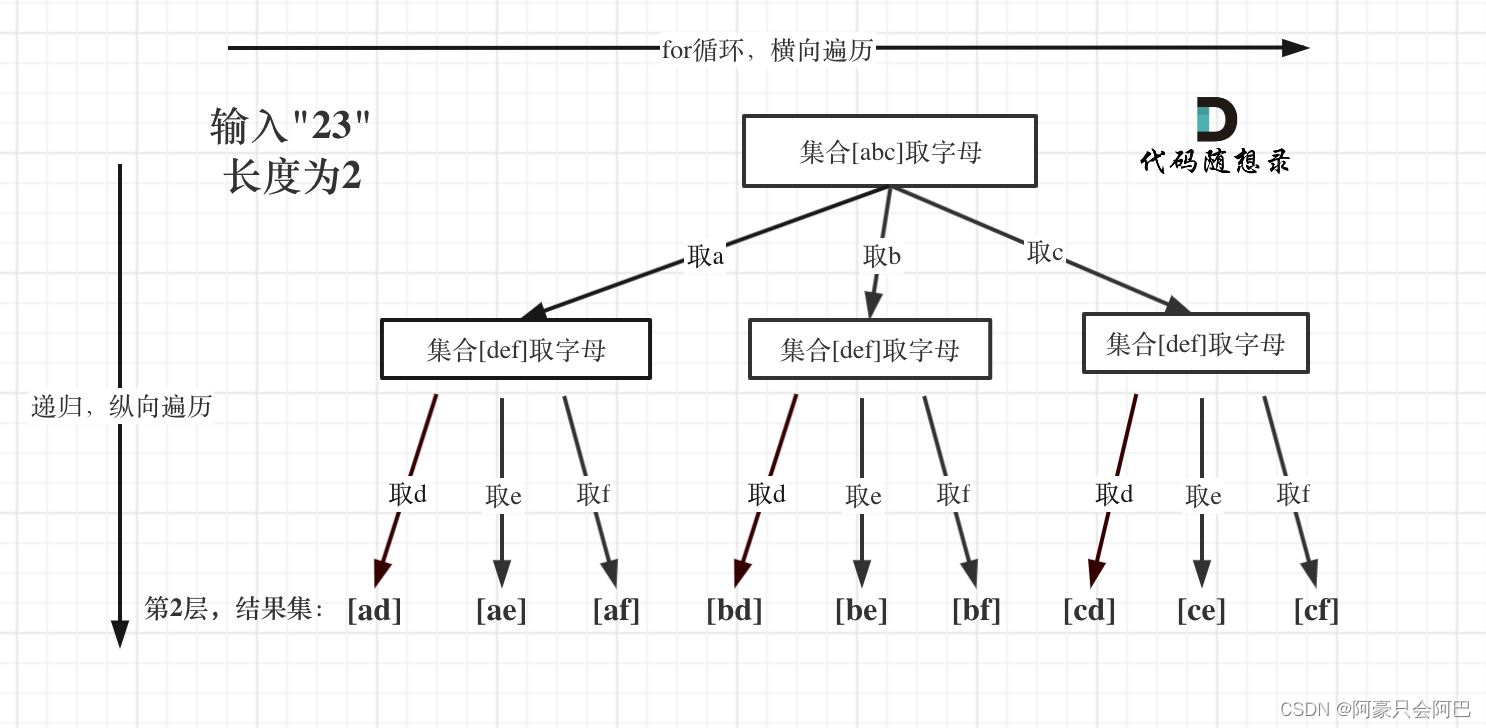
1. 全排列

题目: 给定一个数字列表，返回其所有可能的排列。

// premute(ans, nums, 0)
void permute(vector<vector<int> > &ans, vector<int> &nums, int k){if(k==nums.size()-1){ans.push_back(nums);}// 以k开头的所有排列for(int i=k;i<nums.size();i++){// 以每一个都作为开头，进行遍历swap(nums[i],nums[k]);permute(ans,nums,k+1);// 回溯swap(nums[i],nums[k]);}
}

2. 子集

题目: 给定一个可能具有重复数字的列表，返回其所有可能的子集。

// 调用函数dfs(res, sub, , nums, 0)之前, nums 必须首先排序, 
// sort(nums.begin(), nums.end());
void dfs(vector<vector<int>> &res, vector<int> &sub, vector<int> &nums, int k) {   res.push_back(sub);for(int i= k; i < nums.size(); i++) {// 跳过相同元素, if(i != k && nums[i] == nums[i - 1]) continue; sub.push_back(nums[i]);dfs(res, sub, nums, i + 1);// 回溯其他可能组合sub.pop_back();}
}

3. Word Break Problem

题目: 给一字串s和单词的字典dict,在字串中增加空格来构建一个句子，并且所有单词都来自字典。返回所有有可能的句子。
分析: 利用f[i]记录以i为起点的每个片段的终点j，并且片段要在字典中，然后从0位置开始搜索，每次给当前片段加上空格，然后以当前片段的末尾作为下一次搜索的头部，避免不必要的搜索。

vetor<int> f[1000];
vector<string> wordBreak(string &s, unordered_set<string> &wordDict) {n = s.length();int i, j;// 遍历所有可能的(i,j)组合,是否在字典中for (i = n - 1; i >= 0; --i) {for (j = i + 1; j <= n; ++j) {if (wordDict.find(s.substr(i, j - i)) != wordDict.end()) {// 大家请思考不加这个条件和加条件有什么区别,// if (j == n || f[j].size() > 0) //    f[i].push_back(j);f[i].push_back(j);}}}dfs(0, s, "");return res;
}
void dfs(int p, string s, string &now, vector<int> &res) {if(p == s.size()) {res.push_back(now);return;}if(p > 0) { // 找到一个单词划分now += " ";}   // 遍历所有以p开头, 以j结尾的划分进行dfsfor(int i = 0; i < f[p].size(); i ++) {dfs(f[p][i], s, now+s.substr(p, f[p][i]-p), res);}
}

4. K-Similar Strings

题目: 如果可以通过将 A 中的两个小写字母精确地交换位置 K 次得到与 B 相等的字符串，我们称字符串 A 和 B 的相似度为 K（K 为非负整数）。
给定两个字母异位词 A 和 B ，返回 A 和 B 的相似度 K 的最小值。
解析: 这是一个bfs的问题, 每次改变A的一个字符, 和B进行比较,
将改变后的A加入到候选队列中,直到所有出现A==B位置,得到此时的次数.

struct Node {string s;int step;Node(string _s, int _step):s(_s),step(_step);Node(){}
};int kSimilarity(string &A, string &B) {Node start(A, 0);queue<Node> q;set<string> vis;q.push(start);int ans = 0;while(q.size()) {Node str = q.front();q.pop();if(str.s == B) {ans = str.step;break;}int i = 0;while(str[i] == B[i]) i ++;for(int j = i + 1; j < B.size(); j ++) {if(str[j] != B[j] && str[j] == B[i]) {string temp = str;swap(temp[i], temp[j]);if(vis.find(temp) == vis.end()) {q.push(Node(temp, str.step+1));vis.insert(temp);}}}}return ans;
}

5. 无向图的联通块

题目: 给一个布尔类型的二维数组, 0 表示海, 1 表示岛。如果两个1是相邻的,那么我们认为他们是同一个岛.我们只考虑 上下左右 相邻. 求出岛屿的个数.
解析: 这就是无向图的联通块问题, 我们遍历所有是1的位置进行dfs(i,j), 并且将所有访问过的位置记录下来,如果当前位置是1,而且没有访问,则次数就加1.

void dfs(vector<vector<int>> &grid, int i, int j) {if(i < 0 || i >= grid.size()) return;if(j < 0 || j >= grid[0].size()) return;if(!grid[i][j]) return;grid[i][j] = 0;// 四个方向搜索dfs(grid, i-1, j);dfs(grid, i+1, j);dfs(grid, i, j-1);dfs(grid, i, j+1);
}
int numIslands(vector<vector<int>> &grid) {if (grid.empty() || grid[0].empty()) return 0;int N = grid.size(), M = grid[0].size();int cnt = 0;for (int i = 0; i < N; ++i) {for (int j = 0; j < M; ++j) {if (grid[i][j]) {dfs(grid, i, j);++cnt;}}}return cnt;
}

6. k个数的和

题目: 给定n个不同的正整数，整数k（1<= k <= n）以及一个目标数字。
在这n个数里面找出K个数，使得这K个数的和等于目标数字，你需要找出所有满足要求的方案。
解析: dfs(i, k, target)
每次怕判断是够使用第i个值, 如果使用, dfs(i+1,k-1,target-arr[i])
如果不使用, dfs(i+1,k,target),
if target == 0, 则表示满足要求,存储结果

void dfs(vector<int> A, int i, int k, int target, vector<int> &now, vector<vector<int>> &res) {if(i > A.size() || target < 0 || k < 0) return;if(target == 0 && k==0) {res.push_back(now);return;}// usernow.push_back(A[i]);dfs(A, i+1, k-1, target-A[i], now, res);now.pop_back();// not use idfs(A, i+1, k, target, now, res);}
vector<vector<int>> kSumII(vector<int> &A, int k, int target) {// write your code herevector<vector<int>> res;vector<int> now;dfs(A,0,k,target,now,res);return res;}

7. 单词接龙

题目: 给出两个单词（start和end）和一个字典，找出从start到end的最短转换序列，输出最短序列的长度。
变换规则如下：

• 每次只能改变一个字母。
• 变换过程中的中间单词必须在字典中出现。(起始单词和结束单词不需要出现在字典中)

解析: 使用bfs进行变换,每一修改一个字符[‘a’–‘z’],判断是否在字典中,并记录当前的步数.

int ladderLength(string &start, string &end, unordered_set<string> &dict) {int length = 2;    if(start == end) return 1;queue<string> q;q.push(start);while(!q.empty()){int size = q.size();// 对每一个层以此处理, 这一个的都步数一样for(int i=0;i<size;i++){string tmp = q.front();q.pop();// 遍历tmp的所有的字符，进行26个字符的变换for(int j=0;j<tmp.size();j++){// 要记录老字符，因为最后要恢复char oldc = tmp[j];for(char c='a';c<='z';c++){if(tmp[j] == c) continue;tmp[j] = c;//验证是否已经满足条件if(tmp == end) return length;// 变换的单词是否在字典中if(dict.find(tmp) != dict.end()){q.push(tmp);dict.erase(tmp); // 防止多次使用}}// 恢复当前的变化,这个不变，变化下一个,tmp[j] = oldc;}}length ++;}return length;
}

8. 单词搜索

题目:
给出一个二维的字母板和一个单词，寻找字母板网格中是否存在这个单词。单词可以由按顺序的相邻单元的字母组成，其中相邻单元指的是水平或者垂直方向相邻。每个单元中的字母最多只能使用一次。

样例
样例 1:输入：["ABCE","SFCS","ADEE"]，"ABCCED"
输出：true
解释：
[    A B C ES F C S A D E E
]
(0,0)A->(0,1)B->(0,2)C->(1,2)C->(2,2)E->(2,1)D
样例 2:输入：["z"]，"z"
输出：true
解释：
[ z ]
(0,0)z

bool dfs(int i, int j, int k, vector<vector<char>> &board, string word, vector<vector<int>> &vis) {if(board[i][j] == word[k]) {++ k;if(k == word.size()) {return true;}}else return false;bool flag = false; vis[i][j] = 1;if(i-1 >=0 && (!vis[i-1][j]) && board[i-1][j] == word[k]) flag = flag | dfs(i-1, j, k, board, word, vis); if(flag) return flag;if(i+1 < board.size() && (!vis[i+1][j]) && board[i+1][j] == word[k]) flag = flag | dfs(i+1, j, k, board, word, vis); if(flag) return flag;if(j-1 >= 0 && (!vis[i][j-1]) && board[i][j-1] == word[k]) flag = flag | dfs(i, j-1, k, board, word, vis);if(flag) return flag;if(j+1 <= board[0].size() && (!vis[i][j+1]) && board[i][j+1] == word[k]) flag = flag | dfs(i, j+1, k, board, word, vis);// 下次使用标记vis[i][j] = 0;return flag;
}    
bool exist(vector<vector<char>> &board, string &word) {if(board.empty() || board[0].size() == 0) return false;bool res = false;vector<vector<int>> vis(board.size(), vector<int>(board[0].size(), 0));for(int i = 0; i < board.size(); i ++) {for(int j = 0; j < board[i].size(); j ++) {if(word[0] == board[i][j] && dfs(i,j,0,board,word, vis)){return true;                    }}}return res;   
}

9. 分割字符串

题目: 给一个字符串,你可以选择在一个字符或两个相邻字符之后拆分字符串,使字符串由仅一个字符或两个字符组成,输出所有可能的结果.
解析： dfs(s) = dfs(s-1) + dfs(s-2)

void dfs(int i, string s, vector<string> &now, vector<vector<string>> &res) {if(i == s.size()) {res.push_back(now);return;}if(s.size() - i == 1) {now.push_back(s.substr(i, 1));dfs(i+1,s,now,res);now.pop_back();return;}if(s.size() - i >= 2) {now.push_back(s.substr(i, 1));dfs(i+1,s,now,res);    now.pop_back();now.push_back(s.substr(i, 2));dfs(i+2,s,now,res);now.pop_back();}    
} 
vector<vector<string>> splitString(string& s) {vector<string> now; vector<vector<string>> res;dfs(0,s,now,res);    return res;
}

10. 划分回文串

题目: 给定一个字符串S，将S切分成每一个子串都是回文串，返回所有可能的结果.

Input  : s = "bcc"
Output : [["b", "c", "c"], ["b", "cc"]]

bool checkPalindrome(string str) { int len = str.length(); len--; for (int i=0; i<len; i++) { if (str[i] != str[len]) return false; len--; } return true; 
} 
void addStrings(vector<vector<string> > &v, string &s, vector<string> &temp, int index) { int len = s.length(); string str; vector<string> current = temp; if (index == 0) temp.clear(); for (int i = index; i < len; ++i) { str = str + s[i]; if (checkPalindrome(str)) { temp.push_back(str); if (i+1 < len) addStrings(v,s,temp,i+1); elsev.push_back(temp); temp = current; } } return; 
}