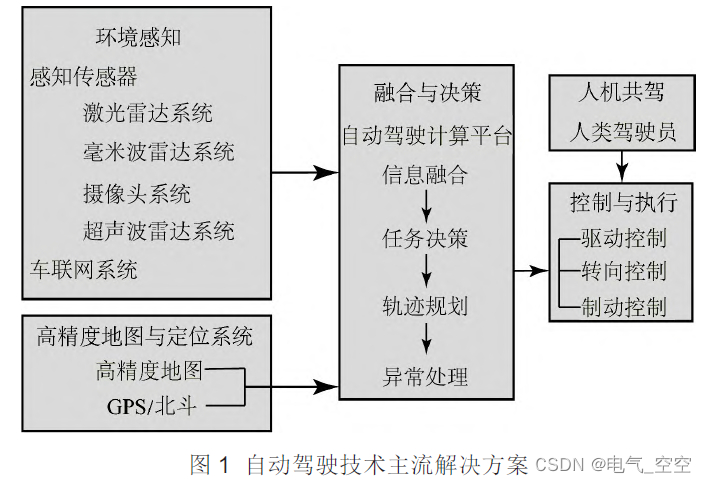
一 微积分
1.1 导数和微分
微分就是求导:
%matplotlib inline
import numpy as np
from matplotlib_inline import backend_inline
from d2l import torch as d2l
def f(x):return 3 * x ** 2 - 4 * x定义:
然后求 f(x) 在 x = 1 时的导数,实际导数: = 2*3*1(x=1) - 4 = 2
def numerical_lim(f, x, h):return (f(x + h) - f(x)) / hratio = 0.1
for i in range(5):print(f'ratio={ratio:.5f}, y_={numerical_lim(f, 1, ratio):.5f}')ratio *= 0.1# ratio=0.10000, y_=2.30000
# ratio=0.01000, y_=2.03000
# ratio=0.00100, y_=2.00300
# ratio=0.00010, y_=2.00030
# ratio=0.00001, y_=2.00003当 ratio 越小的时候,倒数越接近我们要求的值, 画出x=1此时的原函数和切线函数看下。
x = np.arange(-2, 4, 0.1)
plot(x, [f(x), 2 * x - 3], 'x', 'y', legend=['y=3x²-4x', 'y=2x−3'], figsize=(6, 6))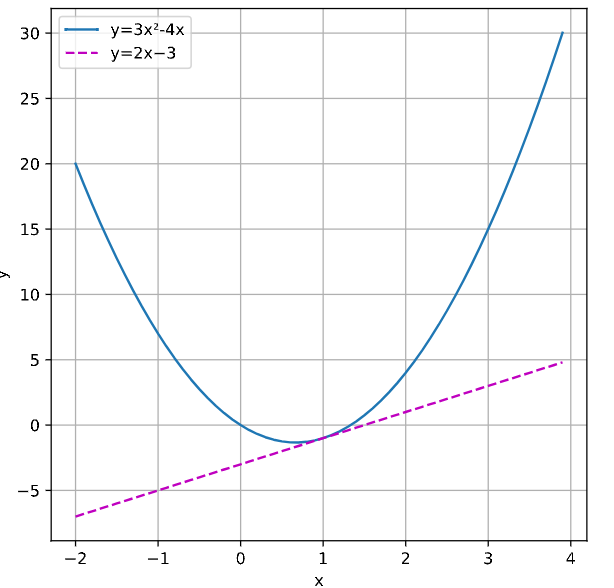
偏导数,梯度:
连结一个多元函数对其所有变量的偏导数,来得到该函数的梯度(gradient)向量。
对于这种固定的函数可以直接计算它的导数,也就是梯度,机器学习的线性回归模型就是用的该方式直接计算,机器学习模块写过该计算过程。
1.2 自动微分
求导是几乎所有深度学习优化算法的关键步骤。
假设我们想对函数 关于列向量x求导。首先,我们创建变量x并为其分配一个初始值。
对应的数学公式:
import torch
x = torch.arange(4.0)
x
# tensor([0., 1., 2., 3.])计算y关于x的梯度之前,需要一个地方来 存储梯度。
x.requires_grad_(True) # 等价于x=torch.arange(4.0,requires_grad=True)
print(x.grad)
# None # 默认值是None计算y,torch.dot() 点积的计算规则是将两个向量对应位置的元素相乘,然后将 结果相加 得到一个标量值。
print(x)
y = 2 * torch.dot(x, x) # 点积 # (1*1+2*2+3*3)*2=28
y
# tensor([0., 1., 2., 3.], requires_grad=True)
# tensor(28., grad_fn=<MulBackward0>)x是一个长度为4的向量,计算x和x的点积,得到了我们赋值给y的标量输出。接下来,通过调用反向传播函数 来自动计算y关于x每个分量的梯度,并打印这些梯度。
y.backward()
x.grad
# tensor([ 0., 4., 8., 12.])函数 关于x的梯度应为 y=4x。
x.grad == 4 * x
# tensor([True, True, True, True])1.3 继续计算另一个函数的自动微分
先梯度清零:
# 在默认情况下,PyTorch会累积梯度,我们需要清除之前的值
x.grad.zero_()
print(x.grad)
# tensor([0., 0., 0., 0.])将所有x求和求导, 函数:y=x,导数:
y = x.sum() # y=0+1+2+3
print(x,y)
y.backward()
x.grad
# tensor([0., 1., 2., 3.], requires_grad=True) tensor(6., grad_fn=<SumBackward0>)
# tensor([1., 1., 1., 1.])1.4 非标量变量的反向传播
当y不是标量时,向量y关于向量x的导数的最自然解释是一个矩阵。对于高阶和高维的y和x,求导的结果可以 是一个高阶张量。
先梯度清零:
x.grad.zero_()
print(x.grad) # tensor([0., 0., 0., 0.])函数: , 导函数:y = 2x。
y = x * x
print(x, y)
# 等价于y.backward(torch.ones(len(x)))
y.sum().backward()
x.grad
# tensor([0., 1., 2., 3.], requires_grad=True)
# tensor([0., 1., 4., 9.], grad_fn=<MulBackward0>)
# tensor([0., 2., 4., 6.])1.5 分离计算
梯度清零,先合并计算查看梯度::
# 在默认情况下,PyTorch会累积梯度,我们需要清除之前的值
x.grad.zero_()
print(x.grad)
# tensor([0., 0., 0., 0.])y = x * x * x
print(x, y)
# 等价于y.backward(torch.ones(len(x)))
y.sum().backward()
x.grad # tensor([ 0., 3., 12., 27.])
# tensor([0., 1., 2., 3.], requires_grad=True)
# tensor([ 0., 1., 8., 27.], grad_fn=<MulBackward0>)
# tensor([ 0., 3., 12., 27.])有时,我们希望 将某些计算移动到记录的计算图之外。例如,假设y是作为x的函数计算的,而z则是作为y和x的 函数计算的。想象一下,我们想计算z关于x的梯度,但由于某种原因,希望将y视为一个常数,并且 只考虑 到x在y被计算后发挥的作用。
分离计算,先梯度清零:
# 在默认情况下,PyTorch会累积梯度,我们需要清除之前的值
x.grad.zero_()
print(x.grad)
# tensor([0., 0., 0., 0.])print('x:', x)
y = x * x # 导函数: y=2x, 梯度:[0, 2, 4, 6]
print('y:', y)
u = y.detach()
print('u:', u)z = u * x # y = x^3 导函数:y = 3x^2 梯度:[0, 3, 12, 27]
print('z:', z)
z.sum().backward()
print('x.grad:', x.grad)
print('x.grad == u:', x.grad == u)
x.grad # x: tensor([0., 1., 2., 3.], requires_grad=True)
# y: tensor([0., 1., 4., 9.], grad_fn=<MulBackward0>)
# u: tensor([0., 1., 4., 9.])
# z: tensor([ 0., 1., 8., 27.], grad_fn=<MulBackward0>)
# x.grad: tensor([0., 1., 4., 9.])
# x.grad == u: tensor([True, True, True, True])
# tensor([0., 1., 4., 9.]) 分开计算后,x的梯度并不是按 函数 来计算的,而是使用的中间计算的变量
,即是梯度不会向后流经u到x。
由于记录了y的计算结果,我们可以随后在y上调用反向传播,得到 关于的x的导数,即2x。
x.grad.zero_()
y.sum().backward()
print('x.grad == 2 * x:', x.grad == 2 * x)
x.grad
# x.grad == 2 * x: tensor([True, True, True, True])
# tensor([0., 2., 4., 6.])分离计算后将 函数: 拆分为了两个函数:y = kx 和
。
1.6 Python控制流的梯度计算
使用自动微分的一个好处是:即使构建函数的计算图需要通过Python控制流,我们仍然可以计算得到的变量的梯度。
def f(a):b = a * 2while b.norm() < 1000:# print('b:', b)b = b * 2if b.sum() > 0:c = belse:c = 100 * breturn c给个初始值a,经过程序n次计算后得到结果值 d, 然后使用结果值和a计算梯度:
# a = torch.randn(size=(), requires_grad=True)
a = torch.tensor([10.], requires_grad=True)
d = f(a)
print(f'a:{a}, d:{d}')
d.backward()
a.grad# a:tensor([10.], requires_grad=True), d:tensor([1280.], grad_fn=<MulBackward0>)
# tensor([128.])1280 / 10 = 128 # 此时的梯度128。
a.grad == d / a
# tensor([True])二 概率
掷骰子,想知道看到1的几率有多大,一共六个面,随机抽样:
%matplotlib inline
import torch
from torch.distributions import multinomial
from d2l import torch as d2lfair_probs = torch.ones([6]) / 6
multinomial.Multinomial(1, fair_probs).sample()
# tensor([0., 0., 0., 0., 1., 0.])使用深度学习框架的函数同时抽取多个样本,得到我们想要的任意形状的独立样本数组。
multinomial.Multinomial(10, fair_probs).sample()
# tensor([1., 0., 1., 1., 6., 1.])# 将结果存储为32位浮点数以进行除法
counts = multinomial.Multinomial(1000, fair_probs).sample()
counts / 1000 # 相对频率作为估计值# tensor([0.1730, 0.1590, 0.1780, 0.1640, 0.1730, 0.1530])因为我们是从一个公平的骰子中生成的数据,我们知道每个结果都有真实的概率1 6,大约是0.167,所以上面 输出的估计值看起来不错。
我们也可以看到这些概率如何随着时间的推移收敛到真实概率。让我们进行 500组实验,每组抽取10个样本。
counts = multinomial.Multinomial(10, fair_probs).sample((500,))
cum_counts = counts.cumsum(dim=0)estimates = cum_counts / cum_counts.sum(dim=1, keepdims=True)
d2l.set_figsize((6, 4.5))
for i in range(6):d2l.plt.plot(estimates[:, i].numpy(), label=("P(die=" + str(i + 1) + ")"))
d2l.plt.axhline(y=0.167, color='black', linestyle='dashed')
d2l.plt.gca().set_xlabel('Groups of experiments')
d2l.plt.gca().set_ylabel('Estimated probability')
d2l.plt.legend()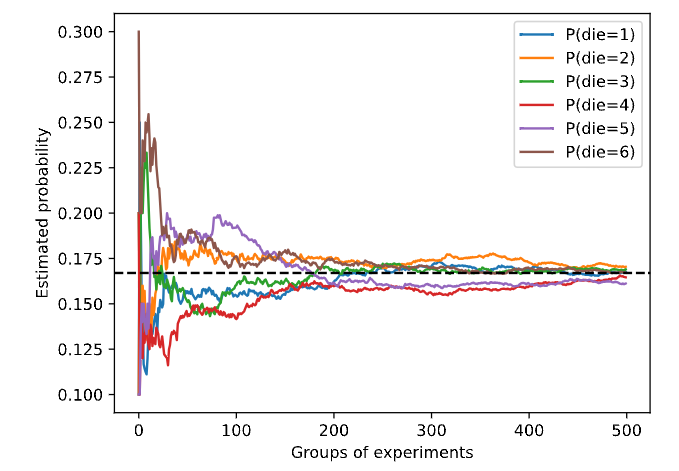
每条实线对应于骰子的6个值中的一个,并给出骰子在每组实验后出现值的估计概率。当我们 通过更多的实 验获得更多的数据时,这6条实体曲线向真实概率收敛。