推荐阅读
智能化校园:深入探讨云端管理系统设计与实现(一)
智能化校园:深入探讨云端管理系统设计与实现(二)
文章目录
- 推荐阅读
- 二分查找
- 题目
- 思路
- 解法
- 左闭右闭式写法
- 左闭右开式写法
二分查找
题目
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
提示:
- 你可以假设 nums 中的所有元素是不重复的。
- n 将在 [1, 10000]之间。
- nums 的每个元素都将在 [-9999, 9999]之间。

思路
二分查找最常用的场景:寻找一个数、寻找左侧边界、寻找右侧边界。
而看到该题目给出的提示,数组为有序数组,数组元素不重复。这些不就是使用二分法的前提条件嘛。
使用二分法时主要需要注意区间的定义,区间的定义就是不变量,要在二分查找的过程中,保持不变量,就是在while寻找中每一次边界的处理都要坚持根据区间的定义来操作,这就是循环不变量规则。
而在写二分法的时候,区间的定义一般为两种,左闭右闭即[left, right],或者左闭右开即[left, right)。
解法
左闭右闭式写法
左闭右闭,即区间定义为[left,right],那么while条件中,采用的是<=,即 left<=right,if中的判断条件则要根据情况赋值
- nums[middle] > target,right=middle-1;
- nums[middle] < target,left=middle+1;
代码示例:
class Solution {public int search(int[] nums, int target) {
// 避免当 target 小于nums[0] nums[nums.length - 1]时多次循环运算if (target < nums[0] || target > nums[nums.length - 1]) {return -1;}int left=0;int right=nums.length-1;while(left<=right){int middle=(left+right)/2;if(nums[middle]>target){right=middle-1;}else if(nums[middle]<target){left=middle+1;}else return middle;}return -1;}
}
- 时间复杂度:O(log n)
- 空间复杂度:O(1)
左闭右开式写法
左闭右开,即区间定义为[left,right),那么while条件中,采用的是<,即 left<right, if 中的判断条件则要根据情况赋值
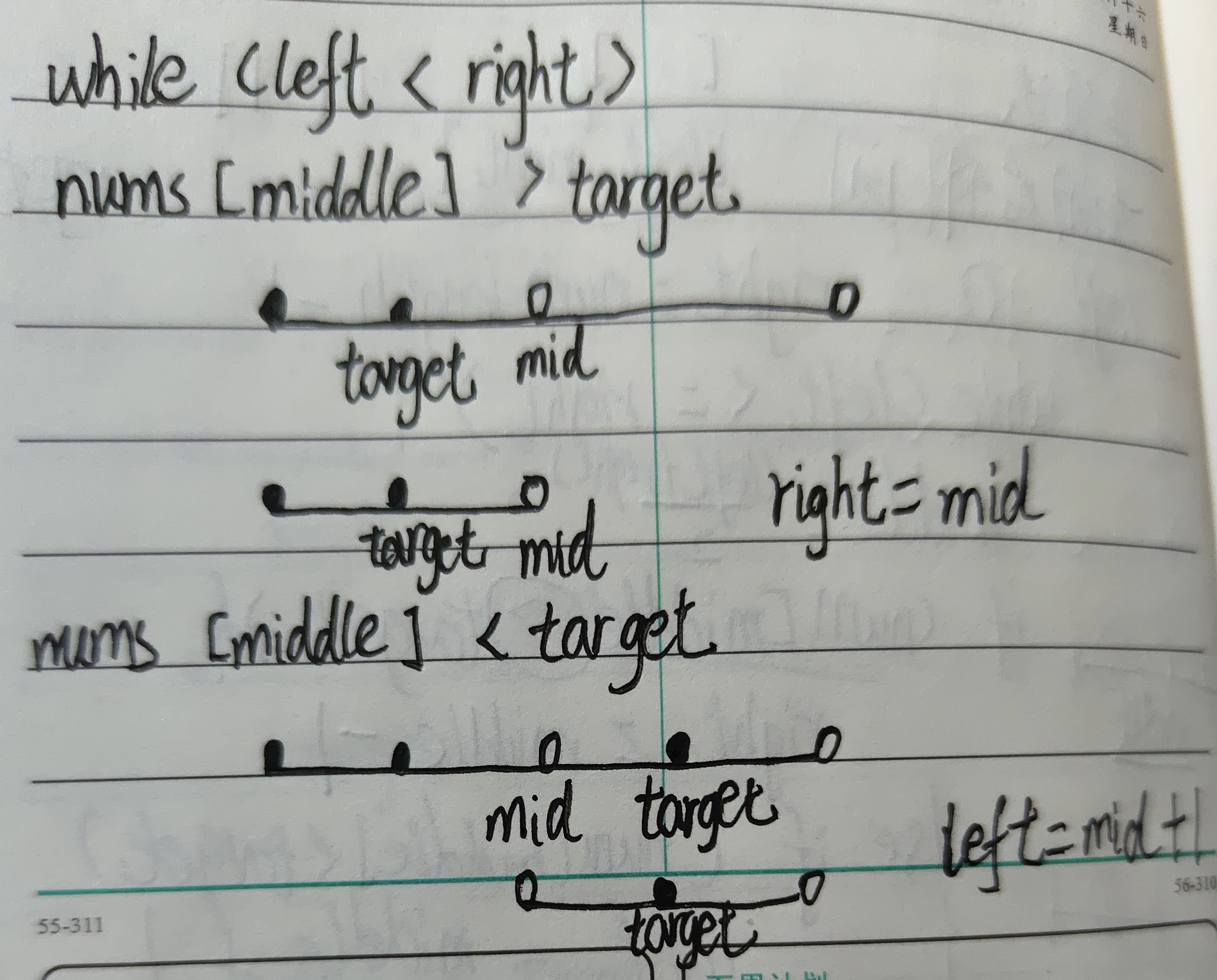
- nums[middle] > target,right=middle;
- nums[middle] < target,left=middle+1;
代码示例:
class Solution {public int search(int[] nums, int target) {
// 避免当 target 小于nums[0] nums[nums.length - 1]时多次循环运算if (target < nums[0] || target > nums[nums.length - 1]) {return -1;}int left = 0;int right = nums.length;while (left < right) {int middle = (left + right) / 2;if (nums[middle] > target) {right = middle;} else if (nums[middle] < target) {left = middle+1;} else return middle;}return -1;}
}
- 时间复杂度:O(log n)
- 空间复杂度:O(1)