KK线实战分析系列之六:启明星——空方力量减弱信号
- 一、星线
- 二、多种反转形态
- 三、启明星形态
- 四、启明星形态的总结
一、星线
星线在单根K线形态上是属于纺锤线,之所以被称为星线,主要是因为它在行情当中的相对位置,区别于其他纺锤线的一点是它的实体与前面的K线的实体之间形成了一个价格跳空区域。
一个小实体的K线就这样被抛出去了,到了空中,就像是一颗孤立的星星一样,详细一点说星线的实体,可以在前一根K线的影线范围之内,只是不与实体部分相重合,
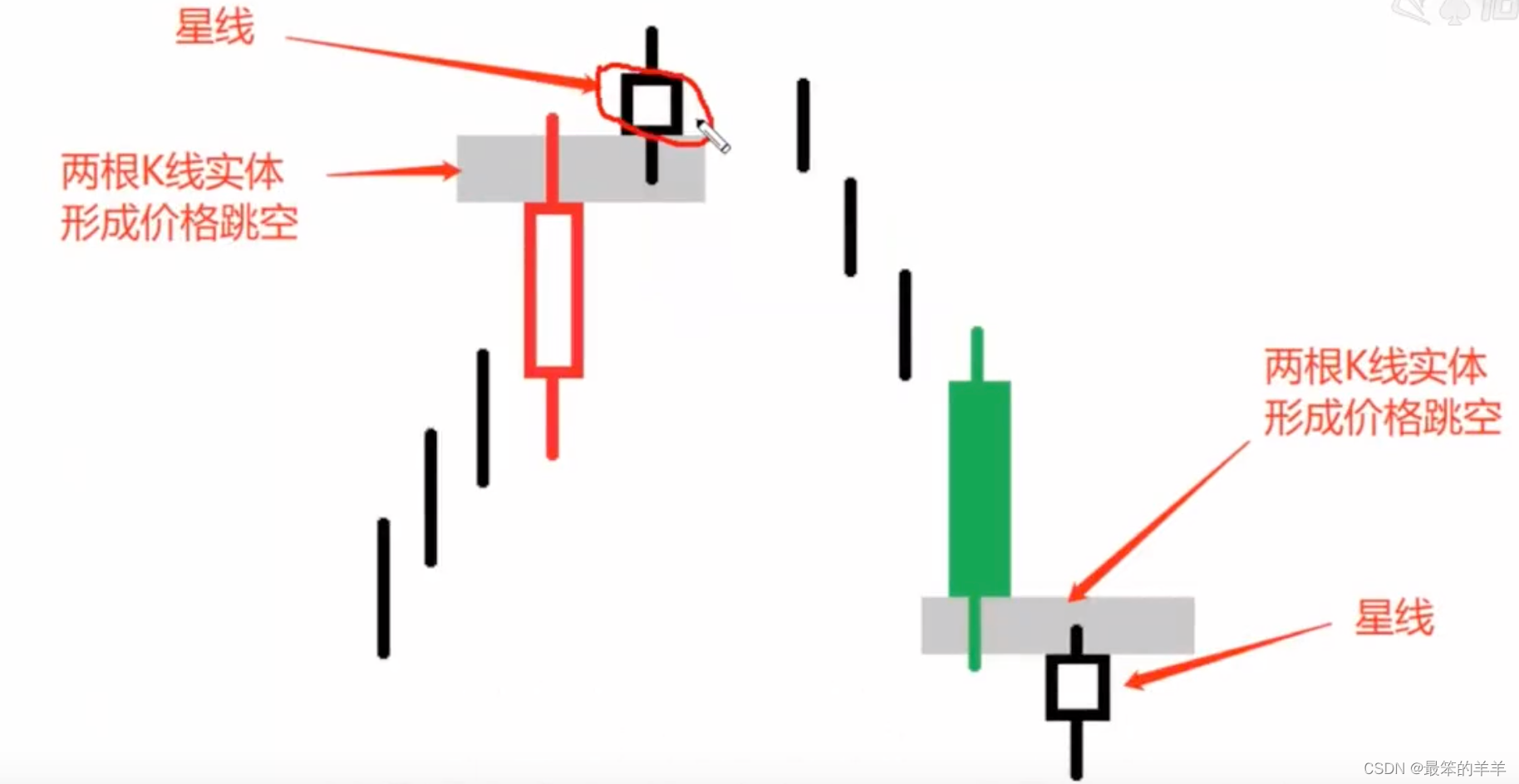

如果K线特别小,意味着这个时段的开盘价与收盘价非常接近,或者干脆相等,就是十字星。
总的来说,星线因为实体较小,在涨势或者跌势当中出现,意味着多空双方进入僵持的状态。
二、多种反转形态
- 启明星形态
- 黄昏星形态
- 十字星形态
- 流星形态
以上反转形态中,星线都是其中重要组成部分。
三、启明星形态
- 底部反转形态
- 启明星形态暗示着太阳将升起,天要亮了,有朝气,预示着行情上涨
- 这个形态由三根K线组成
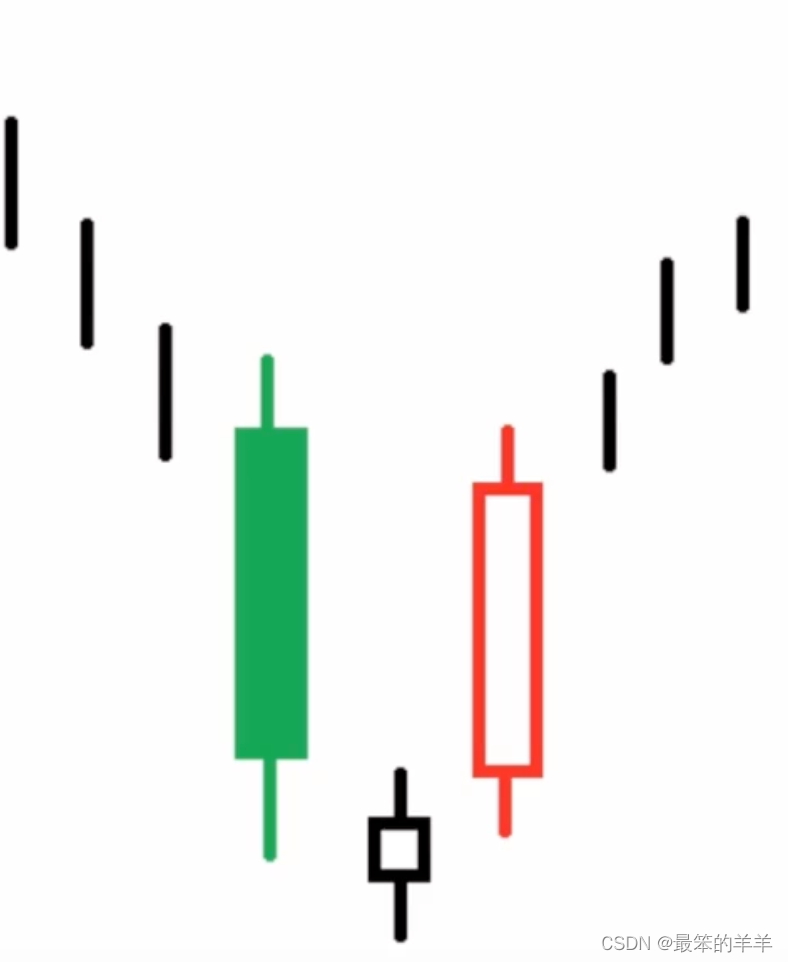
- 中间这个纺锤线可以说阴线也可以是阳线
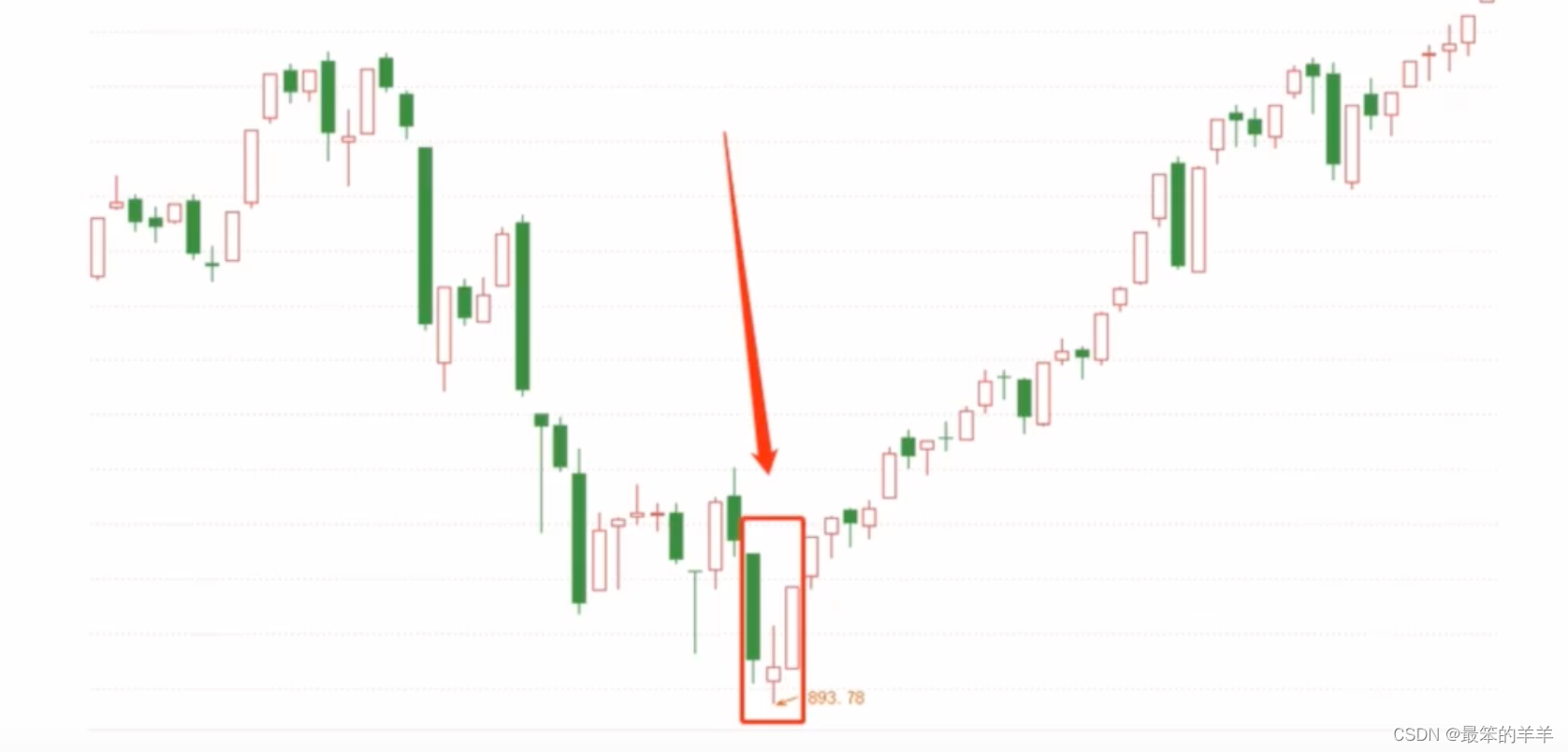
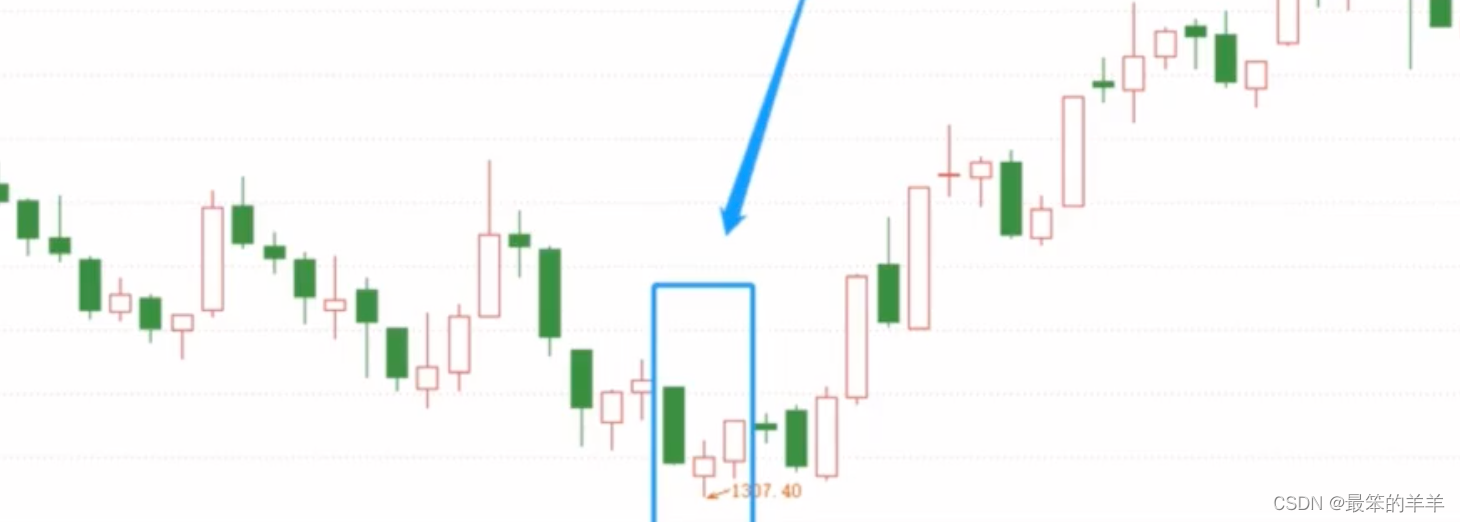
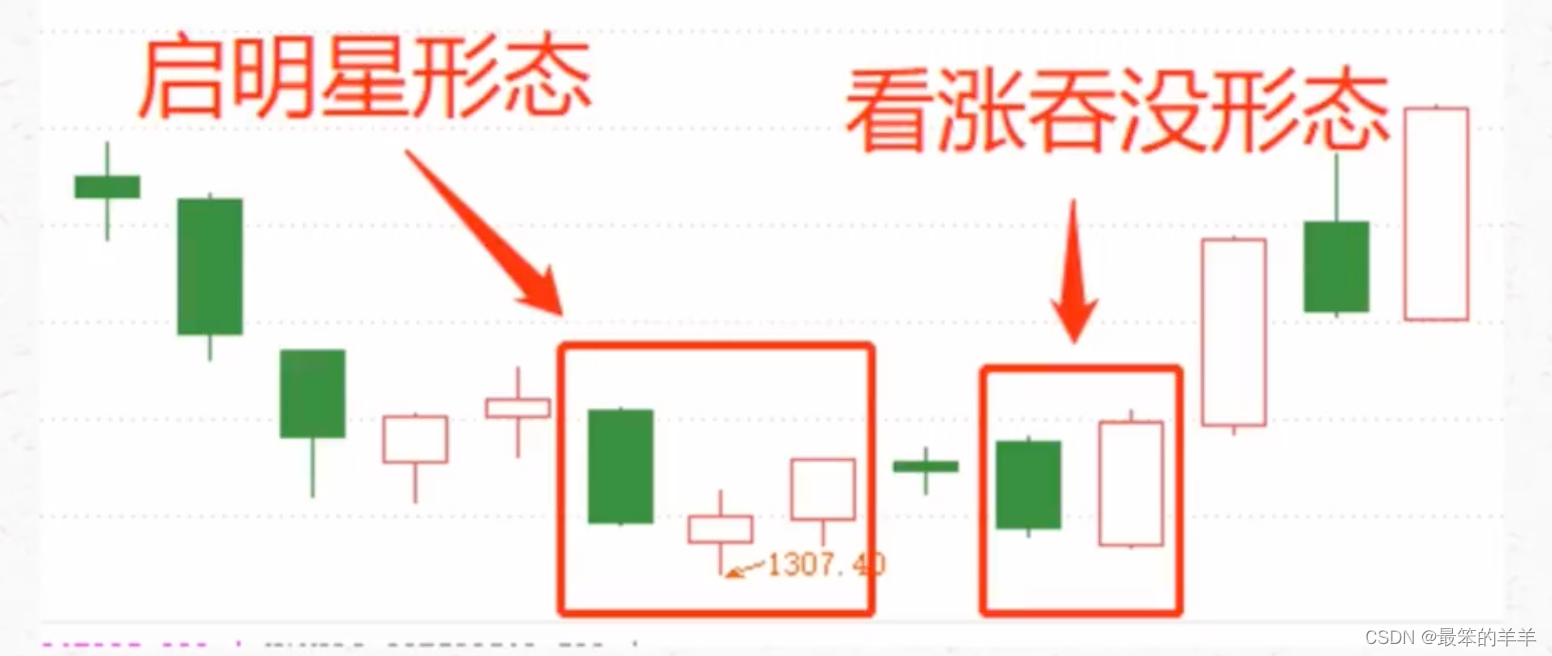
个股的日K图,一个启明星形态
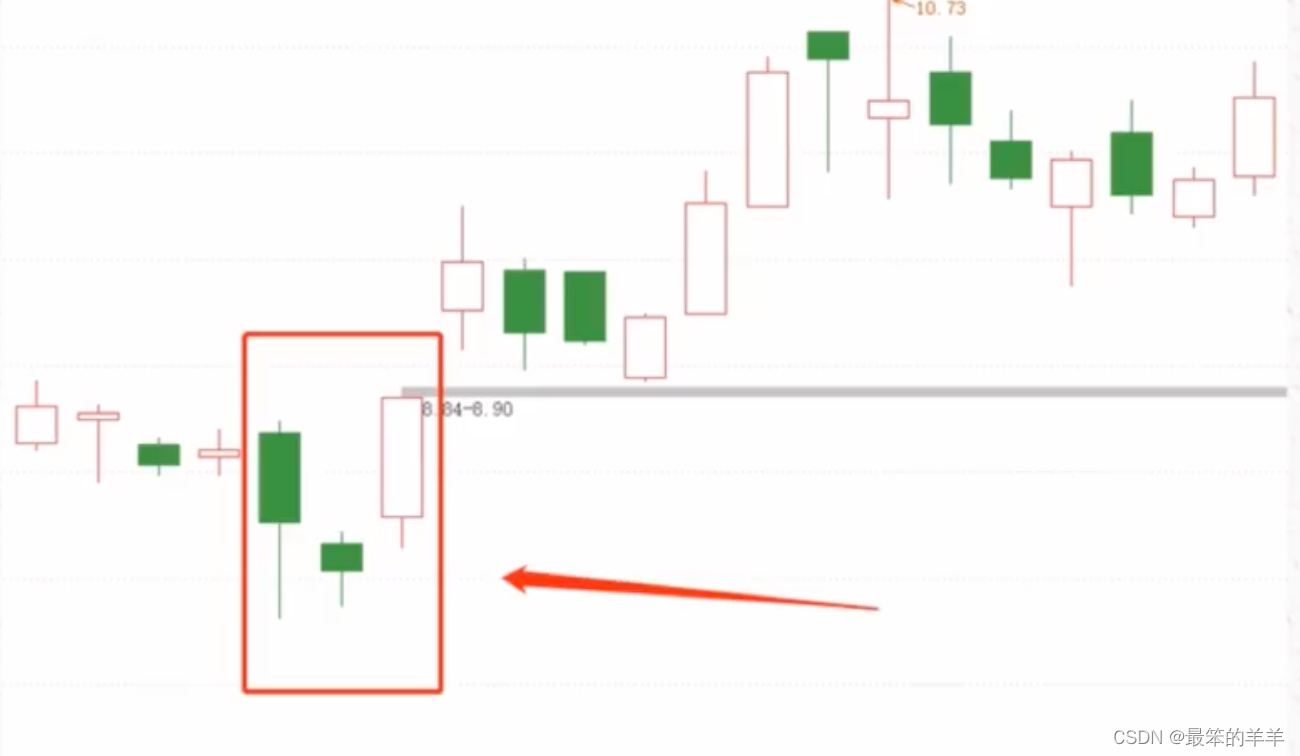
四、启明星形态的总结
- 这个组合由三根K线组成,出现在下降趋势中
- 第一根K线是一个较长的阴线,第二根K线上一根纺锤线,第三根K线是一根长阳线,实体部分要覆盖第一根阴线的大部分,覆盖的越多,反转信号越强
- 理想的启明星形态,中间的那根纺锤线的实体,与前后两根K线的实体都不重叠,存在跳空
- 正是因为这个纺锤线的实体,与前一根K线的实体存在价格跳空,才称之为星线,就像一颗空中挂着的星星
- 非理想形态的启明星形态,在行情底部出现,也具备一定的反转信号