【YOLO v5 v7 v8 小目标改进】归一化高斯 Wasserstein 距离（NWD损失函数）

归一化高斯 Wasserstein 距离（NWD损失函数）

提出背景
归一化Wasserstein距离
效果

YOLO v5 小目标改进
YOLO v7 小目标改进
YOLO v8 小目标改进

提出背景

论文：https://arxiv.org/pdf/2110.13389.pdf

代码：https://github.com/jwwangchn/NWD

由于摄像头距离人群较远，人们在图像中的尺寸非常小，可能小于16×16像素，这些微小的人群实例就成为了微小物体。

使用传统的IoU度量方法，如果一个人的检测框由于算法的轻微位置偏差而与实际位置有所不同，即使这种偏差很小（比如几个像素），也会导致IoU值急剧下降。

例如，对于一个6×6像素的微小人物，原本与真实框有一定重叠的检测框，仅因轻微的位置移动就可能从IoU为0.53下降到0.06，这样的变化会误导模型认为检测框与真实框不匹配，从而将其判定为负样本，导致正确的检测被错误地抑制。

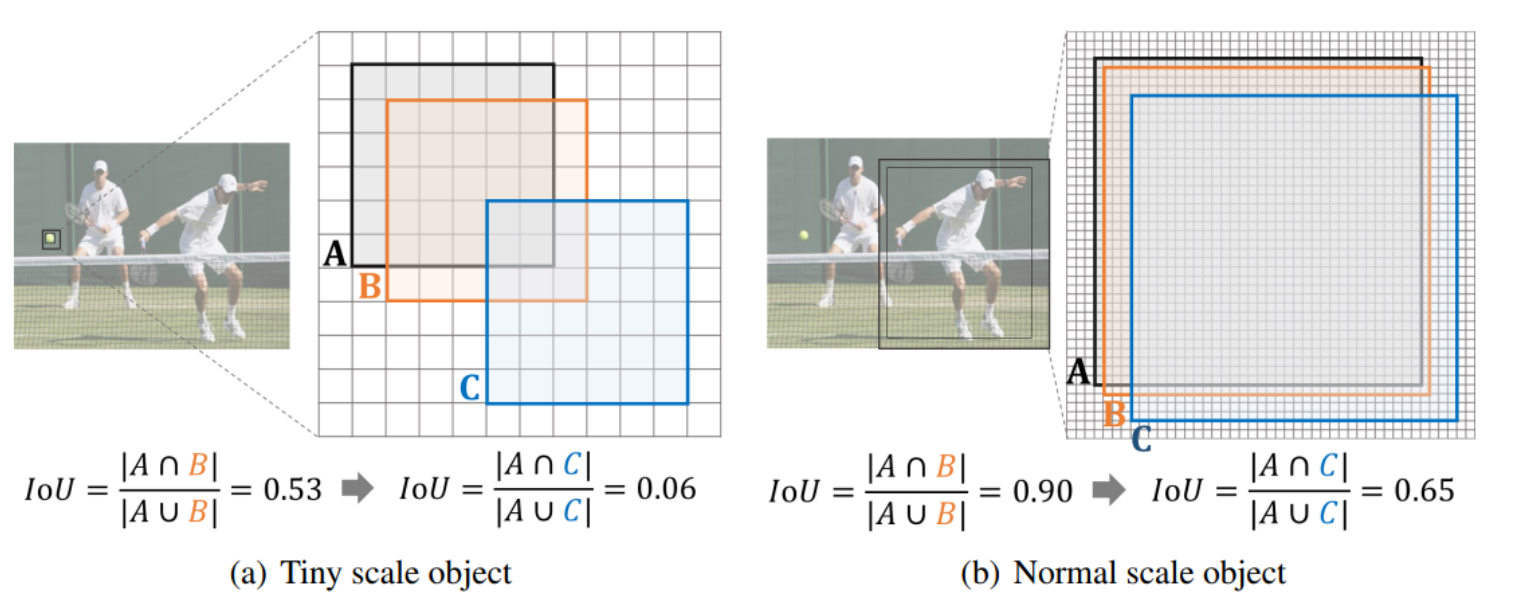
在这里插入图片描述
上图一个是微小尺度物体，另一个是正常尺度物体，突出了小的偏差如何导致微小物体的IoU显著下降，而对较大物体则没有这种情况。

为了解决这个问题，我们采用归一化Wasserstein距离（NWD）作为新的相似度度量方法。

具体来说，我们首先将每个检测框和真实框建模为2-D高斯分布。

这样，即使检测框和真实框之间的直接重叠很小或没有重叠，通过计算它们作为高斯分布的NWD，我们也能有效评估它们之间的相似度。

假设一个微小的人物实例的真实框和检测框都被建模为高斯分布。

真实框的中心位于图像中的(100,100)位置，检测框的中心因轻微的位置偏差位于(102,102)。

尽管这个位置偏差导致基于IoU的方法将检测框判定为低质量匹配，但通过计算这两个高斯分布之间的NWD，我们可以得出这两个框实际上是非常相似的，因为Wasserstein距离能够捕捉到它们作为分布的整体形状和位置的相似性，而不仅仅是它们的直接重叠区域。

因此，使用NWD，模型能够正确识别和保留这种轻微偏差的检测结果，从而提高微小物体检测的准确性和鲁棒性。

归一化Wasserstein距离

归一化Wasserstein距离 = 高斯分布建模 (为边界框提供更合适的空间表示) + Wasserstein距离 (量化两个分布之间的差异) + 归一化处理 (将距离转换为相似度度量)

将边界框建模为高斯分布，反映其空间特性。
使用Wasserstein距离计算两个高斯分布的差异。

传统的IoU度量在物体边界框不重叠或大小差异很大时效果不佳。

Wasserstein距离即使在没有重叠的情况下也能反映分布之间的距离。
归一化处理，将Wasserstein距离转换为0到1之间的相似度度量。
原因: 微小物体检测中，传统IoU表现不佳，需要一种能够处理空间偏差和尺寸差异的新方法。

下面公式描述在物体检测中，将边界框建模为高斯分布，并通过归一化的高斯Wasserstein距离（NWD）计算这些分布之间的相似性。

高斯分布建模：
- 定义边界框：对于边界框 $R = (c_x, c_y, w, h)$ ，其中 $c_x, c_y)$ 是中心坐标，( w ) 和 ( h ) 分别是宽度和高度。
- 描述其内接椭圆的方程： $\frac{(x - \mu_x)^2}{\sigma_x^2} + \frac{(y - \mu_y)^2}{\sigma_y^2} = 1$ ，其中 $\mu_x = c_x, \mu_y = c_y$ 是椭圆中心， $\sigma_x = \frac{w}{2}, \sigma_y = \frac{h}{2}$ 是沿着 ( x ) 轴和 ( y ) 轴的半轴长度。
- 2D高斯分布的概率密度函数： $f(x|\mu, \Sigma) = \frac{\exp\left(-\frac{1}{2}(x - \mu)^T\Sigma^{-1}(x - \mu)\right)}{2\pi|\Sigma|^{1/2}}$ ，其中 ( x ) 是坐标， $\mu$ 是均值向量， $\Sigma$ 是协方差矩阵。
归一化高斯Wasserstein距离：
- 定义2D高斯分布之间的Wasserstein距离： $W^2_2(\mu_1, \mu_2) = \|m_1 - m_2\|^2_2 + Tr\left[\Sigma_1 + \Sigma_2 - 2\left(\Sigma^{1/2}_2 \Sigma_1 \Sigma^{1/2}_2\right)^{1/2}\right]$ 。
- 将上述公式简化为Frobenius范数形式： $W^2_2(\mu_1, \mu_2) = \|m_1 - m_2\|^2_2 + \left\|\Sigma^{1/2}_1 - \Sigma^{1/2}_2\right\|^2_F$ 。
- 对于来自边界框A和B的高斯分布 $N_a, N_b$ ，进一步简化： $W^2_2(N_a, N_b) = \left\| \left[ \begin{array}{c} c_{xa} \\ c_{ya} \\ \frac{w_a}{2} \\ \frac{h_a}{2} \end{array} \right] - \left[ \begin{array}{c} c_{xb} \\ c_{yb} \\ \frac{w_b}{2} \\ \frac{h_b}{2} \end{array} \right] \right\|^2_2$ 。
- 归一化形式的NWD： $NWD(N_a, N_b) = \exp\left( -\sqrt{\frac{W^2_2(N_a, N_b)}{C}} \right)$ ，其中 ( C ) 是与数据集密切相关的常数。

通过这个流程，我们可以理解如何将物体检测中的边界框通过高斯分布进行建模，并计算它们之间的归一化Wasserstein距离来作为一种新的相似度度量方法。

效果

这种方法被证明在处理微小物体的检测任务时，尤其是在这些物体的边界框不重叠或大小差异很大时，优于传统的IoU度量方法。

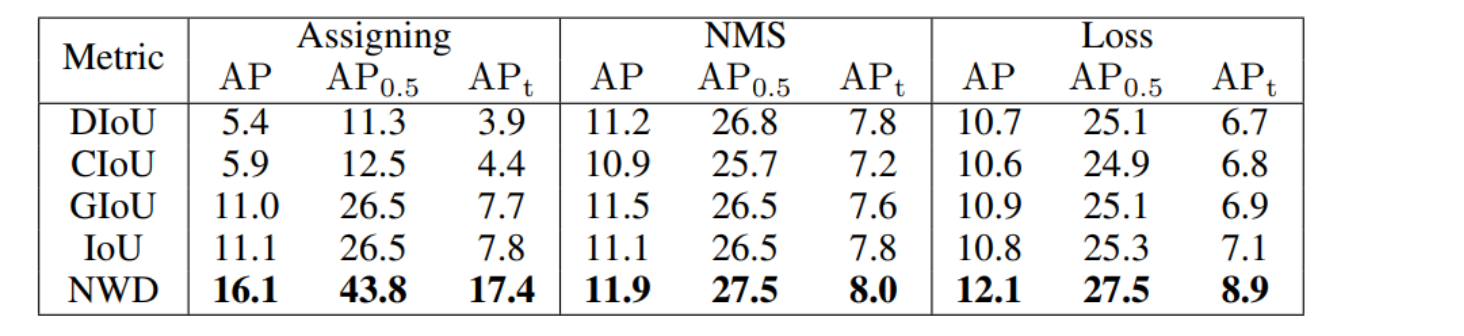
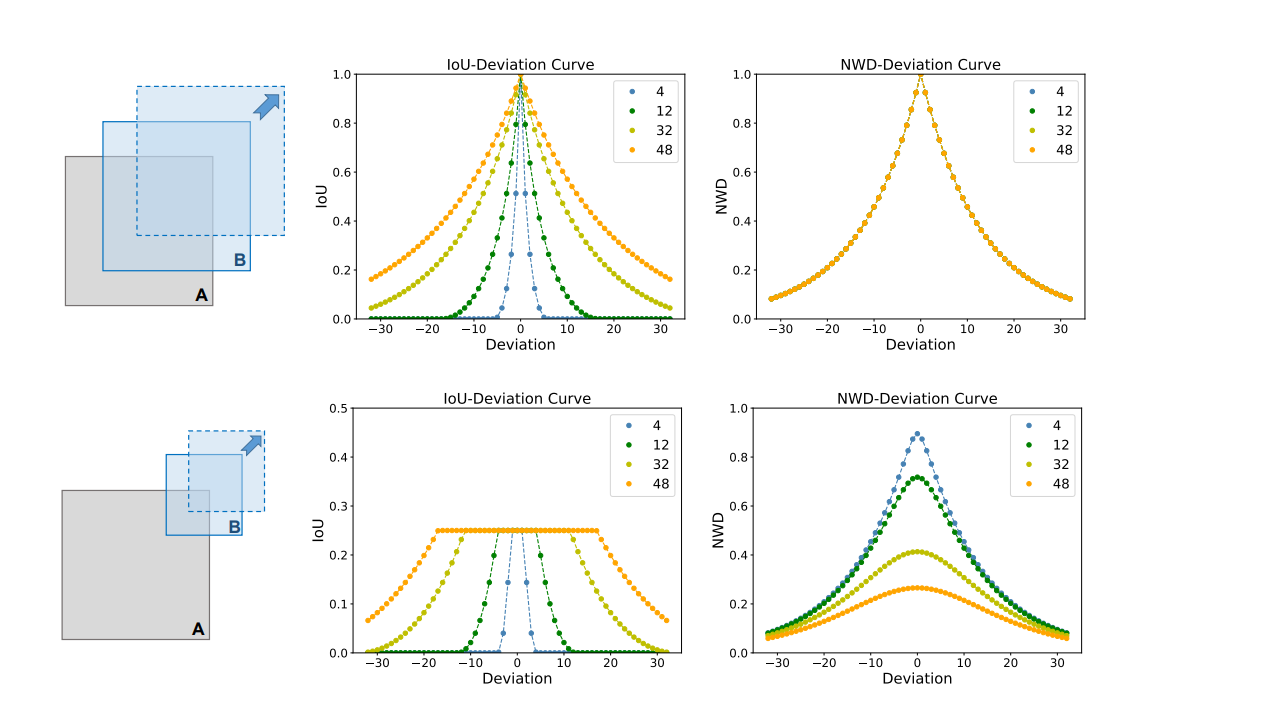
在这里插入图片描述

在这里插入图片描述
NWD度量对偏差的敏感性似乎较低，表明在不同物体尺度上性能更为平滑和一致。

YOLO v5 小目标改进

替换 ComputeLoss：

yolov5/utils/loss.py

import torch
import torch.nn as nn
from utils.general import bbox_iou  # 用于计算IoUclass ComputeLoss:# 初始化损失计算类def __init__(self, model, autobalance=False):self.sort_obj_iou = False  # 是否对对象的IoU进行排序device = next(model.parameters()).device  # 获取模型参数的设备类型h = model.hyp  # 获取超参数# 定义类别和对象存在性的二元交叉熵损失函数BCEcls = nn.BCEWithLogitsLoss(pos_weight=torch.tensor([h['cls_pw']], device=device))BCEobj = nn.BCEWithLogitsLoss(pos_weight=torch.tensor([h['obj_pw']], device=device))# 应用标签平滑self.cp, self.cn = smooth_BCE(eps=h.get('label_smoothing', 0.0))# 应用焦点损失g = h['fl_gamma']if g > 0:BCEcls, BCEobj = FocalLoss(BCEcls, g), FocalLoss(BCEobj, g)det = model.model[-1] if hasattr(model, 'model') else model[-1]  # 获取模型的Detect层# 根据层数调整平衡系数self.balance = {3: [4.0, 1.0, 0.4]}.get(det.nl, [4.0, 1.0, 0.25, 0.06, 0.02])self.ssi = list(det.stride).index(16) if autobalance else 0  # 如果自动平衡，获取步长为16的索引# 将初始化的变量赋值给实例self.BCEcls, self.BCEobj, self.gr, self.hyp, self.autobalance = BCEcls, BCEobj, 1.0, h, autobalancefor k in 'na', 'nc', 'nl', 'anchors':setattr(self, k, getattr(det, k))def __call__(self, p, targets):device = targets.device# 初始化分类、框和对象存在性损失lcls, lbox, lobj = torch.zeros(1, device=device), torch.zeros(1, device=device), torch.zeros(1, device=device)# 构建目标tcls, tbox, indices, anchors = self.build_targets(p, targets)# 计算损失for i, pi in enumerate(p):b, a, gj, gi = indices[i]tobj = torch.zeros_like(pi[..., 0], device=device)  # 目标对象存在性张量n = b.shape[0]  # 目标数量if n:# 获取与目标对应的预测子集ps = pi[b, a, gj, gi]# 回归损失pxy = ps[:, :2].sigmoid() * 2 - 0.5pwh = (ps[:, 2:4].sigmoid() * 2) ** 2 * anchors[i]pbox = torch.cat((pxy, pwh), 1)  # 预测的框# 计算IoU和Wasserstein距离iou = bbox_iou(pbox.T, tbox[i], x1y1x2y2=False, CIoU=True)wasserstein = calculate_nwd(pbox, tbox[i])  # 计算NWD# 组合IoU和Wasserstein损失lbox += 0.9 * (1.0 - iou).mean() + 0.1 * (1.0 - wasserstein).mean()# 对象存在性损失score_iou = iou.detach().clamp(0).type(tobj.dtype)if self.sort_obj_iou:sort_id = torch.argsort(score_iou)b, a, gj, gi, score_iou = b[sort_id], a[sort_id], gj[sort_id], gi[sort_id], score_iou[sort_id]tobj[b, a, gj, gi] = (1.0 - self.gr) + self.gr * score_iou  # 分配对象存在性分数# 分类损失if self.nc > 1:t = torch.full_like(ps[:, 5:], self.cn, device=device)  # 目标t[range(n), tcls[i]] = self.cplcls += self.BCEcls(ps[:, 5:], t)  # 二元交叉熵损失obji = self.BCEobj(pi[..., 4], tobj)lobj += obji * self.balance[i]  # 对象存在性损失if self.autobalance:self.balance[i] = self.balance[i] * 0.9999 + 0.0001 / obji.detach().item()if self.autobalance:self.balance = [x / self.balance[self.ssi] for x in self.balance]lbox *= self.hyp['box']lobj *= self.hyp['obj']lcls *= self.hyp['cls']bs = tobj.shape[0]  # 批量大小return (lbox + lobj + lcls) * bs, torch.cat((lbox, lobj, lcls)).detach()def build_targets(self, p, targets):# 为compute_loss()构建目标，输入targets格式为(image,class,x,y,w,h)na, nt = self.na, targets.shape[0]  # 锚点数量，目标数量tcls, tbox, indices, anch = [], [], [], []  # 初始化分类目标，框目标，索引，锚点列表gain = torch.ones(7, device=targets.device)  # 归一化到网格空间的增益ai = torch.arange(na, device=targets.device).float().view(na, 1).repeat(1, nt)  # 与.repeat_interleave(nt)相同targets = torch.cat((targets.repeat(na, 1, 1), ai[:, :, None]), 2)  # 添加锚点索引g = 0.5  # 偏移量off = torch.tensor([[0, 0],  # 定义偏移量，用于微调目标位置[1, 0], [0, 1], [-1, 0], [0, -1]],  # j,k,l,mdevice=targets.device).float() * g  # 偏移量for i in range(self.nl):  # 遍历每个预测层anchors = self.anchors[i]  # 当前层的锚点gain[2:6] = torch.tensor(p[i].shape)[[3, 2, 3, 2]]  # xyxy增益# 将目标匹配到锚点t = targets * gain  # 调整目标到当前层的尺寸if nt:# 匹配r = t[:, :, 4:6] / anchors[:, None]  # 宽高比j = torch.max(r, 1 / r).max(2)[0] < self.hyp['anchor_t']  # 比较宽高比，选择最佳匹配的锚点t = t[j]  # 筛选# 应用偏移量gxy = t[:, 2:4]  # 网格xygxi = gain[[2, 3]] - gxy  # 反向偏移j, k = ((gxy % 1 < g) & (gxy > 1)).T  # 根据偏移量微调位置l, m = ((gxi % 1 < g) & (gxi > 1)).Tj = torch.stack((torch.ones_like(j), j, k, l, m))t = t.repeat((5, 1, 1))[j]offsets = (torch.zeros_like(gxy)[None] + off[:, None])[j]else:t = targets[0]offsets = 0# 定义b, c = t[:, :2].long().T  # 图片编号，类别gxy = t[:, 2:4]  # 网格xygwh = t[:, 4:6]  # 网格whgij = (gxy - offsets).long()gi, gj = gij.T  # 网格xy索引# 添加到列表a = t[:, 6].long()  # 锚点索引indices.append((b, a, gj.clamp_(0, gain[3] - 1), gi.clamp_(0, gain[2] - 1)))  # 添加图片编号，锚点索引，网格索引tbox.append(torch.cat((gxy - gij, gwh), 1))  # 添加框anch.append(anchors[a])  # 添加锚点tcls.append(c)  # 添加类别return tcls, tbox, indices, anch  # 返回分类目标，框目标，索引，锚点

YOLO v7 小目标改进

YOLO v8 小目标改进

在 loss.py 下的：

class BboxLoss(nn.Module):iou = bbox_iou(pred_bboxes[fg_mask], target_bboxes[fg_mask], xywh=False, CIoU=True)loss_iou = ((1.0 - iou) * weight).sum() / target_scores_sum

替换成：

class BboxLoss(nn.Module):# ... [假设其他部分的代码保持不变] ...def forward(self, pred_boxes, true_boxes, fg_mask, target_scores):# 计算预测框和真实框之间的IOUiou_loss = bbox_iou(pred_boxes[fg_mask], true_boxes[fg_mask], xywh=False, CIoU=True)# 分解预测框和真实框的坐标pred_xmin, pred_ymin, pred_xmax, pred_ymax = pred_boxes[fg_mask].unbind(-1)true_xmin, true_ymin, true_xmax, true_ymax = true_boxes[fg_mask].unbind(-1)# 计算预测框和真实框中心点的L2距离distance_x = torch.pow((pred_xmin - true_xmin), 2)distance_y = torch.pow((pred_ymin - true_ymin), 2)p1_distance = distance_x + distance_y# 计算预测框和真实框宽高的Frobenius范数width_diff = torch.pow((pred_xmax - true_xmax)/2, 2)height_diff = torch.pow((pred_ymax - true_ymax)/2, 2)p2_distance = width_diff + height_diff# 计算标准化高斯Wasserstein距离wasserstein_dist = torch.exp(-torch.pow((p1_distance + p2_distance), 1 / 2) / 2.5)# 根据选择使用NWD损失或默认v8损失use_wd_loss = True # True 使用 NWD 损失, False 使用默认的 v8 损失if use_wd_loss:# 计算组合损失，结合IOU损失和Wasserstein距离损失combined_loss = (0.7 * ((1.0 - iou_loss) * target_scores).sum() + 0.3 * ((1.0 - wasserstein_dist) * target_scores).sum()) / target_scores.sum()else:# 只使用IOU损失combined_loss = ((1.0 - iou_loss) * target_scores).sum() / target_scores.sum()return combined_loss