主要参考资料：
还没搞懂嵌入（Embedding）、微调（Fine-tuning）和提示工程（Prompt Engineering）？: https://blog.csdn.net/DynmicResource/article/details/133638079
B站Up主Nenly同学《60分钟速通LORA训练！》

提示工程（Prompt Engineering）

如果没有良好的提示设计和基础技术，模型很可能产生幻觉或编造答案，其危险在于，模型往往会产生非常有说服力和看似合理的答案，因此必须非常小心地设计安全缓解措施和地面模型的事实答案，所以提示工程应运而生。

微调（Fine-tuning）

微调通过训练比提示(prompt)中更多的示例来改进小样本学习，让您在大量任务中取得更好的结果。对模型进行微调后，您将不再需要在提示(prompt)中提供示例。这样可以节省成本并实现更低延迟的请求。
下面是Nvidia Inception大会上的两张图。微调大致可以分为参数优化微调（Parameter Efficient Fine Tuning）和全量微调（Fine Tuning），典型的就是LoRA方法和SFT。

LoRA微调

模型权重：在深度学习中，模型的权重（Weights）是指神经网络中的参数。这些参数用于调整和学习模型的行为。而参数的存储方式就是矩阵。

LoRA做了两件事：
（1）"冻结"了原来的权重，在旁边另起了一个单独的“微调权重”来进行训练。

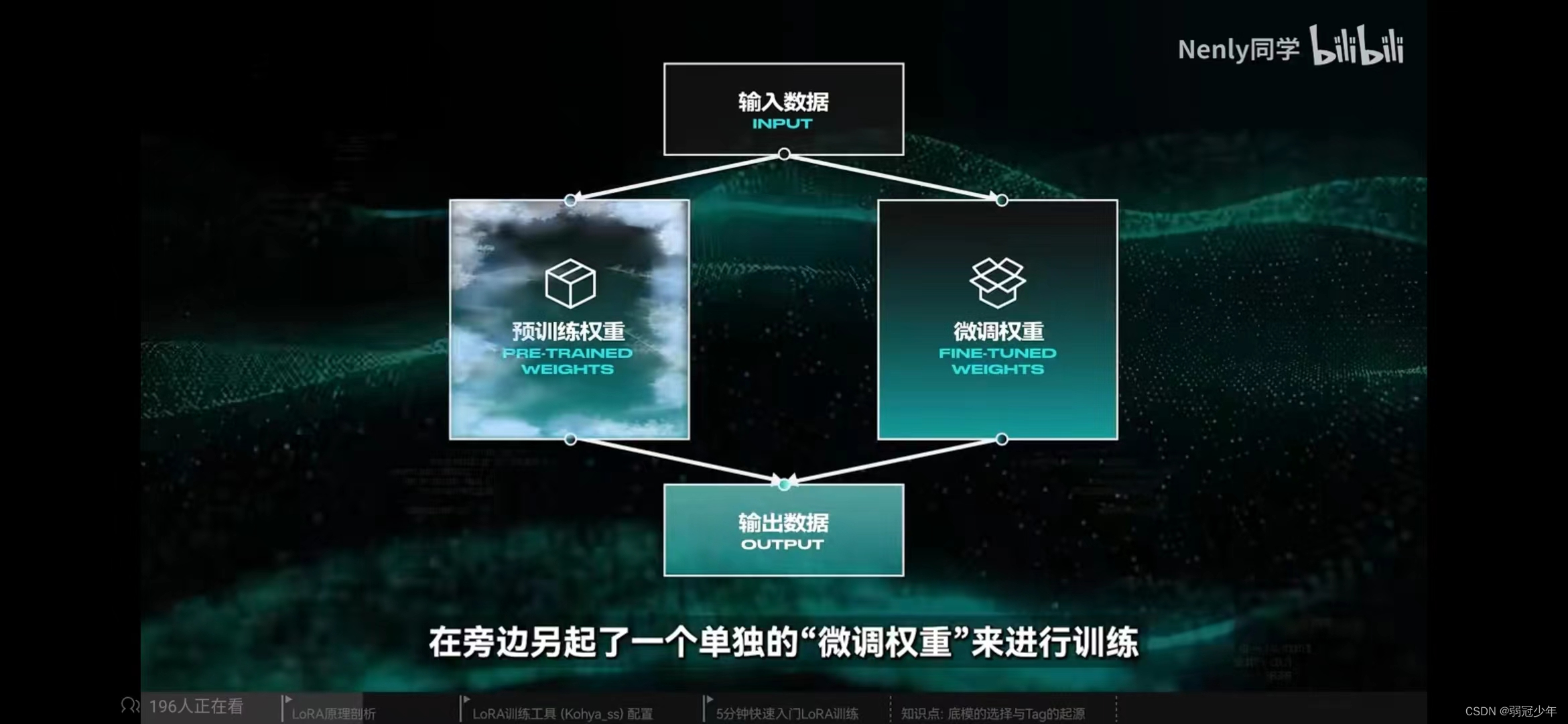
（2）“降本增效”。主要参考资料里的微软论文研究发现，微调前2行2列的效果与等于计算全部行列（LoRA有两个转换器，一个是把“满秩”转换为“低秩”，方便微调，另一个再将“低秩”转换为“满秩”。矩阵的“秩”是线性代数的一个概念，描述了这个矩阵的信息丰富度和多样性。）

嵌入（Embedding）