此示例演示如何使用 polyint 和 polyder 函数对由系数向量表示的任何多项式求解析积分或微分。

        使用 polyder 获取多项式 p(x)=x^3−2x−5 的导数。生成的多项式为

p = [1 0 -2 -5];
q = polyder(p)
q = 1×33     0    -2

        同样，使用 polyint 对多项式 p(x)=4x^3−3x^2+1 求积分。生成的多项式为

p = [4 -3 0 1];
q = polyint(p)
q = 1×51    -1     0     1     0

        polyder 也可以计算两个多项式积或商的导数。例如，创建两个向量来表示多项式

a = [1 3 5];
b = [2 4 6];

        通过调用带有单个输出参数的 polyder 来计算导数

c = polyder(a,b)
c = 1×48    30    56    38

        通过调用带有两个输出参数的 polyder 来计算导数。生成的多项式为

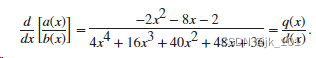
[q,d] = polyder(a,b)
q = 1×3-2    -8    -2d = 1×54    16    40    48    36