目录
- 介绍
- 集合论与映射
- 映射相关定义
- 映射(map)
- 映射的一种分类:一一的和到上的
- 拓扑空间
- 背景介绍
- 开子集
- 开子集的选择
- 拓扑
- 拓扑空间
- 常见拓扑
- 拓扑子空间
- 同胚
- 其他重要定义
- 开覆盖
- 紧致性
- 有限开覆盖
- 紧致性
- R R R的紧致性
- 习题
介绍
这是对梁灿彬的《微分几何与广义相对论》一书的阅读记录,对微分几何这种比较复杂的数学理论没经过在学校大量练习,还不做一些笔记,是难以熟悉掌握的。这里会结合我自身的知识储备,记录下微分几何的知识递进脉络。
集合论与映射
只需要了解过高中和大学掌握的朴素集合论,就可以进入微分几何的学习,这里不做阐述。
映射相关定义
映射也是高中就涉及到的知识,但它的具体定义在高数题目中其实很少用到,感觉不太熟悉这一方面,这里列出书上给出的严格定义。
映射(map)
定义:设 X X X, Y Y Y是非空集合,一个从 X X X到 Y Y Y的映射(map),记作 f : X → Y f: X\rightarrow Y f:X→Y,是一个法则 f f f,它给 X X X中每个元素,指定 Y Y Y中唯一的对应元素。若 y ∈ Y y\in Y y∈Y是 x ∈ X x\in X x∈X的对应元素,写作 y = f ( x ) y=f(x) y=f(x),称 y y y为 x x x在映射 f f f下的像(image),称 x x x为 y y y的原像或逆像(inverse image)。 X X X称为映射 f f f的定义域(domain), X X X的所有元素在映射 f f f下的像的集合,记作 f [ X ] f[X] f[X],称为映射 f : X → Y f:X\rightarrow Y f:X→Y的值域(range)。
以下给出一些常用记法和说明:
- 映射的相等:当且仅当 f ( x ) = f ′ ( x ) , ∀ x ∈ X f(x)=f'(x),\forall x\in X f(x)=f′(x),∀x∈X,映射 f : X → Y f: X\rightarrow Y f:X→Y和映射 f ′ : X → Y f': X\rightarrow Y f′:X→Y相等。
- y = f ( x ) y=f(x) y=f(x)的另一种记法为: f : x ↦ y f:x\mapsto y f:x↦y
- 在映射 f f f下部分像的集合,可以记为 f [ A ] = { y ∈ Y ∣ ∃ x ∈ A , y = f ( x ) } ⊂ Y f[A]=\{y\in Y| \exists x\in A, y=f(x)\}\subset Y f[A]={y∈Y∣∃x∈A,y=f(x)}⊂Y
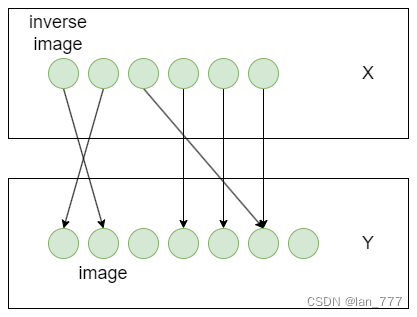
上图是映射的简单示意图,可以加深印象,认识到 X X X中每个元素都会映射到 Y Y Y,形象化的说就是 X X X中每个元素都会伸出一个箭头到 Y Y Y中某元素上;但 Y Y Y中的元素则没有什么严格约束,可以多个箭头连到一个元素上,也可以有没有箭头连的“孤独的元素”。
映射的一种分类:一一的和到上的
定义: 映射 f : X → Y f:X\to Y f:X→Y是一一的(one-to-one),当且仅当任意一个 y ∈ Y y\in Y y∈Y,有不多于一个原像; f : X → Y f:X\to Y f:X→Y是到上的(onto),当且仅当任意一个 y ∈ Y y\in Y y∈Y都有原像。
这里是梁书中的叫法,其他书中有用单射(injection)和满射(surjection)的,它们对应上述定义的一一和到上。
既是一一的又是到上的映射被称为一一到上的,其他书中可能称为双射(bijection)或一一映射,这种一一映射会强于之前定义的一一的。为避免歧义,一一的仅用于指单射。
单射和满射的概念很简单,但不经常锻炼又容易混淆,这里从名字上来速记。单射和满射都是针对 Y Y Y的约束,单射中的单对应至多1个,意思是 Y Y Y中元素被至多一个箭头指向;满射中的满对应所有,即所有 Y Y Y中的元素都有箭头指向它。
拓扑空间
背景介绍
如果映射 f : X → Y f:X\to Y f:X→Y中, X = R X=R X=R且 Y = R Y=R Y=R,那么 f f f就表示定义域为 R R R的一元函数。这个映射不仅可以定义一一到上的要求,还可以定义连续性,可微性等诸多有用的属性。高等数学中对连续性的定义依赖于距离这个概念:
∀ ε > 0 , ∃ δ > 0 , w h e n ∣ x ′ − x ∣ < δ , ∣ f ( x ′ ) − f ( x ) ∣ < ε \forall\varepsilon>0, \exist \delta>0,when\ |x'-x|<\delta, |f(x')-f(x)|<\varepsilon ∀ε>0,∃δ>0,when ∣x′−x∣<δ,∣f(x′)−f(x)∣<ε
这里,两个不等式实质上都是暗示数轴上的距离大小关系相互依赖。只有距离能定义,这种连续性才可以定义,这肯定无法推广到任意集合上,因为有些集合无法定义出距离。
然而,细想一下,似乎连续性有另一种不依赖于距离的定义方式,即:使用开区间定义,描述如下:
设 X = Y = R X=Y=R X=Y=R,当且仅当 Y Y Y中任一开区间的“逆像”都是 X X X的开区间之并(或空集), f : X → Y f:X\to Y f:X→Y是连续的。
不给出证明,只考虑一下这个定义能不能去排除间断点即可。
- 对于可去间断点,在那个间断点附近取 Y Y Y的一个很小的开区间,逆像将只有一个元素,一个元素显然不可能是开区间,也不可能表示为开区间之并,因此背离定义,是不连续的。
- 对于跳跃间断点,在跳跃点总能取到一个开区间,让原像包含一端闭区间,只要有一端是闭区间,就不可能表示为开区间之并。
- 对于无穷间断点,补充定义的话,只要包含定义的点,那么原像就包含闭区间。
- 对于震荡间断点,同样在无定义点补充定义的话,那么原像也要包含一个只有一个元素的区间,其他开区间将无限趋近于这个点。
开子集
上述开区间之并的概念很重要,不仅可以用于定义连续性,还可以推广到任意集合。 R R R的可表示为开区间之并的子集我们称为开子集。我们将开子集的概念进行推广。
开子集的选择
在 R R R上有天然的开子集定义,使用开区间来定义即可。但对于任意集合,可能都不存在数轴的概念,无法定义开区间,我们则需要指定一种开子集的定义方式。同一集合可以定义多种开子集,我们先对定义方式做出约束,即开子集需要满足的基本性质:
- X X X集本身和空集 ∅ \varnothing ∅为开子集
- 有限个开子集之交为开子集
- 任意个开子集之并为开子集
可见,只定义 ∅ \varnothing ∅和 X X X为开子集,其他子集都不是开子集,这就是一种开子集的定义方式;指定 X X X的所有子集都是开子集也是一种定义方式。只不过这两种定义方式都是比较平凡的,除了满足性质外,没有对集合 X X X附加什么约束。
拓扑
当我们为一个集合 X X X定义了一种开子集,就是为 X X X附加了一种额外结构,即拓扑结构。
定义了拓扑结构的集合 X X X的全体开子集的集合,被称为 X X X的一个拓扑。书上将一个拓扑用花体符号来写,笔记里就简单记录为 T T T。
更符号化的写法是:非空集合 X X X的一个拓扑(topology) T T T是 X X X的若干子集的集合,满足:
- X ∈ T , ∅ ∈ T X\in T, \varnothing\in T X∈T,∅∈T
- 若 O i ∈ T O_i\in T Oi∈T, i = 1 , 2 , ⋯ , n i=1,2,\cdots,n i=1,2,⋯,n,则 ⋂ n i = 1 O i ∈ T \underset{i=1}{\overset{n}\bigcap}O_i\in T i=1⋂nOi∈T
- 若 O α ∈ T , ∀ α O_\alpha\in T, \forall \alpha Oα∈T,∀α,则 ⋂ α O α ∈ T \underset{\alpha}{\bigcap}O_\alpha\in T α⋂Oα∈T
拓扑空间
定义了拓扑 T T T的集合 X X X称为拓扑空间,记为 ( X , T ) (X,T) (X,T),明确了拓扑时,也可只记为 X X X。
常见拓扑
- 离散拓扑:指定 X X X中所有子集为开子集所定义的拓扑。
- 凝聚拓扑:只指定 X X X和 ∅ \varnothing ∅为开子集所定义的拓扑。
- R R R的通常拓扑:指定 ∅ \varnothing ∅或 R R R中能表示为开区间之并的子集为开子集所定义的拓扑。
- R n R^n Rn的通常拓扑:指定 ∅ \varnothing ∅或 R n R^n Rn中能表示为开球之并的子集为开子集所定义的拓扑。其中开球是集合 B ( x 0 , r ) = { x ∈ R n ∣ ∣ x − x 0 ∣ < r } B(x_0,r)=\{x\in R^n|\ |x-x_0|<r\} B(x0,r)={x∈Rn∣ ∣x−x0∣<r},可以发现 n = 1 n=1 n=1时,开球就是开区间。
- 乘积拓扑:设两个拓扑空间 ( X 1 , T 1 ) (X_1, T_1) (X1,T1)和 ( X 2 , T 2 ) (X_2, T_2) (X2,T2), X = X 1 × X 2 X=X_1\times X_2 X=X1×X2(笛卡尔积),定义 X X X的拓扑为: T = { O ∈ X ∣ O T=\{O\in X | O T={O∈X∣O可表示为形如 O 1 × O 2 O_1\times O_2 O1×O2的子集之并, O 1 ∈ T 1 , O 2 ∈ T 2 } O_1\in T_1, O_2\in T_2\} O1∈T1,O2∈T2},乘积拓扑可以推广到 n n n个拓扑的乘积, R n R^n Rn就是 R R R的乘积拓扑。
拓扑子空间
对于拓扑空间 ( X , T ) (X,T) (X,T)来说, X X X有一个非空子集 A A A, A A A也可指定一个拓扑 T S T_S TS,使得 A A A也成为拓扑空间。
如果 A ∈ T A\in T A∈T,即 A A A是 X X X在拓扑 T T T下的开子集,那么 T S T_S TS很好定义,只要定义 T S = { V ⊂ A ∣ V ∈ T } T_S=\{V\subset A | V\in T\} TS={V⊂A∣V∈T},即 A A A的所有子集中,属于 T T T的那些,都定义为 A A A的开子集即可。然而如果 A A A不是 X X X的开子集,那么按照上述 T S T_S TS的定义, A ∉ T S A\notin T_S A∈/TS,这违背了拓扑空间的定义。
一个更巧妙的 T S T_S TS的定义是:
T S = { V ⊂ A ∣ ∃ O ∈ T , V = A ∩ O } T_S=\{V\subset A | \exist O\in T, V=A\cap O\} TS={V⊂A∣∃O∈T,V=A∩O}
这样即使 A A A不是 X X X的开子集, T S T_S TS也满足拓扑的要求。 T S T_S TS叫做 A A A的、由 T T T导出的诱导拓扑, ( A , T S ) (A,T_S) (A,TS)称为 ( X , T ) (X,T) (X,T)的拓扑子空间。
诱导拓扑是一个比较抽象的概念,书上举了一个很好的例子加深理解, R 2 R^2 R2上的通常拓扑是一个个开圆盘的并,在 R 2 R^2 R2中随便找一个圆周,它肯定不是开子集,但它上面也可以定义拓扑,就是用开圆盘和圆周相交,交的结果作为圆周的开子集。
这里我加入一些个人的理解,按开子集是开区间的抽象,是对集合的几何性质的一种描述,我们取 R 2 R^2 R2上通常拓扑的情况下,很显然一个个开球或开球之并是开区间之并,但二维空间中的圆周它本身也是连续的,按理说在上面定义一个和 R 2 R^2 R2中开区间意义接近的开区间也不难,但它不符合 R 2 R^2 R2上的开区间定义,所以诱导拓扑就是弱化了拓扑的定义,从而方便在这样的几何形状上复用 R 2 R^2 R2的拓扑结构,而无需再定义一个额外的拓扑。
同胚
在拓扑空间中重新定义连续:设 ( X , T ) (X,T) (X,T)和 ( Y , T S ) (Y,T_S) (Y,TS)为拓扑空间,映射 f : X → Y f:X\to Y f:X→Y是连续的,当且仅当 f − 1 [ O ] ∈ T , ∀ O ∈ T S f^{-1}[O]\in T,\ \forall O\in T_S f−1[O]∈T, ∀O∈TS。
单点连续定义:设 ( X , T ) (X,T) (X,T)和 ( Y , T S ) (Y,T_S) (Y,TS)为拓扑空间,映射 f : X → Y f:X\to Y f:X→Y在 x ∈ X x\in X x∈X处连续,当且仅当对于 Y Y Y中任意包含 f ( x ) f(x) f(x)的开子集 G ′ G' G′,总存在 X X X的一个开子集 G G G,使得 x ∈ G x\in G x∈G且 f [ G ] ⊂ G ′ f[G]\subset G' f[G]⊂G′。(原书中符号表达是这样的: ∀ \forall ∀满足 f ( x ) ∈ G ′ f(x)\in G' f(x)∈G′的 G ′ ∈ T S G'\in T_S G′∈TS, ∃ G ∈ T \exist G\in T ∃G∈T使得 x ∈ G x\in G x∈G且 f [ G ] ⊂ G ′ f[G]\subset G' f[G]⊂G′)
同胚: ( X , T X ) (X,T_X) (X,TX)和 ( Y , T Y ) (Y,T_Y) (Y,TY)称为互相同胚的(homeomorphic to each other),当且仅当存在一个映射 f : X → Y f: X\to Y f:X→Y,满足:
- f f f是一一到上的;
- f f f和 f − 1 f^{-1} f−1都连续。
这样, f f f称为 ( X , T X ) (X,T_X) (X,TX)到 ( Y , T Y ) (Y,T_Y) (Y,TY)的同胚映射,简称同胚。
为什么同胚定义要求映射一一到上的,还要求 f f f和 f − 1 f^{-1} f−1都连续?按理说一一到上且 f f f连续,那么 f − 1 f^{-1} f−1就一定连续。实际上 R R R在通常拓扑下确实是这样,但这里是任意的拓扑。只需要将 T X T_X TX取为凝聚拓扑, T Y T_Y TY取为离散拓扑,那么 f f f连续, f − 1 f^{-1} f−1将大概率不连续,即使映射是一一到上的。
可微性可否推广?连续性可微性有一个通用的记法 C n C^n Cn,即 n n n阶导函数存在且连续。 C 0 C^0 C0就对应连续性, C ∞ C^\infty C∞对应光滑。 C 0 C^0 C0可以推广到拓扑空间的映射,但对于更高的要求则不能。事实上,拓扑空间之间的映射最高要求就是同胚,同胚在 X X X和 Y Y Y中元素之间建立了一一对应关系,且在开子集之间也建立了一一对应关系。一切由拓扑决定的性质会全息的被 f f f携带到 Y Y Y中,互相同胚的拓扑空间就是字面意义上像得不能再像了。
其他重要定义
这些定义其实在多元函数微积分中都存在,比如边界,内部,连通性等都能在 R 2 R^2 R2上的二元函数上找到对应的概念,事实上这些概念可以视为在拓扑上的延伸。
- 邻域:集合 N ⊂ X N\subset X N⊂X称为 x ∈ X x\in X x∈X的邻域,当且仅当 ∃ O ∈ T \exist O\in T ∃O∈T,使得 x ∈ O ⊂ N x\in O\subset N x∈O⊂N,自身是开集的邻域叫开邻域。简而言之,就是一个集合能视为邻域,它就必须包含一个开子集,且 x x x属于这个开子集。
- 闭集: C ⊂ X C\subset X C⊂X叫做闭集(closed set),当且仅当 − C ∈ T -C\in T −C∈T。形象说,就是 C C C的补集一定是开子集。闭集与开集完全对应,因此也满足3条性质,即“任意交、有限并、 X X X和 ∅ \varnothing ∅是闭集”
- 既开又闭:显然 X X X和 ∅ \varnothing ∅既是开集有是闭集,任何拓扑空间都有这两个既开又闭的子集。
- 连通的:只存在 X X X和 ∅ \varnothing ∅两个既开又闭的子集的拓扑空间是连通的。不连通的例子也好想,就 R R R上的两个不相交的开区间 A A A和 B B B,视为一个集合,由R的通常拓扑在这两个线段上诱导出的拓扑,就有两个额外的既开又闭的子集 A A A和 B B B。恰好这两个区域确实不连通。
- 闭包: A A A的闭包 A ˉ \bar{A} Aˉ是所有包含 A A A的闭集的交集。
- 内部: A A A的内部 i ( A ) i(A) i(A)是所有 A A A包含的开集的并集。
- 边界: A A A的边界是 A ∙ = A ˉ − i ( A ) \overset{\bullet}A=\bar{A}-i(A) A∙=Aˉ−i(A)
开覆盖
定义: X X X的开子集的集合 { O α } \{O_\alpha\} {Oα}叫做 A ⊂ X A\subset X A⊂X的一个开覆盖(open cover),当且仅当 A ⊂ ⋃ α O α A\subset \underset{\alpha}\bigcup O_\alpha A⊂α⋃Oα。也可称 { O α } \{O_\alpha\} {Oα}覆盖 A A A。
紧致性
有限开覆盖
设 { O α } \{O_\alpha\} {Oα}是 A ⊂ X A\subset X A⊂X的开覆盖,如果 { O α } \{O_\alpha\} {Oα}的有限元素的子集也覆盖 A A A,称 { O α } \{O_\alpha\} {Oα}有有限开覆盖。
紧致性
A A A的任一开覆盖都有有限开覆盖,则称 A A A为紧致的。
紧致性稍微难以从直观的角度理解,选用 R R R的通常拓扑举例,如果 A A A是单点集(只包含一个元素),那他肯定是紧致的,任一开覆盖都必定有一个元素,这个元素包含 A A A中的唯一点。
但 A A A只要包含开区间,哪怕是单边开区间, A A A就不会是紧致的。比如 A = ( 0 , 1 ] A=(0,1] A=(0,1],可以选择一个开覆盖: { ( 1 / n , 2 ) ∣ n ∈ N } \{(1/n,2)|n\in N\} {(1/n,2)∣n∈N},这一段段开子集(开区间)一段逐渐逼近 0 0 0,无限并则肯定可以覆盖 A A A,但没有任何一个有限的并可以覆盖 A A A。
R R R的紧致性
对于 R R R,有几个紧致性的结论, R R R本身不是紧致的; R R R的任意闭区间都紧致, R R R的任一开区间或半开区间都非紧致。
R R R的紧致性和闭集有密切联系,但不等价,具体区别可以归结为一个定理:
若 ( X , T ) (X,T) (X,T)为 T 2 T_2 T2空间, A ⊂ X A\subset X A⊂X为紧致的,则 A A A为闭集。
其中, T 2 T_2 T2空间又叫做豪斯多夫空间,它指的是满足以下性质的拓扑空间: ∀ x , y ∈ X , x ≠ y , ∃ O 1 , O 2 ∈ T \forall x,y\in X, x\neq y, \exists O_1,O_2\in T ∀x,y∈X,x=y,∃O1,O2∈T,使得 x ∈ O 1 , y ∈ O 2 x\in O_1, y\in O_2 x∈O1,y∈O2,且 O 1 ∩ O 2 = ∅ O_1\cap O_2=\varnothing O1∩O2=∅。
常见的拓扑空间都是 T 2 T_2 T2空间,但绝非全部。
习题
- 试证 A − B = A ∩ ( X − B ) , ∀ A , B ⊂ X A-B=A\cap(X-B), \forall A,B\subset X A−B=A∩(X−B),∀A,B⊂X.
只要列举出差集的定义即可看出等式两边含义相同。
A − B = { x ∣ x ∈ A , x ∉ B } A-B=\{x|x\in A, x\notin B\} A−B={x∣x∈A,x∈/B}
X − B = { x ∣ x ∈ X , x ∉ B } X-B=\{x|x\in X, x\notin B\} X−B={x∣x∈X,x∈/B}
A ∩ ( X − B ) = { x ∣ x ∈ A , x ∈ ( X − B ) } = { x ∣ x ∈ A , x ∉ B } A\cap(X-B)=\{x | x\in A, x\in (X-B)\}=\{x | x\in A, x\notin B\} A∩(X−B)={x∣x∈A,x∈(X−B)}={x∣x∈A,x∈/B}
- 试证 X − ( B − A ) = ( X − B ) ∪ A , ∀ A , B ⊂ X X-(B-A)=(X-B)\cup A, \forall A,B\subset X X−(B−A)=(X−B)∪A,∀A,B⊂X.
根据德摩根律, X − ( B − A ) = X − ( B ∩ ( X − A ) ) = ( X − B ) ∪ ( X − ( X − A ) ) X-(B-A)=X-(B\cap(X-A))=(X-B)\cup(X-(X-A)) X−(B−A)=X−(B∩(X−A))=(X−B)∪(X−(X−A))
其中用差集定义列举即可得知 X − ( X − A ) = A X-(X-A)=A X−(X−A)=A
- 判断映射 f : R → R f:R\to R f:R→R是否是一一的(单射)、到上的(满射)。
f ( x ) = x 3 f(x)=x^3 f(x)=x3,双射
f ( x ) = x 2 f(x)=x^2 f(x)=x2,非单非满
f ( x ) = e x f(x)=e^x f(x)=ex,单射
f ( x ) = cos x f(x)=\cos x f(x)=cosx,非单非满
f ( x ) = 5 f(x)=5 f(x)=5,非单非满
- 判断下面说法正确与否
- 正切函数是由 R R R到 R R R的映射。否,定义域并非 R R R
- 对数函数是由 R R R到 R R R的映射。否,定义域并非 R R R
- ( a , b ] ⊂ R (a,b]\subset R (a,b]⊂R用通常拓扑衡量是开集。否,无法表示为开区间之并
- [ a , b ] ⊂ R [ a,b ]\subset R [a,b]⊂R用通常拓扑衡量是闭集。是,它的补集可以表示为无限个开区间之并。
- 举出一个反例证明命题“ ( R , T u ) (R,T_u) (R,Tu)的无限个开子集之交为开子集”是假命题。
( R , T u ) (R,T_u) (R,Tu)指的是 R R R上的通常拓扑,开子集定义为能表示为开区间之并的集合。
构造一系列开子集, ( − 1 1 , 1 1 ) , ( − 1 2 , 1 2 ) , ⋯ , ( − 1 n , 1 n ) (-\frac{1}{1},\frac{1}{1}), (-\frac{1}{2},\frac{1}{2}),\cdots ,(-\frac{1}{n},\frac{1}{n}) (−11,11),(−21,21),⋯,(−n1,n1),当 n n n是无穷时,这无限个开子集之交是一个闭集 [ 0 ] [0] [0]。
- 证明诱导拓扑定义满足拓扑的基本定义。
拓扑的基本定义有三个条件,逐个检验即可:
- 证明 A A A和 ∅ \varnothing ∅是开子集。
A A A一定是开子集,根据诱导拓扑的定义 T S = { V ⊂ A ∣ ∃ O ∈ T , V = A ∩ O } T_S=\{V\subset A | \exist O\in T, V=A\cap O\} TS={V⊂A∣∃O∈T,V=A∩O}
V V V取 A A A时,肯定存在 O = X O=X O=X(这是由拓扑 ( X , T ) (X,T) (X,T)基本性质决定的),使得 A = A ∩ X A=A\cap X A=A∩X
∅ \varnothing ∅同理- 证明有限交。
即证明 T S T_S TS中有限个元素之交仍然是 T S T_S TS的元素。
假设 V 1 , V 2 , ⋯ , V n ∈ T S V_1,V_2,\cdots , V_n\in T_S V1,V2,⋯,Vn∈TS,必然 ∃ O 1 , O 2 , ⋯ , O n ∈ T \exists O_1,O_2,\cdots , O_n\in T ∃O1,O2,⋯,On∈T,使得 V 1 = A ∩ O 1 , V 2 = A ∩ O 2 , ⋯ , V n = A ∩ O n V_1=A\cap O_1,V_2=A\cap O_2, \cdots , V_n=A\cap O_n V1=A∩O1,V2=A∩O2,⋯,Vn=A∩On,故 V 1 ∩ V 2 ∩ ⋯ ∩ V n = A ∩ ( O 1 ∩ O 2 ∩ ⋯ ∩ O n ) V_1\cap V_2\cap \cdots \cap V_n=A\cap (O_1 \cap O_2\cap \cdots \cap O_n) V1∩V2∩⋯∩Vn=A∩(O1∩O2∩⋯∩On),故对于有限交 V = V 1 ∩ V 2 ∩ ⋯ ∩ V n ⊂ A V=V_1\cap V_2\cap \cdots \cap V_n\subset A V=V1∩V2∩⋯∩Vn⊂A,总存在 O = O 1 ∩ O 2 ∩ ⋯ ∩ O n ∈ T O=O_1 \cap O_2 \cap \cdots \cap O_n\in T O=O1∩O2∩⋯∩On∈T,使得 V = A ∩ O V=A\cap O V=A∩O- 证明无限并。
假设有无限个 V α = A ∩ O α ⊂ A V_\alpha=A\cap O_\alpha\subset A Vα=A∩Oα⊂A,对于 V = ⋃ α V a = ⋃ α ( A ∩ O α ) = A ∩ ⋃ α O α = A ∩ O V=\underset{\alpha}\bigcup V_a=\underset{\alpha}\bigcup (A\cap O_\alpha)=A\cap\underset{\alpha}\bigcup O_\alpha=A\cap O V=α⋃Va=α⋃(A∩Oα)=A∩α⋃Oα=A∩O
- 举例证明 ( R 3 , T u ) (R^3, T_u) (R3,Tu)存在不开不闭的子集。
R R R上通常拓扑很容易找到一个不开不闭的子集,比如 [ 1 , 3 ) [1,3) [1,3),一边开一边闭。
R 3 R^3 R3是 R R R的乘积拓扑,而 [ 1 , 3 ) [1,3) [1,3)的笛卡尔积,形成一个半开半闭的立方体 [ 1 , 3 ) 3 [1,3)^3 [1,3)3,这就是一个不开不闭的子集。因为显然点 ( 1 , 1 , 1 ) ∈ R 3 (1,1,1)\in R^3 (1,1,1)∈R3不能由开球之并取到。
- 常值映射 f : ( X , T X ) → ( Y , T Y ) f:(X, T_X)\to (Y, T_Y) f:(X,TX)→(Y,TY)是否连续?说明原因。
设 y 0 ∈ Y y_0\in Y y0∈Y,且 f ( x ) = y 0 , ∀ x ∈ X f(x)=y_0,\forall x\in X f(x)=y0,∀x∈X,连续就意味着,对于任意包含 y 0 y_0 y0的开子集,其原像也是开子集。由映射关系可知,对任意包含 y 0 y_0 y0的集合,其原像都是 X ∈ T X X\in T_X X∈TX,故映射连续。
- 设 T D T_D TD是 X X X上的离散拓扑, T C T_C TC是 Y Y Y上的凝聚拓扑,找出从 ( X , T D ) (X,T_D) (X,TD)到 ( Y , T C ) (Y,T_C) (Y,TC)的所有连续映射,找出从 ( Y , T C ) (Y,T_C) (Y,TC)到 ( X , T D ) (X,T_D) (X,TD)的所有连续映射。
首先找从 ( X , T D ) (X,T_D) (X,TD)到 ( Y , T C ) (Y,T_C) (Y,TC)的连续映射,连续意味着,任何 T C T_C TC中的开子集,其逆像是 T D T_D TD中的开子集。由于 T C T_C TC中的开子集只有 Y Y Y和 ∅ \varnothing ∅, ∅ \varnothing ∅的逆像肯定仍然是 ∅ \varnothing ∅,因此只要要求 f − 1 [ Y ] ∈ T D f^{-1}[Y]\in T_D f−1[Y]∈TD即可。根据映射的基本定义, f − 1 [ Y ] = X ∈ T D f^{-1}[Y]=X\in T_D f−1[Y]=X∈TD,因此所有映射都是连续的。
然后找从 ( Y , T C ) (Y,T_C) (Y,TC)到 ( X , T D ) (X,T_D) (X,TD)的连续映射,即要求所有 X X X的子集,逆像都属于 { Y , ∅ } \{Y,\varnothing\} {Y,∅},那么只能是常值映射满足此要求。因为如果有两个不同的像,就 X X X就有两个不同的子集,都要求 Y Y Y是子集的逆像,但根据映射的定义,这是不可能的。
- 证明拓扑空间点连续的定义和映射连续的定义的等价性。
等价性意味着可以互相推导出,设映射为 f : ( X , T X ) → ( Y , T Y ) f:(X,T_X)\to(Y,T_Y) f:(X,TX)→(Y,TY)。
- 逐点连续 → \to →映射连续
∀ B ∈ T Y \forall B\in T_Y ∀B∈TY,总可以分为三类, ∅ \varnothing ∅,与值域有交集,与值域无交集。
其中,如果 B B B是 ∅ \varnothing ∅或与值域无交集,那么 f − 1 [ B ] = ∅ ∈ T X f^{-1}[B]=\varnothing\in T_X f−1[B]=∅∈TX;
如果 B B B与值域有交集,则可以取到像 y ∈ B y\in B y∈B,其逆像 x ∈ X x\in X x∈X,由于逐点连续,那么 x x x处也连续,那么必然存在 x ∈ A ∈ T X x\in A\in T_X x∈A∈TX,使得 f [ A ] = B f[A]=B f[A]=B;
即,对任意 B B B,逆像都是属于 T X T_X TX,所证成立。- 映射连续 → \to → 逐点连续
思路类似,同样挑出与值域有交集的 B ∈ T Y B\in T_Y B∈TY,其逆像 A A A必然属于 T X T_X TX;
对任意一点 x ∈ A ∈ T X x\in A\in T_X x∈A∈TX,找到其像 y y y和包含 y y y的 B B B,则必然存在 A ∈ T X A\in T_X A∈TX,使得 x ∈ A x\in A x∈A,且 f [ A ] = B f[A]=B f[A]=B,故 x x x点连续。
- 试证任意开区间 ( a , b ) ⊂ R (a,b)\subset R (a,b)⊂R与 R R R同胚。
同胚就意味着存在一个逆映射和本身都连续的双射, f : ( a , b ) → R f:(a,b)\to R f:(a,b)→R
很容易构造出这样的一个双射:
f ( x ) = tan ( π ( b − a ) ( x − a + b 2 ) ) , x ∈ ( a , b ) f(x)=\tan(\frac{\pi}{(b-a)}(x-\frac{a+b}{2})), x\in (a,b) f(x)=tan((b−a)π(x−2a+b)),x∈(a,b)
- 设 X 1 ⊂ R , X 2 ⊂ R X_1\subset R, X_2\subset R X1⊂R,X2⊂R,其中 X 1 = ( 1 , 2 ) ∪ ( 2 , 3 ) X_1=(1,2)\cup (2,3) X1=(1,2)∪(2,3), X 2 = ( 1 , 2 ) ∪ [ 2 , 3 ) X_2=(1,2)\cup [2,3) X2=(1,2)∪[2,3),设 T 1 T_1 T1和 T 2 T_2 T2分别是 ( R , T u ) (R,T_u) (R,Tu)在 X 1 X_1 X1和 X 2 X_2 X2上的诱导拓扑,拓扑空间 ( X 1 , T 1 ) (X_1,T_1) (X1,T1)和 ( X 2 , T 2 ) (X_2, T_2) (X2,T2)是否连通?
连通的定义是,除了 X X X和 ∅ \varnothing ∅外,没有即开又闭的子集。
( X 1 , T 1 ) (X_1,T_1) (X1,T1)显然不连通,集合 ( 1 , 2 ) ∈ T 1 (1,2)\in T_1 (1,2)∈T1就是一个即开又闭的子集;
( X 2 , T 2 ) (X_2,T_2) (X2,T2)是连通的
- 任意集合 X X X配以离散拓扑,所得的拓扑空间是否连通?
离散拓扑中,所有子集都是开子集,那么所有子集(补集)也都是闭子集,所有子集都既开又闭,必然不连通。
- 设 A ⊂ B A\subset B A⊂B,试证:(a) A ˉ ⊂ B ˉ \bar{A}\subset \bar{B} Aˉ⊂Bˉ,提示 A ⊂ B A\subset B A⊂B说明 B ˉ \bar{B} Bˉ是含 A A A的闭集;(b) i ( A ) ⊂ i ( B ) i(A)\subset i(B) i(A)⊂i(B)
先回顾一下概念: A A A的闭包 A ˉ \bar{A} Aˉ是所有包含 A A A的闭集的交集; A A A的内部 i ( A ) i(A) i(A)是所有 A A A包含的开集的并集。
(a). 根据提示可知, B ˉ \bar{B} Bˉ是包含 A A A的闭集,又由于 A ˉ \bar{A} Aˉ是所有包含 A A A的闭集的交集,所有 A ˉ = ⋂ α C α \bar{A}=\underset{\alpha}\bigcap C_\alpha Aˉ=α⋂Cα,其中,某个 C α = B ˉ C_\alpha=\bar{B} Cα=Bˉ,因此, A ˉ ⊂ B ˉ \bar{A}\subset \bar{B} Aˉ⊂Bˉ。
(b). 和上述思路一致, A A A包含的所有开集也必然被 B B B包含。
- 试证明 x ∈ A ˉ ↔ x x\in \bar{A}\leftrightarrow x x∈Aˉ↔x 的任一邻域与 A A A的交集非空。
回顾一下邻域的概念,邻域是一个集合,它能被视为邻域需要存在一个开子集被它包含,且此开子集有元素 x x x。
- 从左推右 ⟹ \implies ⟹
反证法,设开子集 O O O是 x x x的邻域,且 O ∩ A = ∅ O\cap A=\varnothing O∩A=∅,故 A ⊂ X − O A\subset X-O A⊂X−O,由上一题可知, A ˉ ⊂ X − O \bar{A}\subset X-O Aˉ⊂X−O,因为 X − O X-O X−O本身就是闭集。故 x ∈ X − O x\in X-O x∈X−O,矛盾。- 从右推左 ⟸ \impliedby ⟸
反证法,假设 x ∉ A ˉ x\notin \bar{A} x∈/Aˉ,且 ∀ O \forall O ∀O作为 x x x的开邻域, O ∩ A ≠ ∅ O\cap A\neq \varnothing O∩A=∅。总存在闭集 B B B,使得 A ⊂ B A\subset B A⊂B且 x ∉ B x\notin B x∈/B,故 x ∈ X − B x\in X-B x∈X−B,那么 ( X − B ) ∩ A = ∅ (X-B)\cap A=\varnothing (X−B)∩A=∅且 ( X − B ) (X-B) (X−B)是开邻域,与前设矛盾。
- 试证明 R R R不是紧致的。
回顾紧致的定义,任一开覆盖都有有限开覆盖,则紧致。
很明显 R R R不是紧致的,可以找到一系列开子集 ( − n , − n + 2 ) , ( − n + 1 , − n + 3 ) ⋯ ( − 2 , 0 ) , ( 1 , 3 ) , ⋯ , ( n , n + 2 ) (-n,-n+2),(-n+1,-n+3) \cdots (-2,0),(1,3), \cdots, (n,n+2) (−n,−n+2),(−n+1,−n+3)⋯(−2,0),(1,3),⋯,(n,n+2), n n n为无穷大。这一系列开子集可以覆盖 R R R,但有限的子集不能覆盖 R R R,所以不是紧致的。