Z 字形变换原题地址
方法一:利用二维矩阵模拟
对于特殊情况,Z 字形变换后只有一行或只有一列,则变换后的字符串和原字符串相同。
对于一般情况,我们可以考虑按照题目要求,把字符串按照 Z 字形存储到二维数组中,再横向遍历所有有效字符。
假设 Z 字形变换后的矩阵有 r 行,原字符串的长度为 n 。
Z 字形变换是按照周期 t 先向下,再向右上运动。一个周期 t=r+(r-2)=r*2-2 。
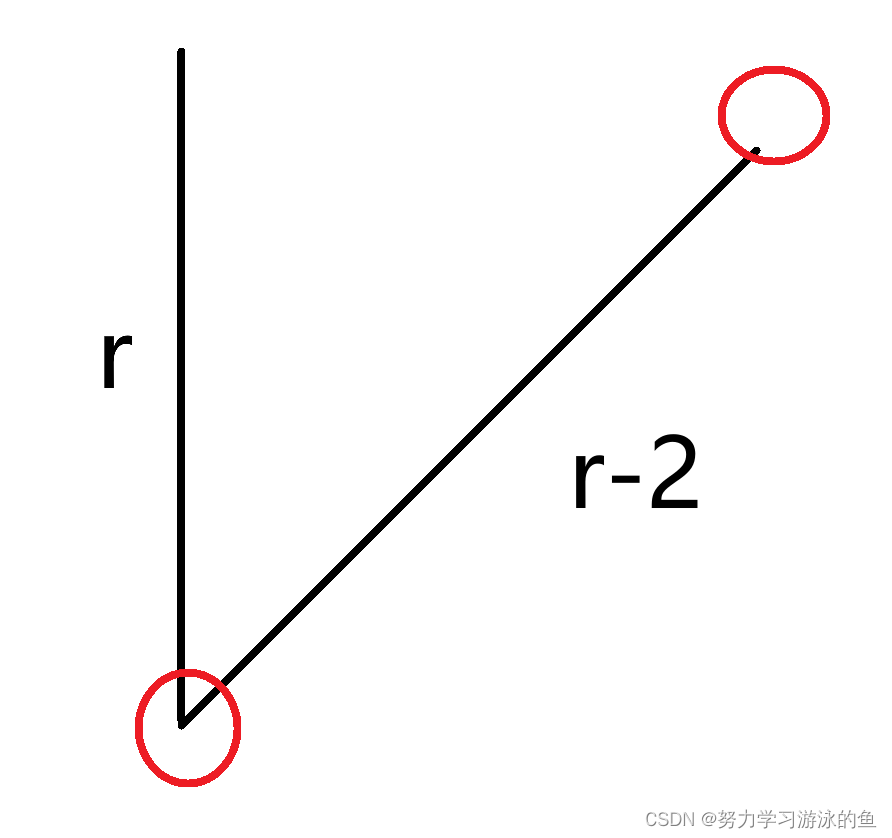
其中 r-2 不包含两个红圈的位置。 一个周期 t 内的行数为 r 行,列数为 1+(r-2)=r-1 列,即最左边的一列以及中间的 r-2 列。矩阵的周期数为 ,即 (n+t-1)/t ,加上的 t-1 是为了向上取整。矩阵的总列数为 周期数 * 每个周期的列数,即 c=(n+t-1)/t*(r-1) 。
那么,什么时候向下走,什么时候向右上方走呢?这要看当前处在周期的什么位置。假设当前遍历到下标为 i 的字符,如果 imodt<r-1 ,即当前处在周期的前 r-1 个位置,就需要向下走,否则就要向右上方走。
// 方法一:利用二维矩阵模拟
class Solution
{
public:string convert(string s, int numRows){int n = s.size();int r = numRows; // 行数// 只有一行或者只有一列if (r == 1 || r >= n){return s;}// 周期 t=r+r-2int t = r * 2 - 2;// 一共有 (n/t) 向上取整 个周期// 即 (n+t-1)/t 个周期// 每个周期有 1+r-2=r-1 列int c = (n + t - 1) / t * (r - 1); // 列数// 构造矩阵,即 r 个 string 的数组,每个 string 的长度为 cvector<string> mat(r, string(c, 0));int x = 0, y = 0; // 左上角for (int i = 0; i < n; ++i){mat[x][y] = s[i];// 周期前 r-1 次都是向下移动// 否则向右上方移动if (i % t < r - 1){++x;}else{--x;++y;}}string ans;// 拼接每行有效字符for (auto& row : mat){for (auto ch : row){if (ch){ans += ch;}}}return ans;}
};方法二:压缩矩阵空间
模拟时,可以不按照 Z 字形存储到矩阵中,而是根据当前字符在第几行,就存储在该行的最后一个位置,即尾插到当前行。这样的话可以节省矩阵的空间。
如果采用这种方案,就只需要考虑是向下走还是向上走。按照相同的思路,当 imodt<r-1 ,即当前周期的前 r-1 个字符,需要向下走,反之就向上走。
// 方法二:压缩矩阵空间
class Solution
{
public:string convert(string s, int numRows){int n = s.size();int r = numRows; // 行数// 只有一行或只有一列if (r == 1 || r >= n){return s;}vector<string> mat(r);// 周期 t=r+r-2int t = r * 2 - 2;int x = 0; // 在第几个 string 后面添加字符for (int i = 0; i < n; ++i){mat[x] += s[i];// 每个周期前 r-1 次向下移动if (i % t < r - 1){++x;}else{--x;}}string ans;// 拼接所有行for (auto& row : mat){ans += row;}return ans;}
};方法三:方法二的另一种写法
在考虑是向下走还是向上走时,可以不用计算在当前周期的第几个位置,而是直接判断当前所处位置是否在最上面还是最下面。也就是说,如果当前在第 x 行,若 x==1 或者 x==r-1 ,说明要转向,本来是向下走就要转为向上走,本来是向上走就要转为向下走。
我们可以定义一个 flag ,如果 flag=1 代表向下走, flag=-1 代表向上走,每次只需要 x+=flag 就能求出新的所在行 x 了。如果要转向,只需执行 flag=-flag 。
// 方法三:方法二的另一种写法,利用 flag 记录何时转向
class Solution
{
public:string convert(string s, int numRows){int n = s.size();int r = numRows; // 行数// 只有一行或只有一列if (r == 1 || r >= n){return s;}vector<string> mat(r);int x = 0; // 在第几个 string 后面添加字符int flag = 1; // 行转向标志, 1 代表向下走, -1 代表向上走for (int i = 0; i < n; ++i){mat[x] += s[i];x += flag;// 转向if (x == r - 1 || x == 0){flag = -flag;}}string ans;// 拼接所有行for (auto& row : mat){ans += row;}return ans;}
};方法四:直接构造
前三种方法都需要构造一个新的矩阵来模拟,我们可以考虑直接构造,也就是直接取出原字符串的字符来构造 ans 字符串。这就需要找出 Z 字形变换的规律,看图:

按照“Z字形”的顺序来看,就是 0->1->2->3->...->t-2->t-1->t->t+1->t+2->...->2t-2->2t-1->2t->2t+1->2t+2->...
如果我们横着看呢? 我们用i来控制行, i 从 0 递增到 r-1 。再用 j 控制列, j 从 0 开始,每次递增 t ,也就是 0,t,2t,3t,... 。那么下图中,每个周期都是线 + 方框,线是 i+j ,框柱的是 j+t-i 。

对于每一行,都有线,但是第 0 行和第 r-1 行没有方框内的元素,利用这点直接构造字符串即可。
// 方法四:直接构造
class Solution
{
public:string convert(string s, int numRows){int n = s.size();int r = numRows; // 行数// 只有一行或只有一列if (r == 1 || r >= n){return s;}string ans;// 周期 t=r+r-2int t = r * 2 - 2;for (int i = 0; i < r; ++i){for (int j = 0; j + i < n; j += t){// 当前周期第一个字符ans += s[j + i];// 若不是第一行和最后一行,还有第二个字符if (0 < i && i < r - 1 && j + t - i < n){ans += s[j + t - i];}}}return ans;}
};