123.买卖股票的最佳时机III

题目链接：123.买卖股票的最佳时机III
文章讲解：代码随想录|123.买卖股票的最佳时机III
视频讲解：123.买卖股票的最佳时机III

思路

1.本题最多可以完成两笔交易，那么一共有五个状态：
dp[i][0]:不持有
dp[i][1]:第一次持有(已经买了或今天购买第一次股票)
dp[i][2]:第一次不持有(已经卖了或今天卖掉第一次股票)
dp[i][3]:第二次持有
dp[i][4]:第二次不持有
2.状态转移
dp[i][0] = dp[i-1][0]
dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i])
dp[i][2] = max(dp[i-1][2], dp[i-1][1] + prices[i])
dp[i][3] = max(dp[i-1][3], dp[i-1][2] - prices[i])
dp[i][4] = max(dp[i-1][4], dp[i-1][3] + prices[i])
3.初始化
dp[0][0] = 0;
dp[0][1] = - prices[0]
dp[0][2] = - prices[0] 相当于第0天第一次买入了，第一次卖出了，然后再买入一次（第二次买入），那么现在手头上没有现金，只要买入，现金就做相应的减
dp[0][3] = 0
4.从前向后遍历
5.
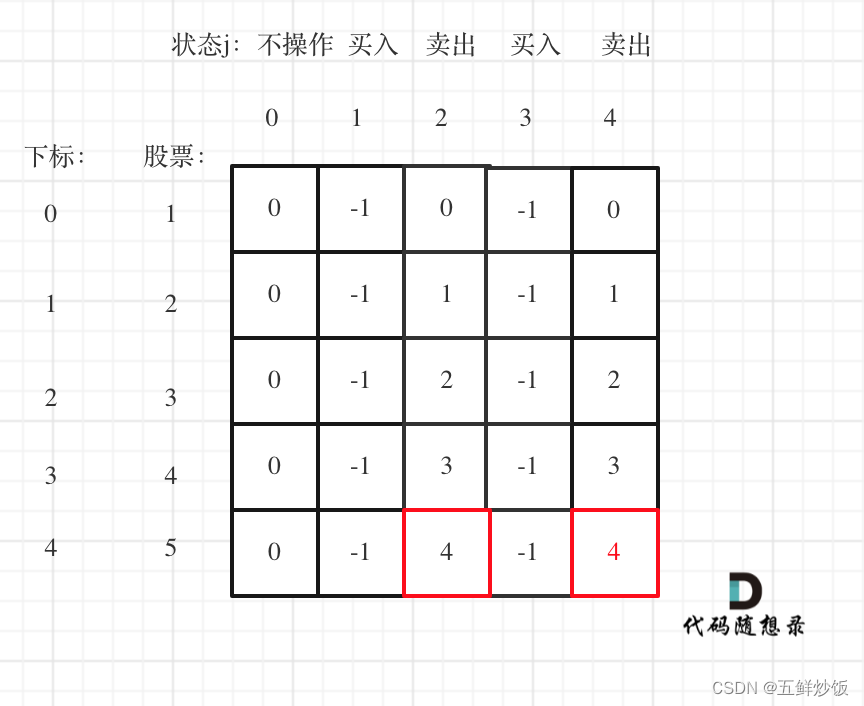
现在最大的时候一定是卖出的状态，而两次卖出的状态现金最大一定是最后一次卖出。如果想不明白的录友也可以这么理解：如果第一次卖出已经是最大值了，那么我们可以在当天立刻买入再立刻卖出。所以dp[4][4]已经包含了dp[4][2]的情况。也就是说第二次卖出手里所剩的钱一定是最多的。

代码

class Solution {
public:int maxProfit(vector<int>& prices) {if (prices.size() == 0) return 0;vector<vector<int>> dp(prices.size(), vector<int>(5, 0));dp[0][1] = -prices[0];dp[0][3] = -prices[0];for (int i = 1; i < prices.size(); i++) {dp[i][0] = dp[i - 1][0];dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i]);dp[i][2] = max(dp[i - 1][2], dp[i - 1][1] + prices[i]);dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - prices[i]);dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i]);}return dp[prices.size() - 1][4];}
};

188.买卖股票的最佳时机IV

题目链接：188.买卖股票的最佳时机IV
文章讲解：代码随想录|188.买卖股票的最佳时机IV

思路

最多可以完成k笔交易，思路跟上题一样

达到dp[i][1]状态，有两个具体操作：

操作一：第i天买入股票了，那么dp[i][1] = dp[i - 1][0] - prices[i]
操作二：第i天没有操作，而是沿用前一天买入的状态，即：dp[i][1] = dp[i - 1][1]
选最大的，所以 dp[i][1] = max(dp[i - 1][0] - prices[i], dp[i - 1][1]);

同理dp[i][2]也有两个操作：

操作一：第i天卖出股票了，那么dp[i][2] = dp[i - 1][1] + prices[i]
操作二：第i天没有操作，沿用前一天卖出股票的状态，即：dp[i][2] = dp[i - 1][2]
所以dp[i][2] = max(dp[i - 1][1] + prices[i], dp[i - 1][2])

然后类比剩下的状态：

for (int j = 0; j < 2 * k - 1; j += 2) {dp[i][j + 1] = max(dp[i - 1][j + 1], dp[i - 1][j] - prices[i]);dp[i][j + 2] = max(dp[i - 1][j + 2], dp[i - 1][j + 1] + prices[i]);
}

代码

class Solution {
public:int maxProfit(int k, vector<int>& prices) {if (prices.size() == 0) return 0;vector<vector<int>> dp(prices.size(), vector<int>(2 * k + 1, 0));for (int j = 1; j < 2 * k; j += 2) {dp[0][j] = -prices[0];}for (int i = 1;i < prices.size(); i++) {for (int j = 0; j < 2 * k - 1; j += 2) {dp[i][j + 1] = max(dp[i - 1][j + 1], dp[i - 1][j] - prices[i]);dp[i][j + 2] = max(dp[i - 1][j + 2], dp[i - 1][j + 1] + prices[i]);}}return dp[prices.size() - 1][2 * k];}
};