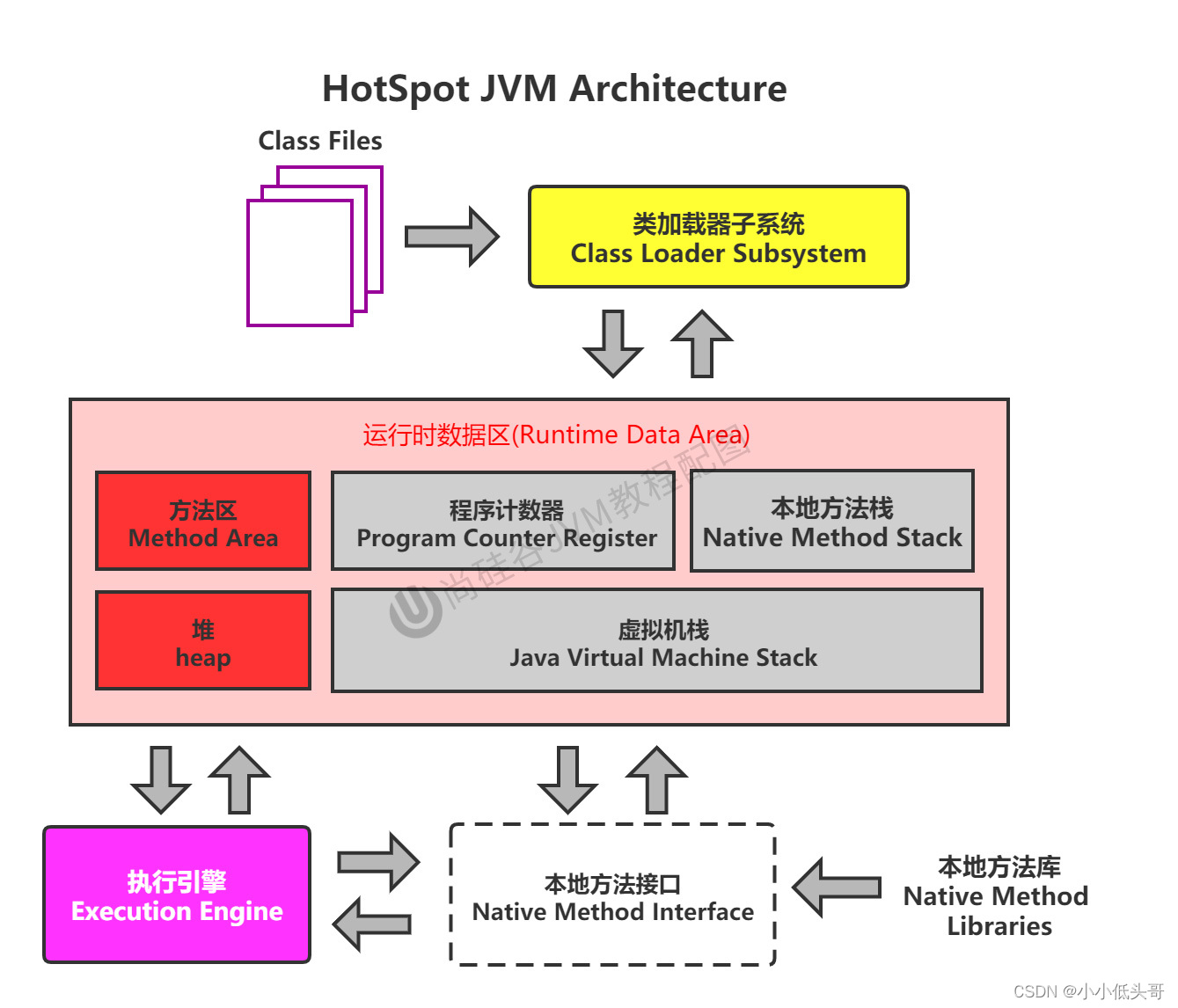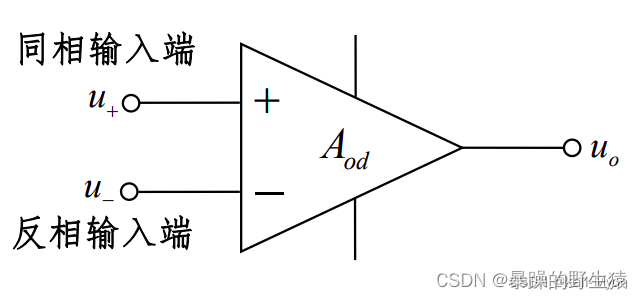
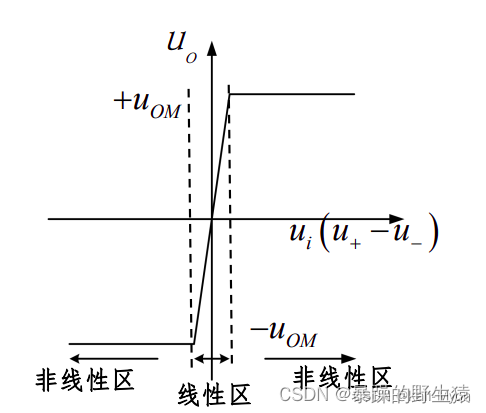
上图中，线性区的这条斜线的斜率，就是开环增益（或者叫开环放大倍数），对于理想运放，其开环增益为正无穷，当然对于市面上的运放产品，斜率是不可能无穷大的，一般为几万~几百万。

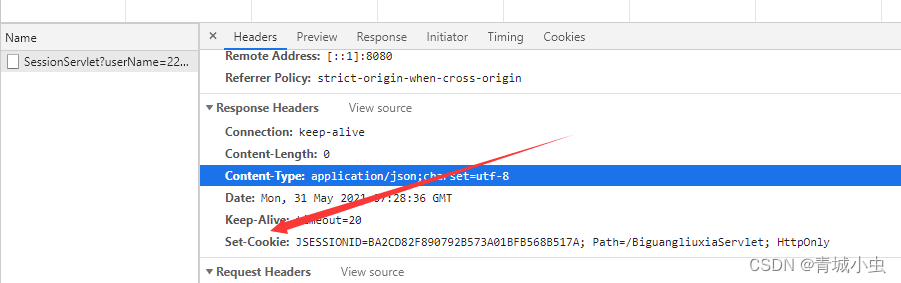
以TI的高速运放芯片OPA365为例，查询厂家给出的数据手册可见：

其开环增益Aol在负载为10k欧时为120分贝，根据分贝与倍数的转换公式：dB=20*lg(out/in)，可知其放大倍数Aol=out/in=10的6次方=100万倍

OPA365这款芯片的供电电压一般为5v，那么当差分输入电压为0.000005V时，运放的输出就会达到饱和，也即0.000005V*100万倍=5V。可以看到，只要有一丁点儿输入，哪怕是mV甚至uV输入，都可以导致运放输出饱和，所以运放一般不会单独使用，而是配合反馈电路：

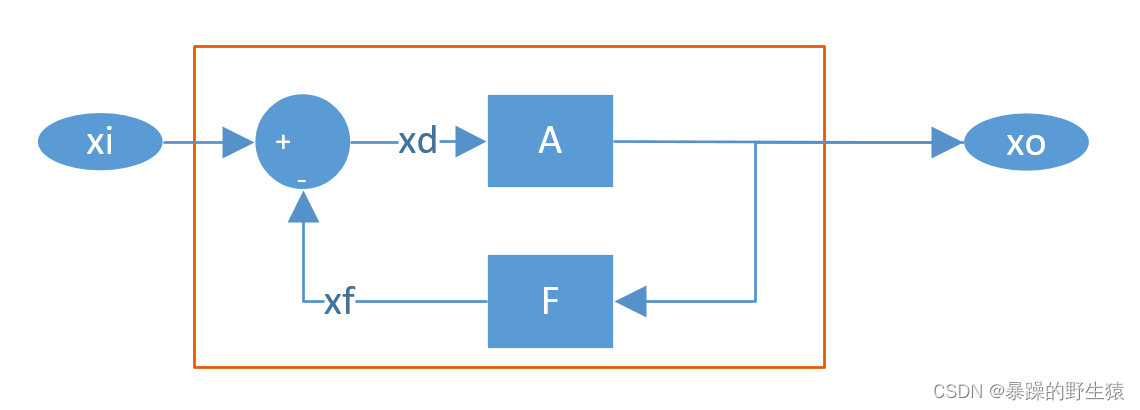
上图中，A为运放的开环放大增益，F为反馈电路的增益，那么红框部分（也即这个反馈系统）的闭环增益Af=A  /（1+AF）。仍然以OPA365为例，上图中xd只要达到了0.000005V，运放的输出就会饱和，也即xo就会=5V

假如有这样一个需求：制作一个电压放大器，放大倍数为2倍。也即当xi输入0v时，xo需要输出0v；当xi输入1v时，xo需要输出2v；当xi输入2.5v时，xo需要输出5v；

只需要令F=0.5,即可实现以上需求，当F=0.5时，闭环放大倍数Af=A  /（1+AF）=1000000 /（1+1000000*0.5）=1.999996倍≈2倍。也即当A远大于1时，Af≈1/F，这种情况被称为“深度负反馈”。深度负反馈的系统中，会呈现出一种有趣的特性：反馈量xf总是约等于输入量xi的。为什么会出现这种特性呢？下面计算一下：

在以上框图中：xd=xi-xf    --->  xo = xd*A     ----->   xf=xo*F

xf=xo*F=（xd*A）*F=xd*A*F=（xi-xf）*A*F

移项合并同类项得到：

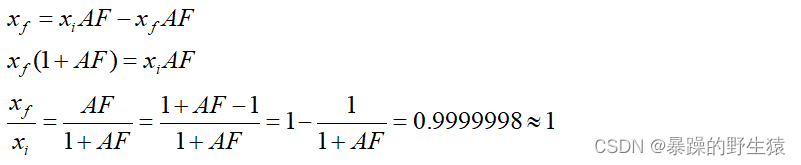
至此，我们知道了，xf 和 xi确实总是近似相等的。

而运放的输入信号xd=xi-xf，详细计算得到：

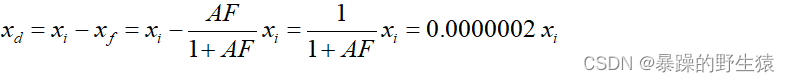
可见，只要xi输入<2.5v，xd就会<0.0000005V，也即运放就会工作在线性区，而不会饱和。

由于运放的输入xd为

可以认为u+和u-几乎相等，这就是“虚短”这个词的由来，就好像u+和u-端子被短路了一样，两者电压相等。

“虚断”这个词比较好解释，由于运放的输入阻抗极高（u+和u-的输入阻抗都很高），市面上的运放产品一般为百万Ω以上级别，因此，从u+和u-端子流入运放内部的电流，一般为uA或者nA级别，约等于没有，就好像断路了一样。

下图来自百度词条“深度负反馈”

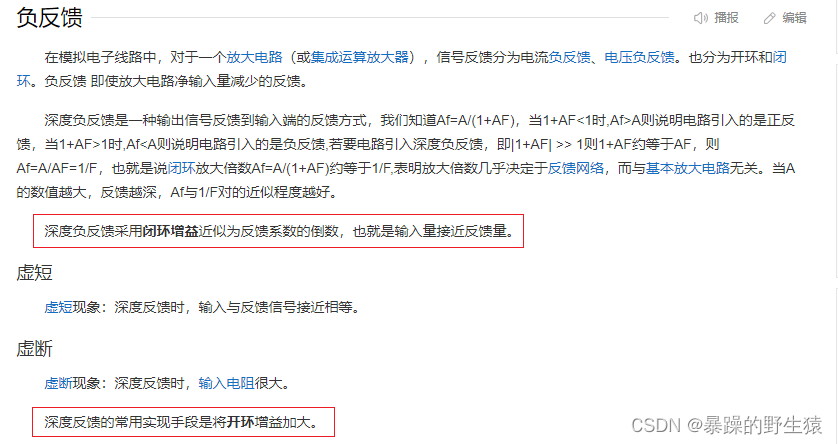
参考：

集成运算放大器的线性应用（模电速成）_模电中线性区的有哪些-CSDN博客