1、两数之和
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。
你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。
你可以按任意顺序返回答案。
示例 1:
输入:nums = [2,7,11,15], target = 9
输出:[0,1]
解释:因为 nums[0] + nums[1] == 9 ,返回 [0, 1] 。
示例 2:
输入:nums = [3,2,4], target = 6
输出:[1,2]
示例 3:
输入:nums = [3,3], target = 6
输出:[0,1]
提示:
2 <= nums.length <= 104-109 <= nums[i] <= 109-109 <= target <= 109- 只会存在一个有效答案
思路解答:
方法1、二层for循环 暴力解决
方法2、采用字典存储加遍历 python中的字典底层为哈希表
def twoSum(self, nums: list[int], target: int) -> list[int]:hashtable = dict()for i, num in enumerate(nums):if target - num in hashtable:return [hashtable[target - num], i]else:hashtable[num] = ireturn []
2、字母异位词分组
给你一个字符串数组,请你将 字母异位词 组合在一起。可以按任意顺序返回结果列表。
字母异位词 是由重新排列源单词的所有字母得到的一个新单词。
示例 1:
输入: strs = ["eat", "tea", "tan", "ate", "nat", "bat"]
输出: [["bat"],["nat","tan"],["ate","eat","tea"]]
示例 2:
输入: strs = [""]
输出: [[""]]
示例 3:
输入: strs = ["a"]
输出: [["a"]]
提示:
1 <= strs.length <= 1040 <= strs[i].length <= 100strs[i]仅包含小写字母
思路解答:
互为字母异位词的两个字符串包含的字母相同,且相同字母的个数也相同。 直接排序即可。
def groupAnagrams(self, strs: list[str]) -> list[list[str]]:result = collections.defaultdict(list)for s in strs:key = ''.join(sorted(s))result[key].append(s)return list(result.values())
3、最长连续序列
给定一个未排序的整数数组 nums ,找出数字连续的最长序列(不要求序列元素在原数组中连续)的长度。
请你设计并实现时间复杂度为 O(n) 的算法解决此问题。
示例 1:
输入:nums = [100,4,200,1,3,2]
输出:4
解释:最长数字连续序列是 [1, 2, 3, 4]。它的长度为 4。
示例 2:
输入:nums = [0,3,7,2,5,8,4,6,0,1]
输出:9
提示:
0 <= nums.length <= 105-109 <= nums[i] <= 109
思路解答:
- 对于每个元素
num,检查num-1是否在哈希表(set集合基于哈希表实现)中,如果不存在,则num是一个连续序列的起点。 - 对于每个起点
start,依次增加start+1、start+2、start+3… 直到找不到下一个连续数字为止,记录当前连续序列的长度。 - 更新最长连续序列的长度。
def longestConsecutive(self, nums: list[int]) -> int:#去重 第一次不去重直接超时了- -num_set = set(nums)max_length = 0for num in num_set:if num - 1 not in num_set:current_num = numcurrent_length = 1while current_num + 1 in num_set:current_num += 1current_length += 1max_length = max(max_length, current_length)return max_length
4、移动零
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
请注意 ,必须在不复制数组的情况下原地对数组进行操作。
示例 1:
输入: nums = [0,1,0,3,12]
输出: [1,3,12,0,0]
示例 2:
输入: nums = [0]
输出: [0]
提示:
1 <= nums.length <= 104-231 <= nums[i] <= 231 - 1
思路解答:
直接遍历数组不为0的部分进行重新覆盖,剩余部分补0
def moveZeroes(self, nums: list[int]) -> None:i = 0for num in nums:if num != 0:nums[i] = numi += 1for j in range(i, len(nums)):nums[j] = 0
5、盛最多水的容器
给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
**说明:**你不能倾斜容器。
示例 1:
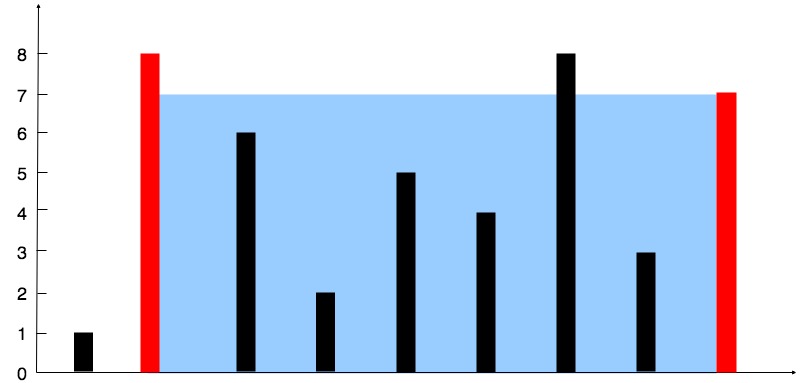
输入:[1,8,6,2,5,4,8,3,7]
输出:49
解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
示例 2:
输入:height = [1,1]
输出:1
提示:
n == height.length2 <= n <= 1050 <= height[i] <= 104
思路解答:
-
使用两个指针,一个指向数组的起始位置,另一个指向数组的结束位置。
-
计算两个指针所形成的容器的容量,即两个指针之间的距离乘以较小高度的值。
-
比较当前容量与之前的最大容量,更新最大容量。
-
移动较小高度的指针,重复步骤2和3,直到两个指针相遇。
def maxArea(self, height: list[int]) -> int:max_area = 0left = 0right = len(height) - 1while left < right:current_area = min(height[left], height[right]) * (right - left)max_area = max(max_area, current_area)if height[left] < height[right]:left += 1else:right -= 1return max_area
6、三数之和
给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ,同时还满足 nums[i] + nums[j] + nums[k] == 0 。请
你返回所有和为 0 且不重复的三元组。
**注意:**答案中不可以包含重复的三元组。
示例 1:
输入:nums = [-1,0,1,2,-1,-4]
输出:[[-1,-1,2],[-1,0,1]]
解释:
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。
注意,输出的顺序和三元组的顺序并不重要。
示例 2:
输入:nums = [0,1,1]
输出:[]
解释:唯一可能的三元组和不为 0 。
示例 3:
输入:nums = [0,0,0]
输出:[[0,0,0]]
解释:唯一可能的三元组和为 0 。
提示:
3 <= nums.length <= 3000-105 <= nums[i] <= 105
思路解答:
- 对数组进行排序。
- 遍历排序后的数组,对于每个固定的元素 nums[i],使用双指针 left 和 right 分别指向 i 的下一个元素和数组末尾。
- 在循环中,计算当前三个元素的和 sum = nums[i] + nums[left] + nums[right],如果 sum == 0,则找到一个满足条件的三元组,将其加入结果集。
- 如果 sum < 0,则将 left 右移一位;如果 sum > 0,则将 right 左移一位。
- 在移动指针时,需跳过重复的元素,以避免重复的三元组。
def threeSum(self, nums: list[int]) -> list[list[int]]:nums.sort()result = []for i in range(len(nums) - 2):#跳过重复元素if i > 0 and nums[i] == nums[i - 1]:continueleft, right = i + 1, len(nums) - 1while left < right:total = nums[i] + nums[left] + nums[right]if total == 0:result.append([nums[i], nums[left], nums[right]])while left < right and nums[left] == nums[left + 1]:left += 1while left < right and nums[right] == nums[right - 1]:right -= 1left += 1right -= 1elif total < 0:left += 1else:right -= 1return result


![xff注入 [CISCN2019 华东南赛区]Web111](https://img-blog.csdnimg.cn/direct/e9c14f1e4cf1451482822a9936fda0e4.png)