参考资料:用python动手学统计学
1、导入库
# 导入库
# 导入数据处理的库
import numpy as np
import pandas as pd
import scipy as sp
from scipy import stats
# 导入绘图的库
from matplotlib import pyplot as plt
import seaborn as sns
sns.set()
# 导入估计统计模型的库
import statsmodels.formula.api as smf
import statsmodels.api as sm2、数据准备
data=pd.DataFrame({'beer':np.array([45.3, 59.3, 40.4, 38. , 37. , 40.9, 60.2, 63.3, 51.1, 44.9, 47. ,53.2, 43.5, 53.2, 37.4, 59.9, 41.5, 75.1, 55.6, 57.2, 46.5, 35.8,51.9, 38.2, 66. , 55.3, 55.3, 43.3, 70.5, 38.8]),'temp':np.array([20.5, 25. , 10. , 26.9, 15.8, 4.2, 13.5, 26. , 23.3, 8.5, 26.2,19.1, 24.3, 23.3, 8.4, 23.5, 13.9, 35.5, 27.2, 20.5, 10.2, 20.5,21.6, 7.9, 42.2, 23.9, 36.9, 8.9, 36.4, 6.4])
})
data.head()
3、线性模型拟合
# 利用普通最小二乘法(ordinary least squares)拟合线性模型
lm=smf.ols(formula="beer~temp",data=data).fit()
# 查看模型的系数
lm.params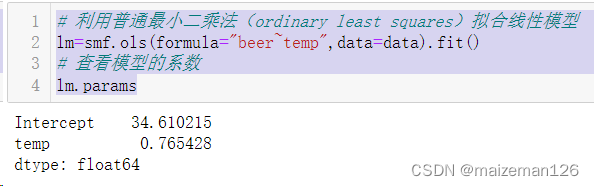
4、预测
当模型拟合完成后,可以用predict函数进行预测。当参数为空时,输出的是训练集对应的拟合值,如下:

在预测时可以指定气温的值,参数为dataframe格式。估计temp为0时的beer值,如下:
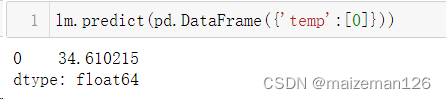
也可以用模型估计的系数来直接计算出对应的期望值,如下:
# 用线性模型的系数计算当temp为0时beer的期望值
beta0=lm.params[0]
beta1=lm.params[1]
temp=0
beta0+beta1*temp
5、模型评估——残差
原则上,我们应该在预测之前评估模型。模型的评估以分析残差为主。正态线性模型的残差应该服从均值为0的正态分布,所以我们要检查残差是否满足这个条件。
# 获取残差
resid=lm.resid
resid.head(3)
下面我们按照残差的计算公式获取残差,残差的计算公式为:
其中,y为实际值,为估计值(拟合值)。
计算过程如下:
# 计算估计值
y_hat=beta0+beta1*data.temp
# 计算残差
res=data.beer-y_hat
res.head(3)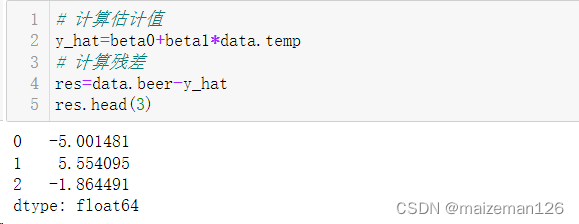
6、模型评估——决定系数
在summary函数的输出中,R-squared叫作决定系数。决定系数用来评估模型与已知数据的契合度。决定系数的计算式如下:
其中,y为相应变量的实际值,是模型的估计值(预测值),μ是y的均值。
如果相应变量的估计值(预测值)和实际值相等,则=1。
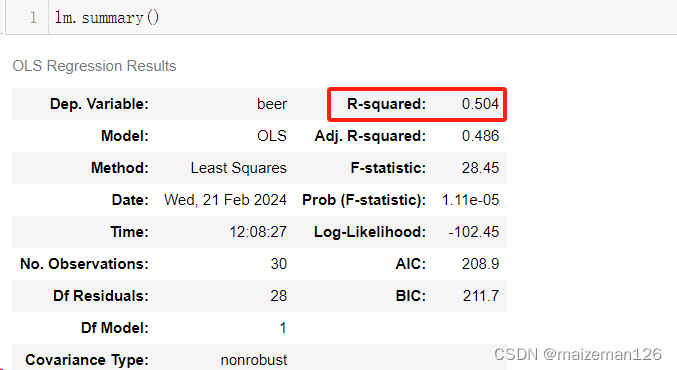
决定系数的获取方式如下:
# 方法一:直接获取
lm.rsquared
print("lm.rsquared: ",lm.rsquared)
# 方法二:按公式进行计算
mu=np.mean(data.beer)
y=data.beer
y_hat=lm.predict()
R_squared=np.sum((y_hat-mu)**2)/np.sum((y-mu)**2)
print("R_squared: ",R_squared)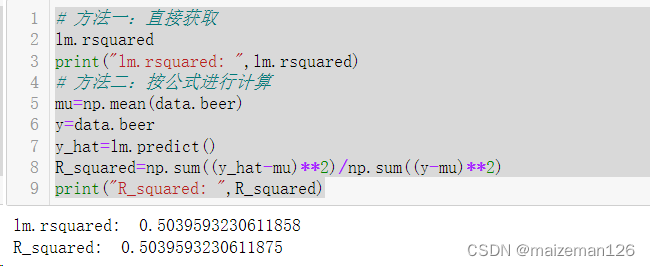
下面介绍决定系数的具体含义:由残差的计算公式变形可得
。决定系数的计算公式的分母可分解为下式:
相应变量的差异等于模型可预测的差异加上模型不可预测的残差平方和。因此,模型可以预测的差异在整体中所占的比例就是决定系数。决定系数的表达式也可以表示为:
当解释变量越多,决定系数越大。决定系数过大会导致过拟合,因此需要对决定系数进行修正(修正决定系数考虑了解释变量过多地惩罚制表,通过自由度修正了决定系数。)修正决定系数的数学公式如下:
其中,s为解释变量的个数。
修正决定系数的获取方式如下:
# 方法一:直接获取
lm.rsquared_adj
print("lm.rsquared_adj: ",lm.rsquared_adj)
# 方法二:按公式进行计算
n=len(data.beer)
s=1
mu=np.mean(data.beer)
y=data.beer
R_squared_adj=1-(np.sum(lm.resid**2)/(n-s-1))/(np.sum((y-mu)**2)/(n-1))
print("R_squared_adj: ",R_squared_adj)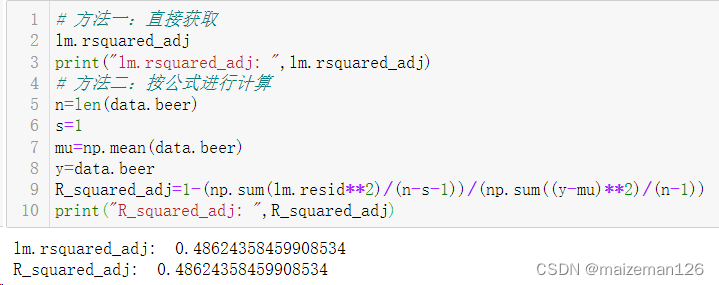
7、模型评估——残差的直方图和散点图
要观察残差的特征,最简单的方法就是绘制出它的直方图。
根据残差的直方图,我们可知残差大致左右对称,形状接近正态分布。
sns.histplot(lm.resid,kde=True)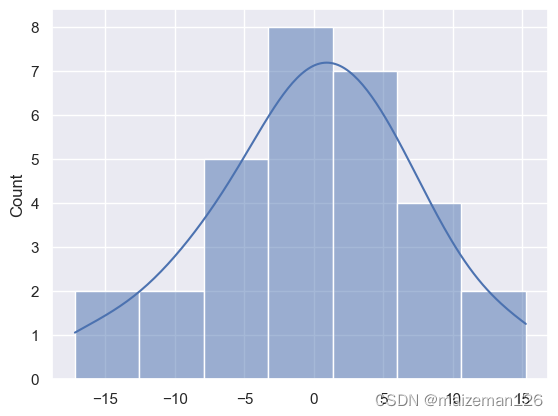
下面绘制横轴为拟合值、纵轴为残差的散点图,该图看起来是随机的,个数据都不相关也没有出现极端值。
sns.jointplot(x=lm.fittedvalues,y=lm.resid)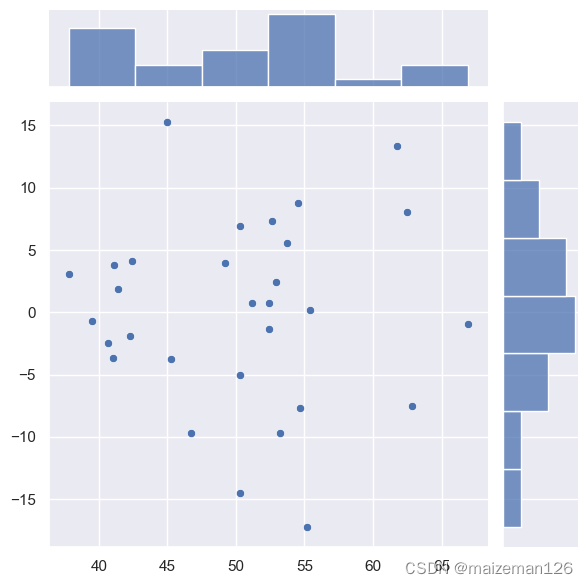
8、模型评估——残差的分位图
分位图是用来比较理论分位数(theoretical quantiles)与实际分位数(sample quantiles)的散点图,也叫Q-Q图。正态分布的百分位数就是理论分位数,通过图形对比理论分位数与真实数据的分位数,可以直观地判断残差是否服从正态分布分布。具体原理可以参考excel统计分析——Q-Q图_excel 画q-q图-CSDN博客
由下图可以看出,残差基本服从正态分布分布。
# 绘制Q-Q图,line=‘s’表示绘制正态分布标准线。
# 如果散点落在线上表示数据服从正态分布。
sm.qqplot(lm.resid,line='s')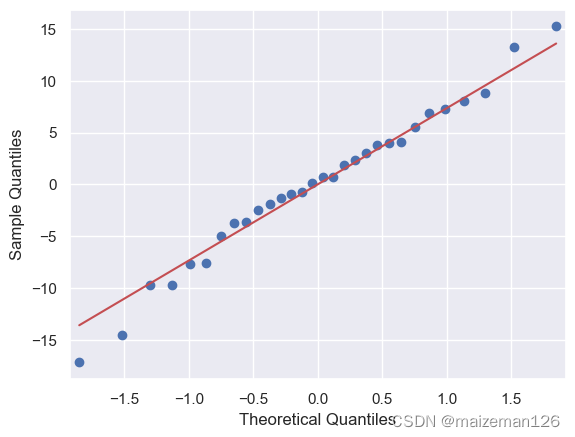
9、模型评估——根据summary函数的输出分析残差
利用summary函数查看其输出的第三个表:
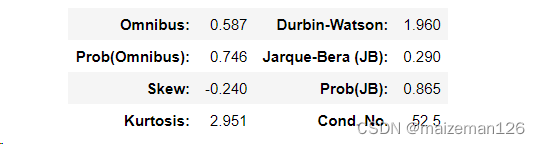
Prob(Omnibus) 和 Prob(JB) 是残差的正态性检验结果。p值大于0.05,并不代表残差确实不服从正态分布,此处的检验只能用来判断结果是否存在明显的问题。
要判断残差是否服从正态分布,还要观察skew(偏度)和kurtosis(峰度)的值。有此表可以skew=-0.240,接近0;kurtosis=2.951,接近3,基本服从正态分布分布。具体原理可参考:excel统计分析——偏度、峰度_excel的峰度是减3后的值吗-CSDN博客
Durbin-Watson表示残差的自相关程度,如果它的值在2附近,就说明没什么问题。在分析时间序列的数据时必须判断它是否在2附近。如果残差自相关,系数的检验结果便不可信,这个现象叫作伪回归。如果DurbinWatson统计量远大于2,就需要使用广义最小二乘法进一步讨论了。