【PyTorch][chapter 16][李宏毅深度学习][Neighbor Embedding][t-SNE]

前言：

前面LLE 讲了两个点在高维空间距离相近，通过降维后也要保持这种关系

但是如果两个点在高维空间距离很远（不属于K邻近）,降维后有可能叠加在一起了.

t-SNE(t-Distributed Stochastic Neighbor Embedding)是一种降维技术，LLE在进行降维时，都强调了降维后的相似的数据要尽可能地保持相似，但并没有说对于那些不相似的数据，要有多不相似这个问题.

这就导致了在进行降维时，可能导致数据的重叠问题，导致在低维空间中一样很难进行区分。

这时就需要另一种降维的方法——T-SNE。

高维重构
SNE
t-SNE
Python 代码

一高维重构

假设高维空间有m个点

$[x_1,x_2,...x_m]$

对于高维空间的两个点 $x_i,x_j$

$p_{j|i}=\frac{exp(-||x_i-x_j||^2)}{\sum_{k\neq i}exp(||x_i-x_k||^2)}$

$p_{j|i}$ 代表 $x_j$ 是 $x_i$ 的“邻居”的概率,值越大，说明两者越“临近”；

$\sigma_i$ 是 $x_i$ 最临近的N个点的方差值,其中N是一个超参数.

二 SNE

2.1 低维重构

假设低维空间的两个点 $a_i,a_j$ ,对应高维空间的两个点 $x_i,x_j$

$a_i,a_j$ 之间也符合上面分布

$q_{j|i}=\frac{exp(-||a_i-a_j||^2)}{\sum_{k \neq i}exp(-||a_i-a_k||^2)}$

设 $z_{j} =-||a_i-a_j||^2$

则 $q_{ji}=\frac{exp(z_{j})}{\sum_{k=1}^{K}exp(z_k)}$

该模型中：求解的是 $a_i,a_j$

2.2 损失函数

如何得到 $a_i,a_j$ ,使用KL 散度,使得高维空间和低维空间的样本概率分布一致

$J=\sum_i\sum_j p_{j|i}log \frac{p_{j|i}}{q_{j|i}}$

求 $a_i,a_j$ 的微分可以简化为

$J=-\sum_i\sum_j p_{ji}log q_{ji}$

求导和原理和softmax一样, 其中 $p_{ji}$ 已知值

2.3 softmax 导数回顾

$\hat{y_i}=\frac{e^{z_i}}{\sum_{j=1}^{k}e^{z_j}}$

损失函数

$J=-\sum_{i}y_ilog\hat{y_i}$

梯度为(one-hot 编码）

$\bigtriangledown z_i=\hat{y_i}-y_i$

2.4 微分方法

根据softmax 求导我们先固定 $\sum_j$

$\frac{\partial J}{\partial z_i}= \sum_j (q_{ij}-p_{ij})$

则

$\frac{\partial J}{\partial a_i}= \frac{\partial J}{\partial z_i} \frac{\partial z_i}{\partial a_i}$

$=2\sum_j(q_{ij}-p_{ij})(a_i-a_j)$

同样固定 $\sum_i$

$\frac{\partial J}{\partial a_i}=\sum_i(p_{ij}-q_{ij})(a_i-a_j)$

两者相加

$\frac{\partial J}{\partial a_i}=\sum_i(p_{ij}-q_{ij}+p_{ji}-q_{ji})(a_i-a_j)$

三 T-SNE

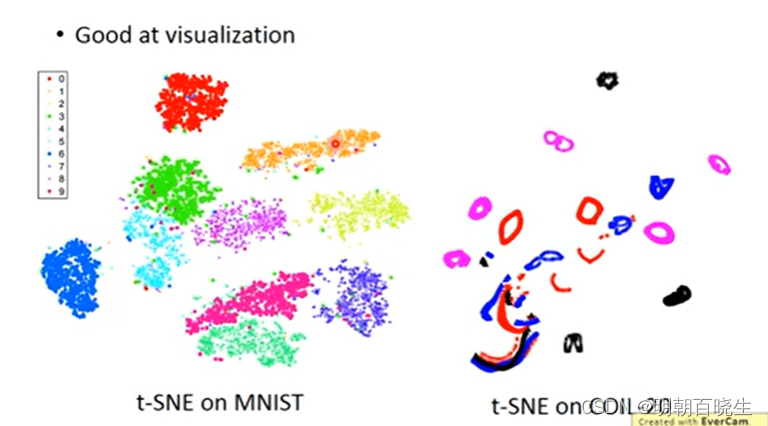
t-SNE中的“t-分布”是一种特殊的概率分布函数，它在低维空间中有利于保留局部结构，同时对于远离的数据点，它会赋予较大的权重。这有助于在低维空间中更好地展示数据的结构。

t-SNE 概率分布改为用t 分布

$q_{ij}=\frac{1+||a_i-a_j||_2^{-1}}{\sum_{k}(1+||a_i-a_k||_2^{-1})}$

微分

$\frac{\partial J }{\partial a_i}=4 \sum_j (p_{ij}-q_{ij})(a_i-a_j)(1+||a_i-a_j||_2^{-1})^{-1}$

四 Python 代码

# -*- coding: utf-8 -*-
"""
Created on Mon Feb 19 17:55:14 2024@author: chengxf2
"""from sklearn.manifold import TSNE
from sklearn.datasets import load_iris
from sklearn.datasets import load_digits
import matplotlib.pyplot as pltdef load_digit():# 导入一个手写数据集（比MNIST数据集小），每个数据点是0-9的一张8*8灰度图像print("\n --load data--")digits = load_digits()X = digits.dataY = digits.targetprint("\n X:", X.shape)print("\n Y",Y.shape)return X,Ydef load_iris():'''Iris数据集是常用的分类实验数据集，由Fisher, 1936收集整理。Iris也称鸢尾花卉数据集，是一类多重变量分析的数据集。数据集包含150个数据样本，分为3类，每类50个数据，每个数据包含4个属性。可通过花萼长度，花萼宽度，花瓣长度，花瓣宽度4个属性预测鸢尾花卉属于（Setosa，Versicolour，Virginica）三个种类中的哪一类。Returns-------None.'''    iris = load_iris()X = iris.dataY = iris.targetprint("\n X:", X.shape)print("\n Y",Y.shape)return X,Ydef t_SNE(X,Y):'''n_components:  降维后的维度，默认为2perplexixity:   默认为30，较大值会使得随机选择的领域更大n_iter : 迭代次数，默认1000init: 默认随机初始化'''tsne = TSNE(n_components=2, n_iter=1000).fit_transform(X)plt.subplot(121)plt.scatter(tsne[:, 0], tsne[:, 1], c=Y)plt.colorbar()plt.show()if __name__ == "__main__":print("\n ---enter---")X,Y = load_digit()print("\n ---降维----")t_SNE(X,Y)

参考：

15: Unsupervised Learning - Neighbor Embedding_哔哩哔哩_bilibili

https://www.cnblogs.com/501731wyb/p/16014141.html

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://xiahunao.cn/news/2803496.html

如若内容造成侵权/违法违规/事实不符，请联系瞎胡闹网进行投诉反馈，一经查实，立即删除！