一、逻辑函数的标准与或式和最简式
1、标准与或表达式
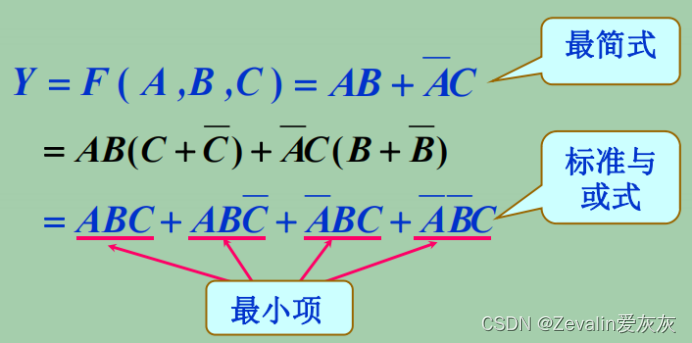
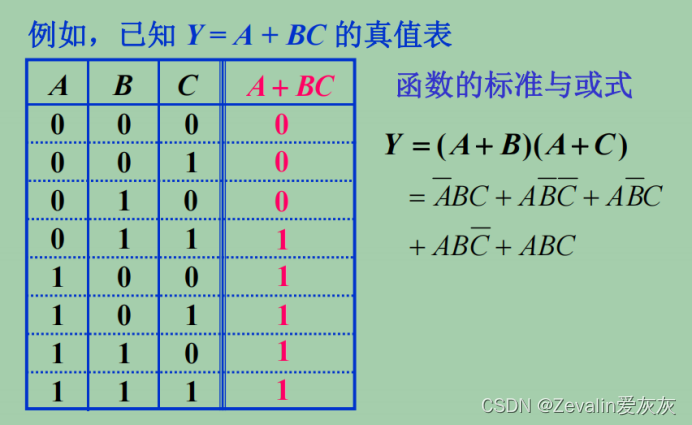
(1)下图给出了逻辑函数Y的标准与或表达式,在表达式中每一个乘积项都具有标准形式,这种标准形式的乘积项称为最小项。
(2)最小项是逻辑代数中的一个重要概念,下图中Y是变量A、B、C的函数,三个变量可以构成8个标准形式的乘积项(、
、
、
、
、
、
、
),这8个乘积项的共同特点是:
①每个乘积项都有3个因子。
②每一个变量都以原变量或者反变量的形式,作为一个因子在乘积项中出现且仅出现一次。
(3)对于n个变量,如果P是一个含有n个因子的乘积项,而且每一个变量都以原变量或者反变量的形式作为一个因子在P中出现且仅出现一次,那么就称P是这n个变量的一个最小项。n个变量一共有个最小项,因为每一个变量都有原变量、反变量两种形式,变量个数是n。

(4)最小项的性质:
①每一个最小项都有一组且只有一组使其值为1的对应变量取值。
②任意两个不同的最小项之积,值恒为0。
③变量全部最小项之和,值恒为1。
(5)任何逻辑函数都可以表示成为最小项之和的形式——标准与或表达式,也就是说,任何逻辑函数都是由函数中变量的若干个最小项构成的。
(6)逻辑函数最小项之和的形式——标准与或表达式是唯一的,也就是说,一个逻辑函数只有一个最小项之和的表达式。
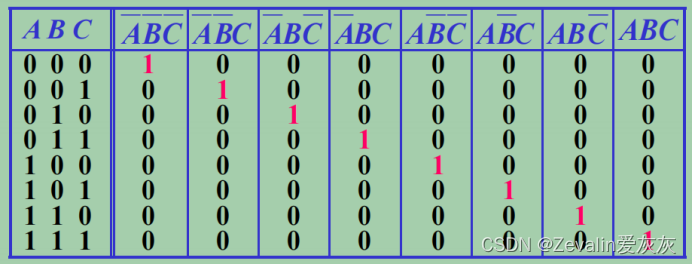
(7)逻辑函数的标准与或表达式也可以从真值表中直接得到,只要在真值表中挑出那些使函数值为1的变量取值,变量取值为1的写出原变量,为0的写成反变量,这样对应于使函数值为1的每一种取值都可以写出一个乘积项,只要把这些乘积项加起来,得到的就是函数的标准与或表达式。
(8)为了叙述和书写的方便,通常都要对最小项进行编号,把与最小项对应的变量取值当成二进制数,与之相应的十进制数就是该最小项的编号,用表示。(一个最小项,只要把原变量当成1、反变量当成0,便可直接得到它的编号)

2、逻辑函数的最简表达式
(1)最简与或式:乘积项的个数最少,每个乘积项中相乘的变量个数也最少的与或表达式。
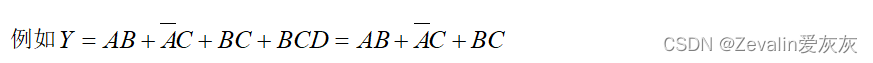
(2)最简与非—与非式:非号最少(单个变量上面的非号不算),每个非号下面相乘的变量个数也最少的与非-与非式。(在最简与或表达式的基础上,两次取反,再用德·摩根定理去掉下面的反号,便可得到函数的最简与非—与非表达式)
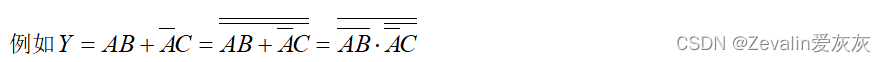
(3)最简或与式:括号个数最少,每个括号中相加的变量的个数也最少的或与式。(在反函数最简与或表达式的基础上,取反,再用德·摩根定理去掉下面的反号,便可得到函数的最简或与式)
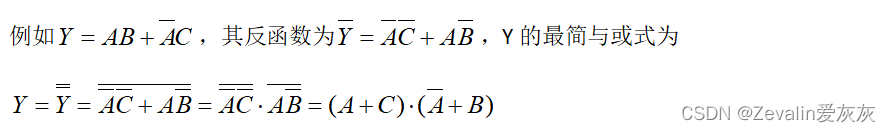
(4)最简或非—或非式:非号个数最少,非号下面相加的变量个数也最少的或非—或非式。(在最简或与表达式的基础上,两次取反,再用德·摩根定理去掉下面的反号,便可得到函数的最简或非—或非式)
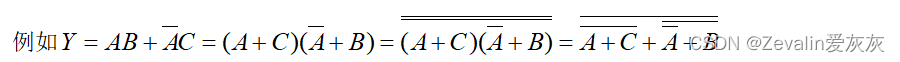
(5)最简与或非式:非号下面相加的乘积项的个数最少,每个乘积项中相乘的变量个数也最少的与或非式。(在最简或非—或非表达式的基础上,用德·摩根定理去掉下面的反号,便可得到函数的最简与或非式)
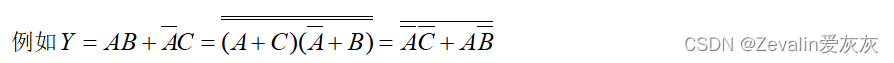
二、逻辑函数的公式化简法
1、并项法
(1)做法:利用公式把两个乘积项合并起来,消去一个变量。
(2)举例:
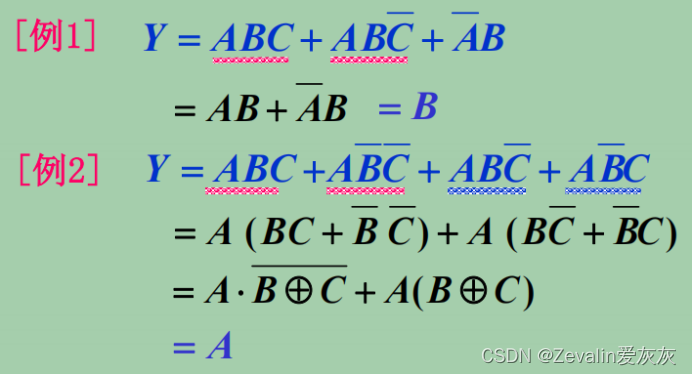
2、吸收法
(1)做法利用公式吸收掉多余的乘积项。
(2)举例:
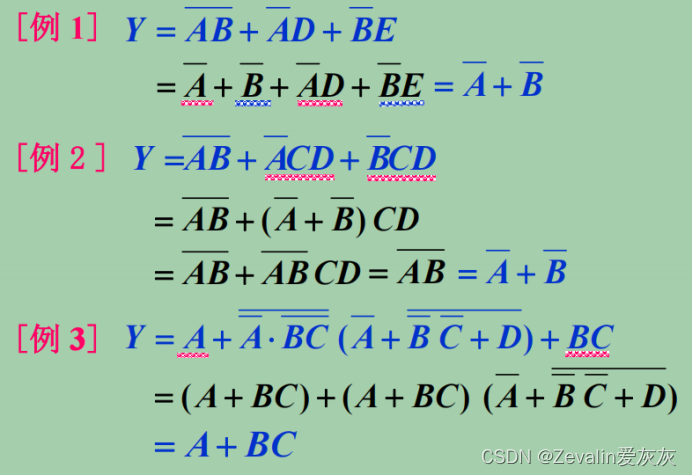
3、消去法
(1)做法:利用公式消去乘积项中多余的因子。
(2)举例:
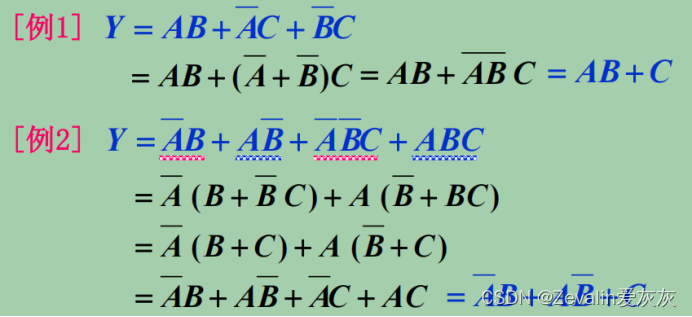
4、配项消项法
(1)做法:利用公式在函数与或表达式中加上多余项(冗余项),以消去更多的乘积项。
(2)举例:
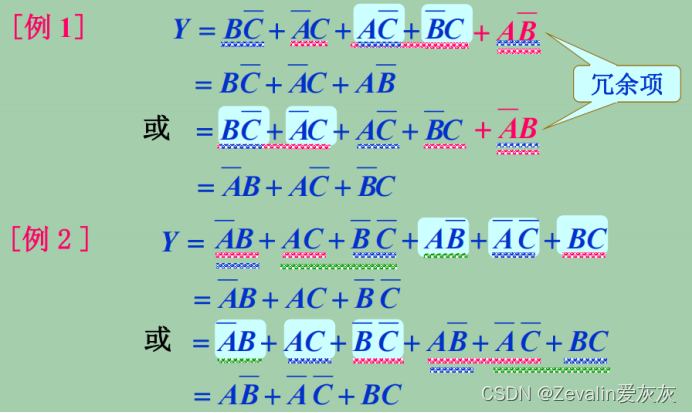
三、逻辑函数的图形化简法
1、图形化简法概述
(1)卡诺图即最小项方格图,用卡诺图化简逻辑函数,求最简与或表达式的方法,称为图形化简法。
(2)图形化简法有比较明确的步骤可以遵循,结果是否最简,判断起来也比较容易,但是当变量个数较多时,这种方法也会变得麻烦。
2、逻辑变量的卡诺图
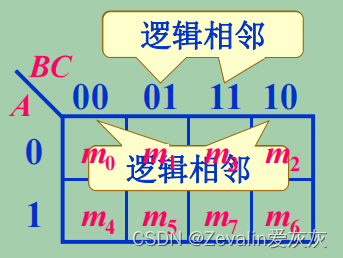
(1)二变量的卡诺图(4个最小项):
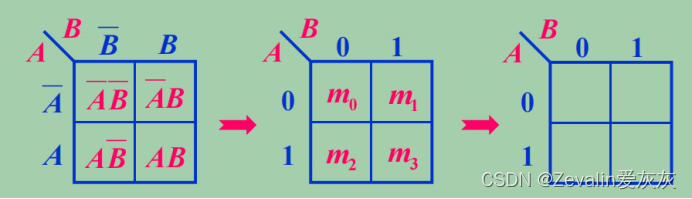
(2)变量卡诺图的画法:
①变量卡诺图一般都画成正方形或矩形。对于n个变量,图中分割出的小方块应有个,因为n个变量有
个最小项,而每一个最小项都需要用一个小方块表示。
②按循环码排列变量取值顺序。循环码的特点是相邻编码之间只有1位码元不同,这是关键,只有这样排列,所得到的最小项方块图才成为卡诺图。
[1]循环码可以很容易地由自然二进制码推导出来,二进制码为则对循环码
(这里先用二进制表示)有
(
)。
[2]实际上并不用记住上面给出的规律,把卡诺图画出来后,每个小方块都对应一个最小项,把最小项对应的二进制数转换为十进制数,就是该方块的循环码。
(3)变量卡诺图的特点:
①在卡诺图中,凡是几何相邻的最小项,在逻辑上都是相邻的。
[1]几何相邻:方块几何相邻有三种情况,一是相接(紧挨着),二是相对(任一行或一列的两头),三是相重(卡诺图对折起来后位置重合)。
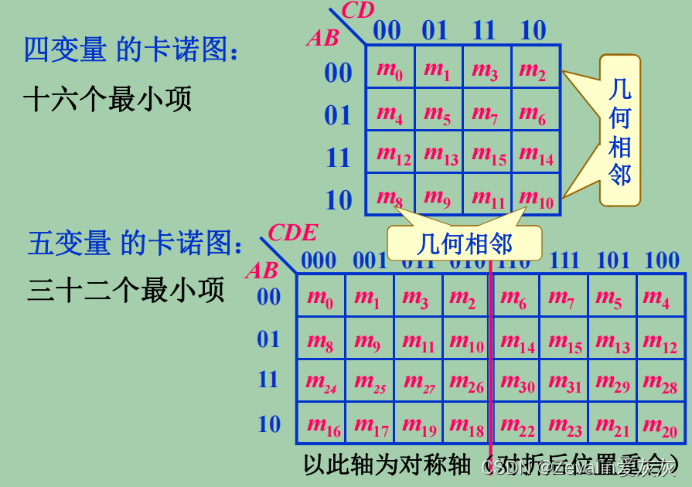
[2]逻辑相邻:如果两个最小项,除了一个变量的形式不同以外,其余的都相同,那么这两个最小项就称为在逻辑上是相邻的,而在逻辑上相邻的最小项是可以合并的(合并之后能消去至少一个因子)。
②卡诺图的主要缺点是随着变量个数的增加,图形会越来越复杂,当变量多于6个时,卡诺图将会变得非常庞大,不好处理。
(4)变量卡诺图中最小项合并的规律:
①两个相邻最小项合并可以消去一个因子。
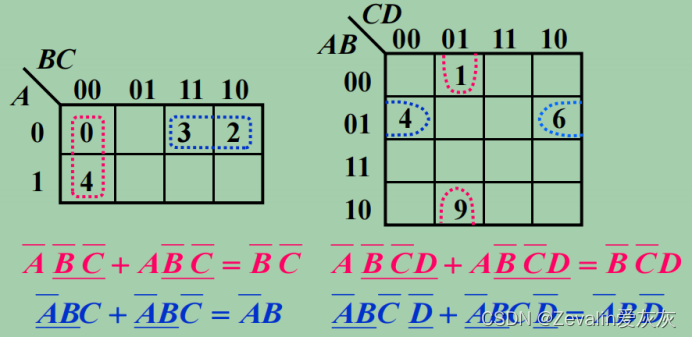
②四个相邻最小项合并可以消去两个因子。
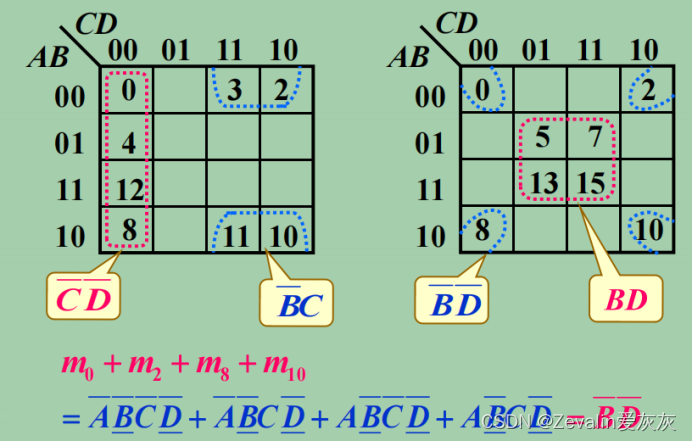
③八个相邻最小项合并可以消去三个因子。
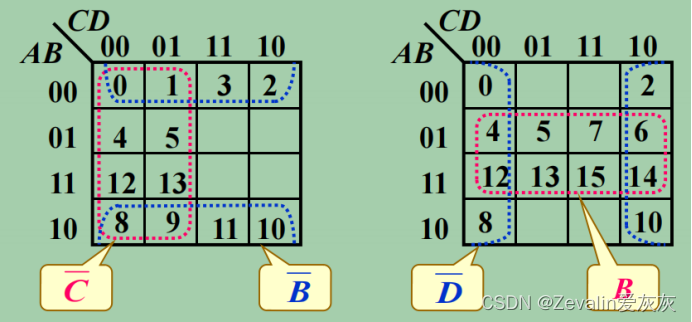
④个相邻最小项合并可以消去n个因子。
3、逻辑函数的卡诺图
(1)逻辑函数卡诺图的画法:
①根据函数的变量个数画出相应的卡诺图。
②在函数的每一个乘积项所包含的最小项处都填1,其余位置填0或不填。
(2)逻辑函数卡诺图的特点:
①优点:用几何位置的相邻,形象地表达了构成函数的各个最小项在逻辑上的相邻性。
②缺点:当函数变量多于六个时,画图十分麻烦,其优点不复存在,无实用价值。
(3)逻辑函数卡诺图画法举例:(下图中未给出标准与或表达式,最小项需要根据非标准式自己推断)

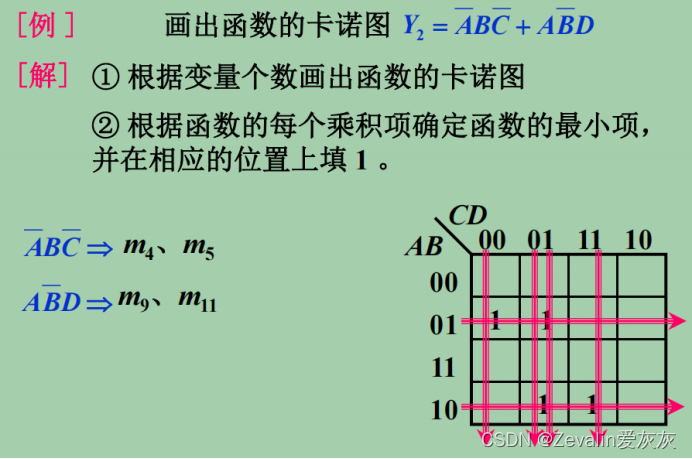
(4)用卡诺图化简逻辑函数:
①基本步骤:画出逻辑函数的卡诺图,合并逻辑函数的最小项,选择乘积项写出最简与或式。
②合并最小项的原则:
[1]必须包含函数的所有最小项(最好先圈出孤立项),并且保证合并后乘积项的总数最少(也就是圈圈的个数越少越好,这需要尽可能地把包围圈画到最大)。
[2]相邻的最小项合并时,蕴含函数的最小项数量越多,则合并后乘积项的因子越少,(i=0,1,2,…,n-1)个相邻的最小项相或,可以消去i个变量。
[3]每次合并时,为了消去更多变量,可以重复使用函数的最小项,但是必须保证至少包含1个新的最小项(也就是未被重复使用过的最小项),以避免冗余项的出现。
③举例:
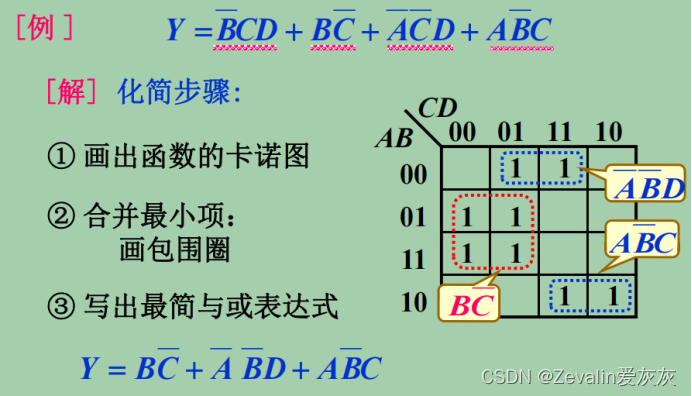
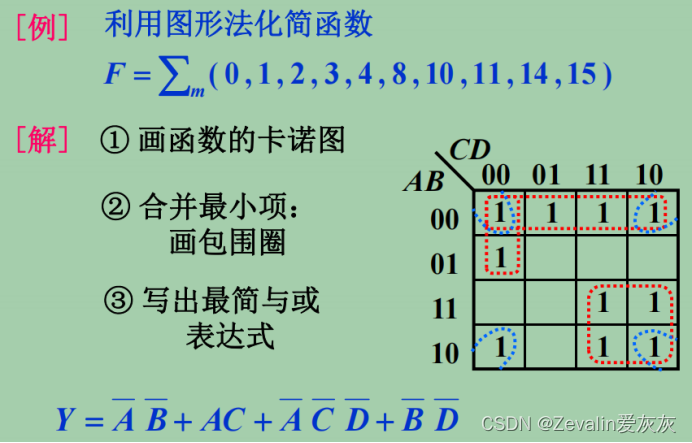
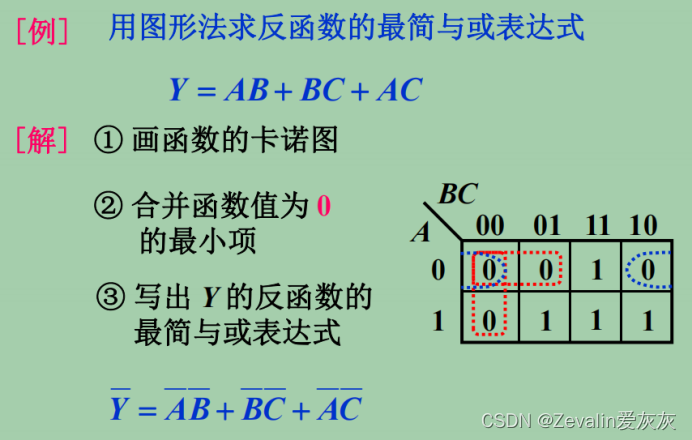
四、具有约束的逻辑函数的化简
1、约束的概念和约束条件
(1)约束:
①约束即输入变量取值所受的限制。
②举例:逻辑变量A、B、C分别表示电梯的升、降、停命令,A = 1表示升,B = 1表示降,C = 1表示停。
| ABC的可能取值 | 001、010、100 |
| ABC的不可能取值 | 000、011、110、101、111 |
(2)约束项:不会出现的变量取值所对应的最小项。
(3)约束条件:
①由约束项相加所构成的值为0的逻辑表达式就是约束条件。
②约束条件的表示方法:
[1]在真值表和卡诺图上用叉号(×)表示。
[2]在逻辑表达式中,用等于0的条件等式表示。

2、具有约束的逻辑函数化简
(1)约束条件在化简中的应用:
①在公式法中,可以根据化简的需要加上或去掉约束条件,因为在逻辑表达式中,加上或去掉0,函数是不会受到影响的,而约束条件的值总是为0。

②在利用函数的卡诺图合并最小项时,可根据化简的需要包含或去掉约束项,因为合并最小项时,如果圈中包含了约束项,则相当于在相应的乘积项中加上了该约束项(其值为0),函数不会受到影响(但这并不意味着要把所有约束项都包含进去,约束项在化简中的作用仅仅只是可以使包围圈更大,而不是使包围圈的个数变多)。

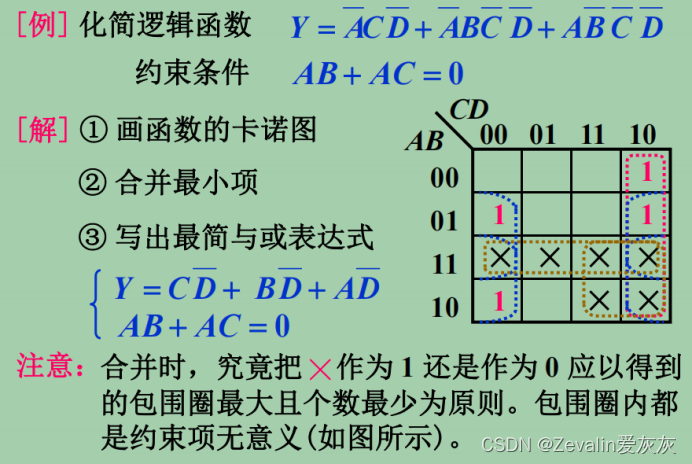
(2)变量互相排斥的逻辑函数的化简:
在一组变量中,只要有一个变量取值为1,则其它变量的值就一定是0,有这种约束的变量称为互相排斥的变量。

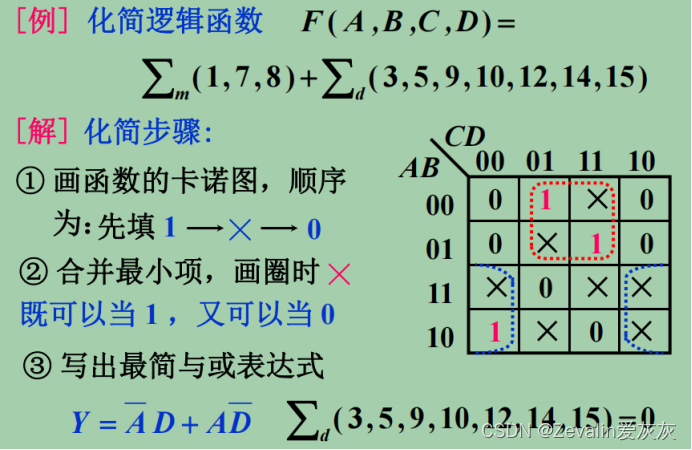
3、化简举例