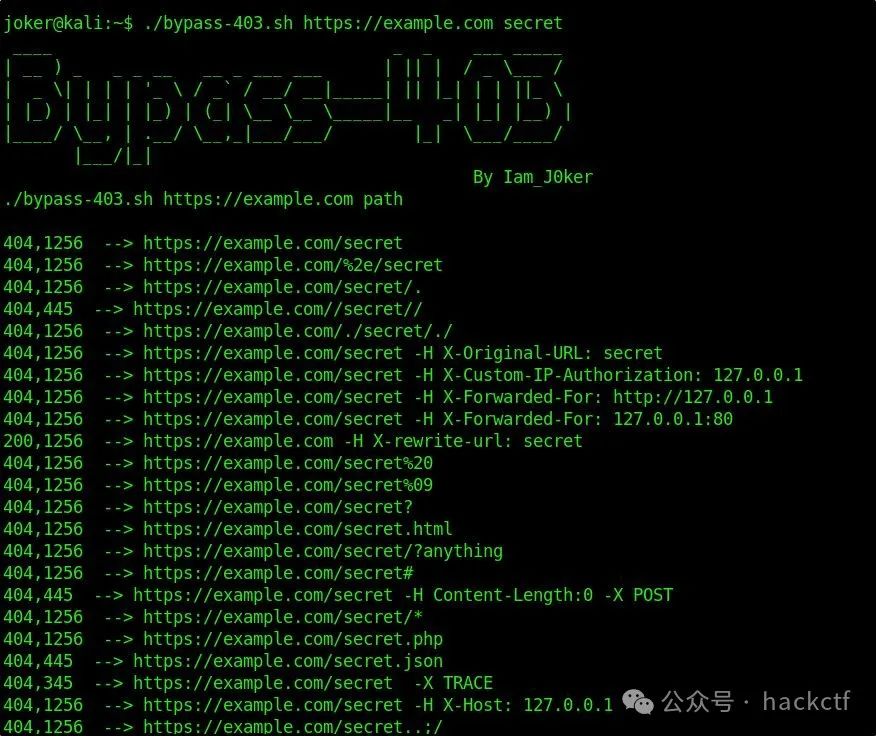
题目

给出正整数n，要求按如下方式构造数列：

1. 只有一个数字n的数列是一个合法的数列。
2. 在一个合法的数列的末尾加入一个正整数，但是这个正整数不能超过该数列最后一项的一半，可以得到一个新的合法数列。

请你求出，一共有多少个合法的数列。两个合法数列a,b不同当且仅当两数列长度不同或存在一个正整数i≤∣a∣，使得​。

输入输出格式

输入格式

输入只有一行一个整数，表示n。

输出格式

输出一行一个整数，表示合法的数列个数。

输入输出样例

输入样例

6

输出样例

6

解析

对于一个整数n，如果只考虑变换一次，那么问题就很简单了，答案就是n/2+1，但是还需要对变换后的继续变换。比如说，数列中最开始只有一个元素8，在末尾加入一个新元素，列表就可以变成[8 4]、[8 3]、[8 2]、[8 1]，算上[8]一共有五种情况，之后的变换只需要按照上面的这种方法，分别是计算[4]、[3]、[2]、[1]按照这样的操作能有几种情况，然后累加统计即可。

原来是要解决n=8的问题，现在分解成了4个规模更小但本质上同样的子问题；如果要解决n=4的问题，基于同样的思想还可以分解成两个规模更小的单质相同的子问题；当需要解决n=2的问题时，可以分解成n=1的问题（只有n=1的情况了）；直到n=1时，没法继续分解，根据题目说的“不作任何处理就直接统计为一种合法的数列”，可以直接返回只有唯一一种数列，即[1]。然后返回上一层接受到所有小规模问题的答案，合并统计处理获得这个规模下的答案，再继续返回上一层……直到求得问题的解。

像这样构造函数，这个函数在运行过程中调用自己，从而解决问题的思路就称为递归思想。

#include<iostream>
#include<cstring>
using namespace std;
int n,count,f[1010];
int sol(int x){int count=1;if(f[x]!=-1){return f[x];}for(int i=1;i<=x/2;i++){count+=sol(i);}return f[x]=count;
}
int main(){cin>>n;memset(f,-1,sizeof(f));f[1]=1;cout<<sol(n)<<endl;return 0;
}

直接使用递归运行效率很低，为了防止做很多无用功，可以定义一个数组f，其每一项f[i]就是当问题规模为i的时候的答案，首先将数组初始化为-1，说明f[i]还没有被计算过。依然使用同样的方法去求解，只是如果发现已经计算过就直接返回f[i]，而不必进行接下来的计算了，否则还是按照刚才递归的方式计算，然后将结果存入数组中以便之后再次调用。

这样，每个数字最多只计算一次，因为一旦计算完成就会被存下来，便于日后使用，这样的思想称为“记忆化搜索”。