一、数论
(一)判断质数
1、质数合数都是针对>=2的整数
2、质数的判断
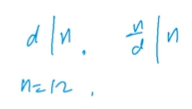
一些因数的判断是不必要的。
#include<bits/stdc++.h>
//判断素数O(n^0.5)
using namespace std;
int n;
bool is_Prime(int n)
{if(n<2)return false;for(int i=2;i<n/i;i++){if(n%i==0)return false;}return true;
}
int main()
{cin>>n;if(is_Prime(n))puts("Yes");else puts("No");
}
(二)分解质因数和求(0~N)内的所有质数
1、初等方法(朴素方法)
(1) 因为n最多只有一个大于sqrt(n)的因子。可以和质数判断一样,n/i为条件进行迭代。
最后如果n>1,剩下的就是最后的因子(大于sqrt(n)的数)。如果等于1,那么在前面的循环中已经找到所有的因子将其除掉了。
最好O(lg(n)):当n是某个质数的整数次方的时候
#include<bits/stdc++.h>
//求解质因数869
using namespace std;
int n;
void divide(int x)
{for(int i=2;i<=n/i;i++){if(n%i==0){int res=0;while(n%i==0){n/=i;res++;}cout<<i<<" "<<res<<endl;}}if(n>1)cout<<n<<" "<<1<<endl;
}
int main()
{cin>>n;divide(n);return 0;
}
(2)分析时间复杂度
当进行n次循环的时候,i=2的时候需要n/2次循环,依此类推,得到时间复杂度为O(n ln n)<O(n log n)。

2、(埃氏筛法)优化方法:只需要把所有的质数的倍数筛掉
按照之前的方法筛选的时候留下的都是质数,观察可以看到被筛掉的合数可以只通过前面的质数筛掉。根据质数原理:0~n之间的质数的个数为 n/ln(n) 。所以可以在之前的时间复杂度上除以一个ln(n),结果为O(n log( log n))

这样从小到大的筛法,将迭代到的所有的数的倍数都处理掉之后,每次遇到的还未被消掉的就是素数。
#include<bits/stdc++.h>
//筛选质数
using namespace std;
const int N=1e6+10;
int n,idx;
bool st[N];//是否被消除掉
int res[N];//保存质数
void divide(int x)
{for(int i=2;i<=n;i++)//前面的将其倍数全部删除之后,每次迭代到的st为false就是素数{if(!st[i]){res[idx++]=i;//消除掉所有的倍数。for(int j=i+i;j<=n;j+=i)st[j]=true;}}
}
int main()
{cin>>n;divide(n);for(int i=0;i<idx;i++)cout<<res[i]<<" ";return 0;
}
3、线性筛法(只会被自己的最小质因子筛掉))
是埃氏筛法(一个合数可能会被多个质数筛掉)的优化,

对于每一个数,从小到大遍历所有的质数,让每个数只被自己的最小质因数筛掉,只要找到第一个质数可以将某数删掉。
每一次循环先判断这个数有没有被筛掉过,没有被筛掉过,就保存当前数到数组。不管当前的i是不是素数,都让目前所有的素数从小到大依次乘以i。由于i是从1到2遍历。所以某个数总是被其最小质因子筛掉。
在埃氏筛法的基础上的优化位置是if(i%res[j]==0)break;
prime数组中的素数是递增的,当 i 能整除 prime[j],那么 i*prime[j+1] 这个合数肯定也可以被 prime[j] 筛掉,因为i中含有prime[j], prime[j] 比 prime[j+1] 小。
我们没有必要让prime[j+1]去筛掉prime[j+1]*i,因为由于……==0,在后面一定存在一个i,使得prime[j]*i将其删掉。后面所有的Prime[j+……] 都是这样。
#include<bits/stdc++.h>
//筛选质数(线性筛法)
using namespace std;
const int N=1e6+10;
int n,idx;
bool st[N];//是否被消除掉
int res[N];//保存质数
void divide(int x)
{for(int i=2;i<=n;i++){if(!st[i])res[idx++]=i;//从小到大遍历所有质数for(int j=0;res[j]<=n/i;j++)//设置边界,避免超出n{st[res[j]*i]=true;//让当前所有的质数乘以同一个数的结果筛掉if(i%res[j]==0)break;//res[j]一定是i的最小质因子//也一定是res[j]*i的}}
}
int main()
{cin>>n;divide(n);for(int i=0;i<idx;i++)cout<<res[i]<<" ";return 0;
}
(三)求约数的值和约数的个数和所有约数的和


1、求一个整数的所有约数
#include<bits/stdc++.h>
//868 式除法求约数
using namespace std;
const int N=1e6+10;vector<int>get_divisor(int n)
{vector<int>ans;for(int i=1;i<n/i;i++){if(n%i==0){ans.push_back(i);if(i!=n/i)ans.push_back(n/i);}}sort(ans.begin(),ans.end());return ans;
}
int main()
{int x;cin>>x;auto res=get_divisor(x);for(auto x:res)cout<<x<<" ";
}
2、求约数的个数
求一组数的乘积的约数的个数:将每个数分解质因数,使用map存储;
#include<bits/stdc++.h>
//868 除法求约数个数using namespace std;
typedef long long LL;
const int N=1e9+7;
int main()
{int n;LL ans=1;cin>>n;unordered_map<int,int>hash;while(n--){int x;cin>>x;for(int i=2;i<=x-i;i++){while(x%i==0){hash[i]++;x/=i;}}if(x>1)hash[x]++;}for(auto p: hash)ans=ans*(p.second+1)%N;cout<<ans<<endl;
}
3、求所有约数的和
同样用hash保存底数和对应的指数。while(b--)循环求取不同底数的等差数列的和。将所有的数相乘。
#include<bits/stdc++.h>
//求所有约数的和
using namespace std;
typedef long long LL;
const int N=1e9+7;
int main()
{int n;LL res=1;cin>>n;unordered_map<int,int>hash;while(n--){int x;cin>>x;for(int i=2;i<=x-i;i++){while(x%i==0){hash[i]++;//同样用哈希表保存数x/=i;}}if(x>1)hash[x]++;}for(auto p: hash){LL a=p.first,b=p.second;//a为底数,b为指数LL t=1;while(b--)t=(t*a+1)%N;res=res*t%N;}cout<<res<<endl;
}
(四)欧几里得算法
(a,b)的所有公约数约数的集合,与(b,a mod b)的公约数的集合完全一致。
可知最大公约数也完全相同。
根据这一等价代换的方法,可以一直进行这样的 代换,直到 b=0的时候,直接返回a即可。
#include<bits/stdc++.h>
//求一对数的最大公约数
using namespace std;
typedef long long LL;
const int N=1e9+7;
int gcd(int a,int b)
{return b ?gcd(b,a % b):a;
}
int main()
{int n;cin>>n;while(n--){int a,b;cin>>a>>b;int ans=gcd(a,b);cout<<ans<<endl;}
}
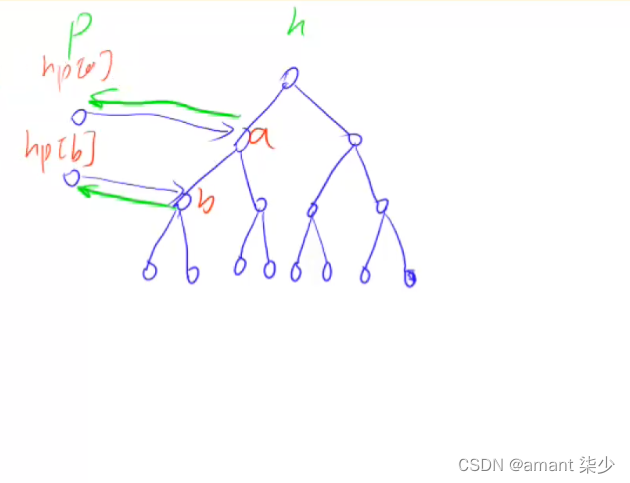








![[数学]高斯消元](https://img-blog.csdnimg.cn/direct/be179525c34c48c0832beb4aa4b0dc68.png)