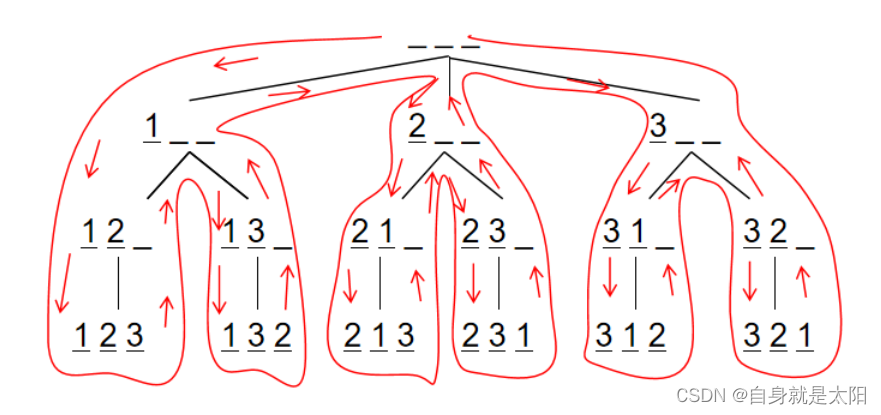
春晚的魔术实际上是一个约瑟夫问题,最终的结果是魔术开始时确定的几个变量确定好的,扑克牌只是道具和障眼法。网上一查这个问题发现颇有历史渊源,17世纪的法国数学家加斯帕在《数目的游戏问题》中讲了这样一个故事:15个教徒和15 个非教徒在深海上遇险,必须将一半的人投入海中,其余的人才能幸免于难,于是想了一个办法:30个人围成一圆圈,从第一个人开始依次报数,每数到第九个人就将他扔入大海,如此循环进行直到仅余15个人为止。问怎样排法,才能使每次投入大海的都是非教徒。
编程实现这个过程:
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>int main(void)
{int n, m, i, kill = 0, t = 0, s = 0;scanf("%d %d", &n, &m);printf("%s line %d, total object %d, kill every %d object.\n",__func__, __LINE__, n, m);// the first object are reserved, the first index start from// 1, end to n.bool *array = malloc(sizeof(bool) * (n + 1));if (array == NULL) {printf("%s line %d, alloc object buffer failure.\n",__func__, __LINE__);return -1;}for (i = 0; i < (n+1); i ++) {array[i] = false;}do {++t;if (t > n)t = 1; if (!array[t])s++;if (s == m) {s = 0;printf("%d ", t);// kill this object.array[t] = true;kill++;}} while (kill != n); // all has been killed.printf("kill %d object.\n", kill);free(array);return 0;
}
可见杀戮顺序是9 18 27 6 16 26 7 19 30 12 24 8 22 5 23 11 29 17 10 2 28 25 1 4 15 13 14 3 20 21,所以只要保证9 18 27 6 16 26 7 19 30 12 24 8 22 5 23位置上的人都是非教徒,则15名教徒能够全部存活下来。

所以,只要把非教徒安排在5,6,7,8,9,12,16,18,19,22,23,24,26,27,30位置上,能够达到仅杀死非教徒的目的。