糖尿病数据线性回归预测

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_diabetes
diabetes=load_diabetes()
data=diabetes['data']
target=diabetes['target']
feature_names=diabetes['feature_names']
data.shape
df = pd.DataFrame(data, columns=feature_names)
df.head()
# 抽取训练数据和预测数据
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test=train_test_split(data,target,test_size=0.2)
x_train.shape,x_test.shape
# 创建模型
from sklearn.linear_model import LinearRegression
linear=LinearRegression()
linear.fit(x_train,y_train)
# 预测
y_pred=linear.predict(x_test)
y_pred
# 得分: 回归的得分很低
#linear.score(x_test,y_test)
### 线性回归评估指标
#- mean_squared_error 均方误差
from sklearn.metrics import mean_squared_error as mse
# 均方误差
mse(y_test,y_pred)
#### 求线性方程: y = WX + b 中的W系数和截距b
# w系数
linear.coef_
# 10个特征 就有10个系数
# b截距
linear.intercept_
#### 研究每个特征和标记结果之间的关系.来分析哪些特征对结果影响较大
plt.figure(figsize=(5*4, 2*4))for i, col in enumerate(df.columns):# 每一列数据data2 = df[col].copy()# 画子图ax = plt.subplot(2, 5, i+1)ax.scatter(data2, target)# 线性回归：对每一个特征进行回归分析linear2 = LinearRegression()linear2.fit(df[[col]], target)# 每个特征的系数w和截距b# y = wx + bw = linear2.coef_[0]b = linear2.intercept_# print(w, b)# 画直线x = np.linspace(data2.min(), data2.max(), 2)y = w * x + bax.plot(x, y, c='r')# 特征score = linear2.score(df[[col]], target)  # 模型得分ax.set_title(f'{col}: {round(score, 3)}', fontsize=16)

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
### 抛物线函数
# 抛物线函数
# f(x) = (x - 2)²  + 5# Python函数
f=lambda x:(x-2)**2+5
# 画图
x=np.linspace(-2,6,100)
y=f(x)
plt.plot(x,y)
#### 使用梯度下降算法 求 当x为多少时，函数f(x)的值最小
# ①对目标函数求导； 
# ②循环对参数更新;
# ①对目标函数求导； # 抛物线函数
# f(x) = (x - 2)²  + 5# 求导数
#  dx = 2x - 4
d = lambda x: 2 * x - 4
# ②循环对参数更新;
θ = 6
# 学习率 lr  : learning_rate 
lr=0.03
# 最大迭代次数
max_iter=100
θ_list = [θ]
# 循环
for i in range(max_iter):θ = θ - lr * d(θ)θ_list.append(θ)
θ_array = np.array(θ_list)
# 画图
x=np.linspace(-2,6,100)
y=f(x)
plt.figure(figsize=(4,5))
plt.plot(x,y)
plt.plot(θ_array,f(θ_array), marker='*')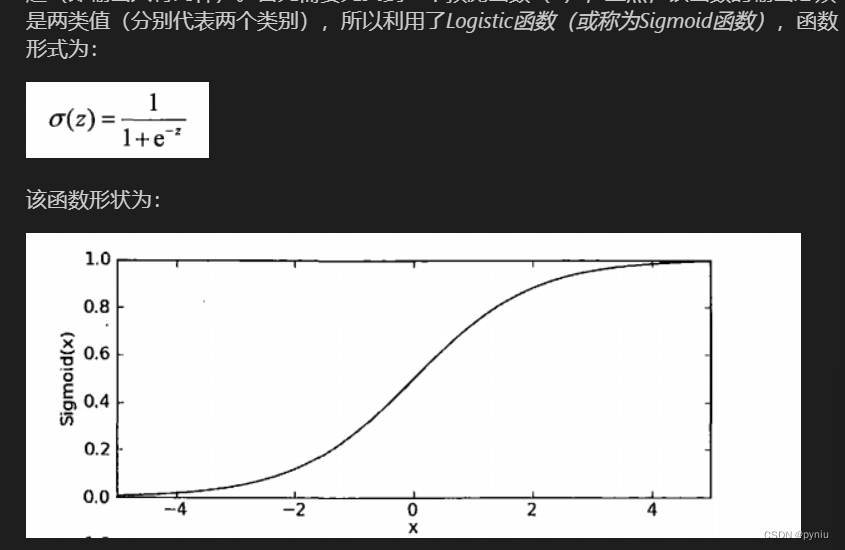

Logistic Regression虽然名字里带“回归”，但是它实际上是一种分类方法，用于两分类问题（即输出只有两种）。首先需要先找到一个预测函数（h），显然，该函数的输出必须是两类值（分别代表两个类别），所以利用了*Logistic函数（或称为Sigmoid函数）*

#1实战手写数字识别
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# 逻辑回归: 分类
from sklearn.linear_model import LogisticRegression
# 使用KNN与Logistic回归两种方法
from sklearn.datasets import load_digits
digits=load_digits()
digits
data=digits['data']
target=digits['target']
feature_names=digits['feature_names']
target_names=digits['target_names']
imges=digits['images']
data.shape
imges.shape
pd.Series(target).unique()
feature_names
#划分数据集
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(data, target, test_size=0.2)
#使用逻辑回归
#创建模型，训练和预测
# C=1.0 :  越大表示越严格，对训练数据拟合更好，可能导致过拟合
#          越小表示不严格，对训练数据拟合不好，可能导致欠拟合
#
# solver : 逻辑回归的损失函数的一种进行优化的算法
#      {'lbfgs', 'liblinear', 'newton-cg', 'newton-cholesky', 'sag', 'saga'},
#    solver='lbfgs' 默认值
#    liblinear：一般适用于小数据集
#    sag,saga: 一般使用于大数据集，速度更快
#    其他是中等数据集
# 
#  max_iter=100: 最大迭代次数
#  
#  n_jobs=-1  表示使用的CPU核数，多进程处理，一般设置为CPU核数，-1表示时使用所有处理器
lr=LogisticRegression(C=1.0,solver='lbfgs',max_iter=100,n_jobs=-1)
#训练
%timeit lr.fit(x_train,y_train)
# 预测
%timeit lr.predict(x_test)
# 得分
lr.score(x_train,y_train)
lr.score(x_test,y_test)

# 导包使用datasets.make_blobs创建一系列点
#from sklearn.datasets import make_blobs
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import make_blobs
# n_samples=100,  样本数，行数
# n_features=2,   特征数，列数
# centers=None,  几堆点，默认是3
# cluster_std=1.0,  离散程度
data,target=make_blobs(n_samples=300,centers=4,cluster_std=1.0)
plt.scatter(data[:,0],data[:,1],c=target)
#设置三个中心点，随机创建100个点
#创建机器学习模型(逻辑斯蒂回归)，训练数据
lr=LogisticRegression(max_iter=10000)  
lr.fit(data,target)
lr.score(data,target)
#分类后，并绘制边界图
x=np.array([1,2,3,4])
y=np.array([5,6,7,8,9])
X, Y = np.meshgrid(x, y)
# 让X，Y相交
XY=np.c_[X.reshape(-1),Y.reshape(-1)]
#  分别对x轴和y轴的数据等分成1000份
#  分别对x轴和y轴的数据等分成1000份
x = np.linspace(data[:, 0].min(), data[:, 0].max(), 1000)
y = np.linspace(data[:, 1].min(), data[:, 1].max(), 1000)X, Y = np.meshgrid(x, y)# ravel()： 扁平化
XY = np.c_[X.ravel(), Y.ravel()]
XY.shape
# 提供测试数据： XY
y_pred=lr.predict(XY)
y_pred.shape
# 画边界图
plt.pcolormesh(X,Y,y_pred.reshape(1000,1000))
plt.scatter(data[:,0],data[:,1],c=target,cmap='rainbow')