进入人工智能领域免不了与算法打交道，算法依托数学基础，很多小伙伴可能新生畏惧，不用怕，算法没那么难，也没那么玄乎，未来人工智能时代说不得人人都要了解算法、应用算法。

本文试图以一篇文章，用程序演绎的方式给大家把这里面的数学基础先讲清楚，以便于咱们未来深入，呵呵。

第一次接触机器学习的小伙伴，环境搭建参考我的这篇文章（只参考这个里面关于环境搭建的部分就可以）：

政安晨的机器学习笔记——跟着演练快速理解TensorFlow（适合新手入门）https://blog.csdn.net/snowdenkeke/article/details/135950931

环境准备好之后，我们开始！

导入目标

机器学习中，那些“机器”学习的是什么？——数据。学习到的是什么？——模式和规律（或者说是可以解决实际问题的模型）。

详细点说，就是这样：

这些模式和规律可以用来预测未来的数据，做出决策或识别新的数据。

具体来说，智能程序通过分析大量的输入数据，并根据这些数据中的模式和趋势来训练模型。这些模型可以用来解决各种问题，如图像识别、语音识别、自然语言处理等。通过训练模型，智能程序能够自动从数据中提取特征、学习规律，并根据这些规律做出相应的预测或判断。

from tensorflow.keras.datasets import mnist
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()

咱们导入这个数据集，目标是训练一个神经网络，解决的问题是：将手写数字的灰度图像（28像素×28像素）划分到10个类别中（从0到9）。

我们将使用MNIST数据集，它是机器学习领域的一个经典数据集，其历史几乎和这个领域一样长，而且已被人们深入研究。这个数据集包含60 000张训练图像和10 000张测试图像，由美国国家标准与技术研究院（National Institute of Standards and Technology，即MNIST中的NIST）在20世纪80年代收集而成。

你可以将“解决”MNIST问题看作深度学习的“Hello World”，用来验证你的算法正在按预期运行。

导入数据集之后，用下面截图中的几行代码看一下这个数据集的形状(shape)，确定数据集是OK 的。

这个数据存储在多维NumPy数组中，也叫作张量（tensor）。一般来说，目前所有机器学习系统都使用张量作为基本数据结构。张量对这个领域非常重要，重要到TensorFlow都以它来命名。

张量这一概念的核心在于，它是数据容器。

它包含的数据通常是数值数据，因此它是一个数字容器。你可能对矩阵很熟悉，它是2阶张量。张量是矩阵向任意维度的推广［注意，张量的维度通常叫作轴（axis）］。

标量（0阶张量）

仅包含一个数字的张量叫作标量（scalar），也叫标量张量、0阶张量或0维张量。在NumPy中，一个float32类型或float64类型的数字就是一个标量张量（或标量数组）。可以用ndim属性来查看NumPy张量的轴的个数。标量张量有0个轴（ndim == 0）。张量轴的个数也叫作阶（rank）。下面是一个NumPy标量。

向量（1阶张量）

数字组成的数组叫作向量（vector），也叫1阶张量或1维张量。1阶张量只有一个轴。下面是一个NumPy向量。

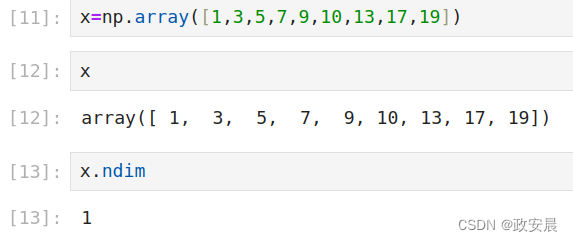
这个向量包含9个元素，所以叫作9维向量。不要把9维向量和9维张量混为一谈！9维向量只有一个轴，沿着这个轴有9个维度，而9维张量有9个轴（沿着每个轴可能有任意个维度）。

维度（dimensionality）既可以表示沿着某个轴上的元素个数（比如9维向量），也可以表示张量的轴的个数（比如9维张量），这有时会令人困惑。对于后一种情况，更准确的术语是9阶张量（张量的阶数即轴的个数），但9维张量这种模糊的说法很常见。

矩阵（2阶张量）

向量组成的数组叫作矩阵（matrix），也叫2阶张量或2维张量。矩阵有2个轴（通常叫作行和列）。你可以将矩阵直观地理解为矩形的数字网格。下面是一个NumPy矩阵。

第一个轴上的元素叫作行（row），第二个轴上的元素叫作列（column）。

在上面的例子中，[5, 78, 2, 34, 0]是x的第一行，[5, 6, 7]是第一列。

3阶张量与更高阶的张量

将多个矩阵打包成一个新的数组，就可以得到一个3阶张量（或称为3维张量），你可以将其直观地理解为数字组成的立方体。下面是一个3阶NumPy张量。

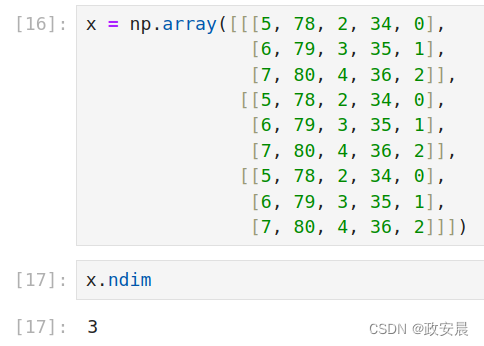
将多个3阶张量打包成一个数组，就可以创建一个4阶张量，以此类推。深度学习处理的一般是0到4阶的张量，但处理视频数据时可能会遇到5阶张量。

关键属性

张量是由以下3个关键属性来定义的。

轴的个数（阶数）。举例来说，3阶张量有3个轴，矩阵有2个轴。这在NumPy或TensorFlow等Python库中也叫张量的ndim。形状。这是一个整数元组，表示张量沿每个轴的维度大小（元素个数）。举例来说，前面的矩阵示例的形状为(3, 5)，3阶张量示例的形状为(3, 3, 5)。向量的形状只包含一个元素，比如(5,)，而标量的形状为空，即()。

数据类型（在Python库中通常叫作dtype）。这是张量中所包含数据的类型。举例来说，张量的类型可以是float16、float32、float64、uint8等。在TensorFlow中，你还可能会遇到string类型的张量。

现在还是回头看一下文章开头，咱们刚刚导入的数据集，下面给出张量train_images的轴的个数，即ndim属性。

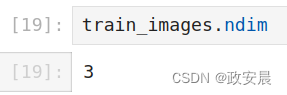
咱们再来看看这个“训练图像数据集”的形状：

下面给出它的数据类型，即dtype属性：

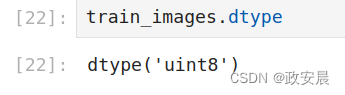
可见，train_images是一个由8位整数组成的3阶张量。

更确切地说，它是由60 000个矩阵组成的数组，每个矩阵由28×28个整数组成。咱们导入的这个数据集中，每个这样的矩阵都是一张灰度图像，元素取值在0和255之间。

我们用Matplotlib库（著名的Python数据可视化库）来显示这个3阶张量中的第7个数字：

代码如下：

import matplotlib.pyplot as plt
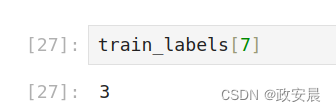
digit = train_images[7]
plt.imshow(digit, cmap=plt.cm.binary)
plt.show()

显而易见，对应的标签是整数3。

在NumPy中操作张量

我们使用语法train_images[i]来沿着第一个轴选择某张数字图像。

选择张量的特定元素叫作张量切片（tensor slicing）。我们来看一下对NumPy数组可以做哪些张量切片运算。下面这个例子选择第10～100个数字（不包括第100个），并将它们放在一个形状为(90, 28, 28)的数组中。

小伙伴们可以使用下列代码尝试一下：

my_slice = train_images[10:100]
my_slice.shape

我的执行演绎如下：

它等同于下面这个更详细的写法——给出切片沿着每个张量轴的起始索引和结束索引。

注意，":" 等同于选择整个轴。

# ----等同于前面的例子
my_slice = train_images[10:100, :, :]
my_slice.shape#----也等同于前面的例子
my_slice = train_images[10:100, 0:28, 0:28]
my_slice.shape

演绎如下：

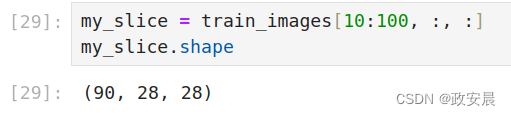
一般来说，可以沿着每个张量轴在任意两个索引之间选择切片。

举例来说，要在所有图像的右下角选出14像素×14像素的区域，可以这么做：

my_slice = train_images[:, 14:, 14:]

也可以使用负数索引。

与Python列表类似，负数索引表示与当前轴终点的相对位置，要在图像中心裁剪出14像素×14像素的区域，可以这么做。

my_slice = train_images[:, 7:-7, 7:-7]

数据批量

通常来说，深度学习中所有数据张量的第一个轴（也就是轴0，因为索引从0开始）都是样本轴[samples axis，有时也叫样本维度（samples dimension）]。在MNIST例子中，样本就是数字图像。

此外，深度学习模型不会一次性处理整个数据集，而是将数据拆分成小批量。具体来看，下面是MNIST数据集的一个批量，批量大小为128。

batch = train_images[:128]

然后是下一个批量：

batch = train_images[128:256]

再然后是第n个批量：

n = 3
batch = train_images[128 * n:128 * (n + 1)]

对于这种批量张量，第一个轴（轴0）叫作批量轴（batch axis）或批量维度（batch dimension）。在使用Keras和其他深度学习库时，你会经常遇到“批量轴”这个术语。

现实世界中的数据张量实例

我们来具体看看你以后会遇到的几个数据张量实例，你要处理的数据几乎总是属于下列类别：

向量数据：形状为(samples, features)的2阶张量，每个样本都是一个数值（“特征”）向量。

时间序列数据或序列数据：形状为(samples, timesteps,features)的3阶张量，每个样本都是特征向量组成的序列（序列长度为timesteps）。

图像数据：形状为(samples, height, width, channels)的4阶张量，每个样本都是一个二维像素网格，每个像素则由一个“通道”（channel）向量表示。

视频数据：形状为(samples, frames, height, width,channels)的5阶张量，每个样本都是由图像组成的序列（序列长度为frames）。

向量数据

这是最常见的一类数据。

对于这种数据集，每个数据点都被编码为一个向量，因此一个数据批量就被编码为一个2阶张量（由向量组成的数组），其中第1个轴是样本轴，第2个轴是特征轴（features axis）。

时间序列数据或序列数据

当时间（或序列顺序）对数据很重要时，应该将数据存储在带有时间轴的3阶张量中。

每个样本可被编码为一个向量序列（2阶张量），因此一个数据批量就被编码为一个3阶张量。

图像数据

 图像通常具有3个维度：高度、宽度和颜色深度。

虽然灰度图像（比如MNIST数字图像）只有一个颜色通道，因此可以保存在2阶张量中，但按照惯例，图像张量都是3阶张量。对于灰度图像，其颜色通道只有一维。因此，如果图像大小为256×256，那么由128张灰度图像组成的批量可以保存在一个形状为(128,256, 256, 1)的张量中，由128张彩色图像组成的批量则可以保存在一个形状为(128, 256, 256, 3)的张量中。

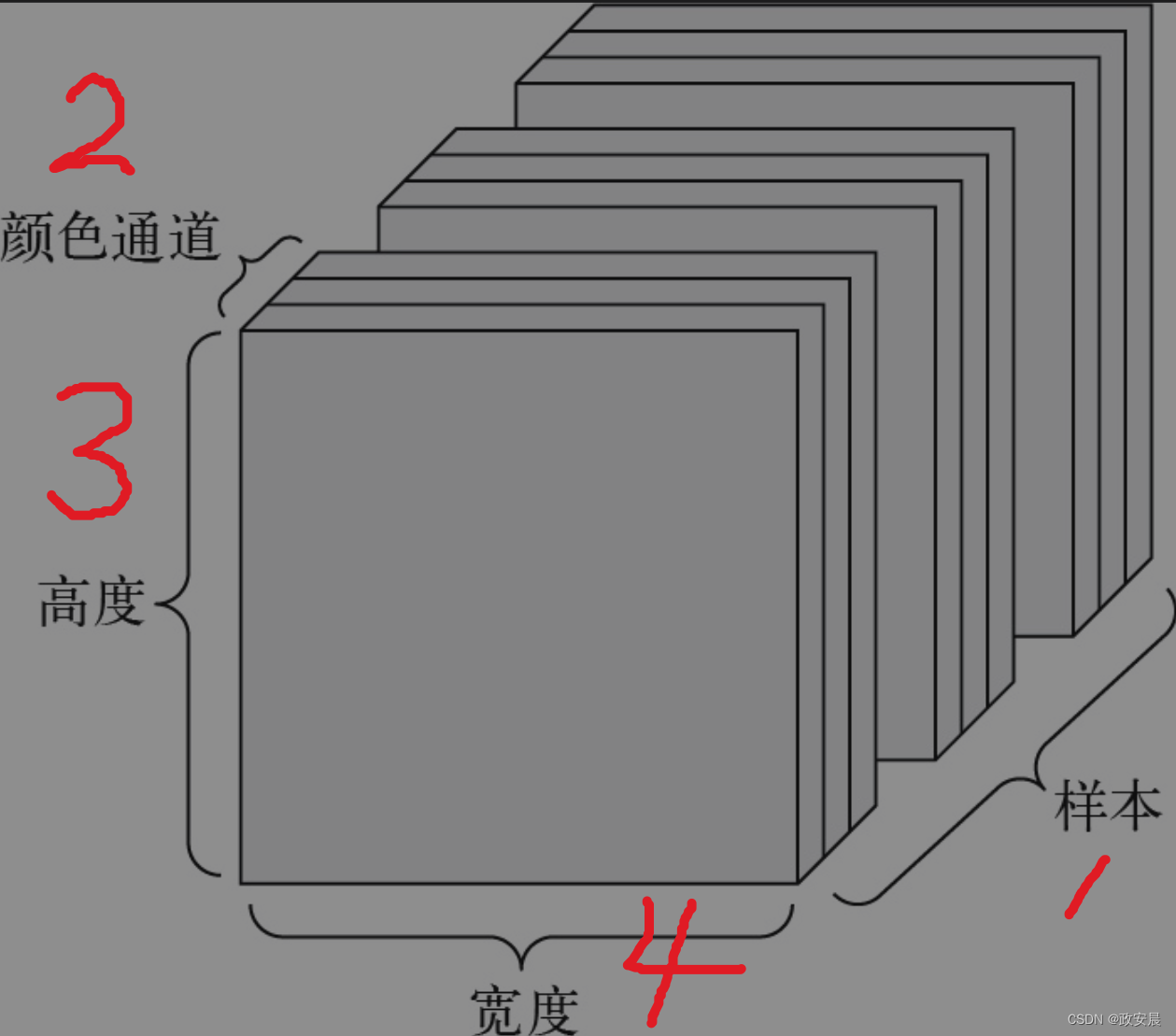
图像张量的形状有两种约定：通道在后（channels-last）的约定（这是TensorFlow的标准）和通道在前（channels-first）的约定（使用这种约定的人越来越少）。

通道在后的约定是将颜色深度轴放在最后：(samples, height, width,color_depth)。与此相对，通道在前的约定是将颜色深度轴放在紧跟批量轴之后：(samples, color_depth, height, width)。如果采用通道在前的约定，那么前面两个例子的形状将变成(128, 1, 256, 256)和(128, 3, 256,256)。Keras API同时支持这两种格式。

视频数据

视频数据是现实世界中为数不多的需要用到5阶张量的数据类型。视频可以看作帧的序列，每一帧都是一张彩色图像。由于每一帧都可以保存在一个形状为(height, width, color_depth)的3阶张量中，因此一个视频（帧的序列）可以保存在一个形状为(frames, height, width, color_depth)的4阶张量中，由多个视频组成的批量则可以保存在一个形状为(samples, frames,height, width, color_depth)的5阶张量中。

例如：

一个尺寸为144×256的60秒视频片段，以每秒4帧采样，那么这个视频共有240帧。

4个这样的视频片段组成的批量将保存在形状为(4, 240,144, 256, 3)的张量中。这个张量共包含106 168 320个值！如果张量的数据类型（dtype）是float32，每个值都是32位，那么这个张量共有405 MB。这样算来，这个文件确实不小！但是你在现实生活中遇到的视频要小得多，因为它们不以float32格式存储，而且通常被大大压缩（比如MPEG格式）。

---

（本篇将与下一篇一起将完成整个神经网络数学基础的核心概念演绎）