目录
位运算算法原理
①力扣191. 位1的个数
解析代码
②力扣338. 比特位计数
解析代码
③力扣461. 汉明距离
解析代码
位运算算法原理
常见位运算解题方法:
1. 基础位运算:
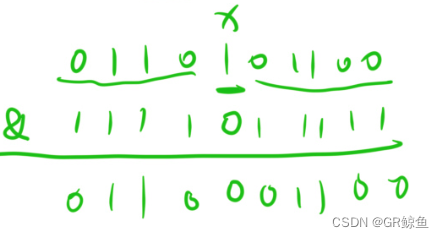
&:按位与,有0就是0
| :按位或,有1就是1
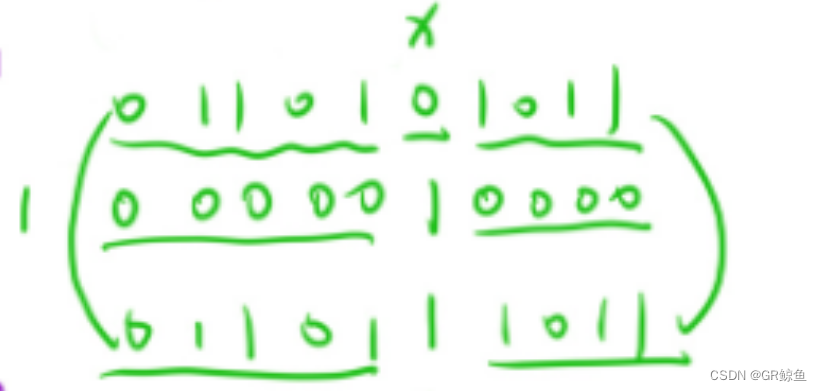
^ :按位异或,相同为0,相异为1/无进位相加
2. 给一个数 n,确定它的二进制表示中的第 x 位是 0 还是 1:
(n>>x)& 1 (n右移x位,按位与1)
为0则第x位为0,为1则第x位为1
3. 将一个数 n 的二进制表示的第 x 位修改成 1:
n l=(1<<x) (n或等 1左移x位)
4. 将一个数 n 的二进制表示的第 x 位修改成 0:
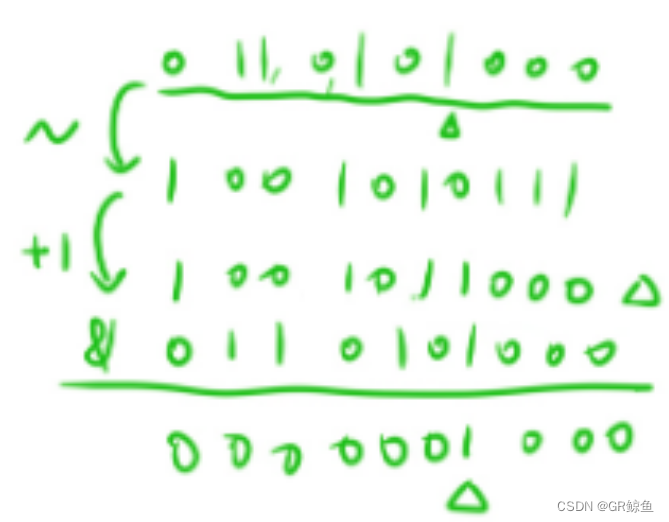
n&=(~(1<<x)) (n与等 1左移x位然后按位取反)
5. 提取一个数 n 二进制表示中最右侧的1:
n &-n(将最右侧的 1,左边的区域全部变成相反)
6. 干掉一个数 n 二进制表示中最右侧的 1(循环此方法知道n为0即可计算n二进制1的数目)
n & (n-1) (将最右侧的1,右边的区域(包含1)全部变成相反)
①力扣191. 位1的个数
191. 位1的个数
难度 简单
编写一个函数,输入是一个无符号整数(以二进制串的形式),返回其二进制表达式中数字位数为 '1' 的个数(也被称为汉明重量)。
提示:
- 请注意,在某些语言(如 Java)中,没有无符号整数类型。在这种情况下,输入和输出都将被指定为有符号整数类型,并且不应影响您的实现,因为无论整数是有符号的还是无符号的,其内部的二进制表示形式都是相同的。
- 在 Java 中,编译器使用二进制补码记法来表示有符号整数。因此,在 示例 3 中,输入表示有符号整数
-3。
示例 1:
输入:n = 00000000000000000000000000001011
输出:3
解释:输入的二进制串 00000000000000000000000000001011 中,共有三位为 '1'。
示例 2:
输入:n = 00000000000000000000000010000000 输出:1 解释:输入的二进制串 00000000000000000000000010000000 中,共有一位为 '1'。
示例 3:
输入:n = 11111111111111111111111111111101 输出:31 解释:输入的二进制串 11111111111111111111111111111101 中,共有 31 位为 '1'。
提示:
- 输入必须是长度为
32的 二进制串
进阶:
- 如果多次调用这个函数,你将如何优化你的算法?
class Solution {
public:int hammingWeight(uint32_t n) {}
};解析代码
看到上面的原理:
6. 干掉一个数 n 二进制表示中最右侧的 1(循环此方法知道n为0即可计算n二进制1的数目)
n & (n-1) (将最右侧的1,右边的区域(包含1)全部变成相反)
class Solution {
public:int hammingWeight(uint32_t n) {int cnt = 0;while(n){n &= (n - 1);++cnt;}return cnt;}
};②力扣338. 比特位计数
191. 位1的个数
给你一个整数 n ,对于 0 <= i <= n 中的每个 i ,计算其二进制表示中 1 的个数 ,返回一个长度为 n + 1 的数组 ans 作为答案。
示例 1:
输入:n = 2 输出:[0,1,1] 解释: 0 --> 0 1 --> 1 2 --> 10
示例 2:
输入:n = 5 输出:[0,1,1,2,1,2] 解释: 0 --> 0 1 --> 1 2 --> 10 3 --> 11 4 --> 100 5 --> 101
提示:
0 <= n <= 10^5
解析代码
只是(力扣191. 位1的个数)加了个循环:
class Solution {
public:vector<int> countBits(int n) {vector<int> v(n+1, 0);for(int i = 1; i <= n; ++i){int cnt = 0, tmp = i;while(tmp){tmp &= (tmp - 1);++cnt;}v[i] = cnt;}return v;}
};③力扣461. 汉明距离
461. 汉明距离
两个整数之间的 汉明距离 指的是这两个数字对应二进制位不同的位置的数目。
给你两个整数 x 和 y,计算并返回它们之间的汉明距离。
示例 1:
输入:x = 1, y = 4 输出:2 解释: 1 (0 0 0 1) 4 (0 1 0 0)↑ ↑ 上面的箭头指出了对应二进制位不同的位置。
示例 2:
输入:x = 3, y = 1 输出:1
提示:
0 <= x, y <= 2^31 - 1
解析代码
把两个数异或起来,计算其结果二进制1的数目:
class Solution {
public:int hammingDistance(int x, int y) {// return __builtin_popcount(x ^ y);int tmp = x ^ y, cnt = 0; // 不同则为1while (tmp) {tmp &= (tmp - 1);++cnt; // 依次左移到最低位}return cnt;}
};