个人主页:PingdiGuo_guo
收录专栏:C++干货专栏

铁汁们新年好呀,今天我们来了解自定义函数。
文章目录
1.数学中的函数
2.什么是自定义函数
3.自定义函数如何使用?
4.值传递和引用传递(形参和实参区分)
1.值传递
2. 引用传递
3. 形参与实参的区别
5.自定义递归函数
6.嵌套调用和链式调用
1.链式调用
2.嵌套调用
7.自定义函数和库函数的对比
8.自定义函数的练习
9.总结
1.数学中的函数
在数学中,函数是一种基本的数学对象,它建立了一个集合(称为定义域)中的每个元素与另一个集合(称为值域)中的唯一元素之间的对应关系。简单地说,函数就是一个规则,它接收一个或多个输入值(也称为自变量),并据此产生一个确定的输出值(称为函数值或因变量)。
数学上的函数通常用 ( f ) 表示,并写作 ( y = f(x) ),这里的 ( x ) 是自变量,( y ) 是相应于 ( x ) 的函数值。例如,线性函数 ( f(x) = mx + b ) 就是一条直线的方程,其中 ( m ) 是斜率,( b ) 是截域。

2.什么是自定义函数
自定义函数是在C++或其他编程语言中由程序员自行创建的函数,用于封装一组操作或计算逻辑,以便在多个地方重复使用或者模块化代码。自定义函数允许开发者按照自己的需求来定制功能,并且可以根据程序的具体情况调整其行为。
3.自定义函数如何使用?
1. 声明函数原型:
在函数体之前(通常在头文件或源文件的开始部分),你需要声明函数,包括返回类型、函数名以及参数列表(如果有的话):
// 声明一个自定义函数原型
double calculateArea(double radius);
这个例子声明了一个名为calculateArea的函数,它接受一个double类型的参数(半径),并返回一个double类型的值(面积)。
2. 定义函数体:
在函数声明之后,你需要定义函数的实际实现,即写出完成特定任务的代码块:
// 定义函数体
double calculateArea(double radius) {
double area = 3.14159 * radius * radius;
return area;
}
3. 调用函数:
在程序的适当位置,你可以像使用库函数一样调用自定义函数:
int main() {
double myRadius = 5.0;
double result = calculateArea(myRadius);
cout << "The area of the circle with radius " << myRadius << " is: " << result << endl;
return 0;
}4.值传递和引用传递(形参和实参区分)
1.值传递
- 当函数通过值传递方式接收参数时,它会创建实参的副本(复制一份实参的值)并将这个副本传递给函数内部的形参。
- 形参的变化不会影响实参,因为两者存储在不同的内存位置。
- 值传递通常适用于不需要修改实参值的情况。
示例:
void swapByValue(int a, int b) {
int temp = a;
a = b;
b = temp;
}
int main() {
int x = 10, y = 20;
swapByValue(x, y); // 调用函数后,x和y的值不变,因为交换的是函数内部形参的值
}
2. 引用传递
- 引用传递是将实参的引用(也就是实参的别名)传递给函数的形参,这样形参就直接指向实参的内存地址。
- 如果在函数内部改变了引用类型的形参,那么相应地,实参的值也会被修改。
- 引用传递常用于需要更改实参或避免大型数据结构复制的成本时。
示例:
void swapByReference(int& a, int& b) {
int temp = a;
a = b;
b = temp;
}
int main() {
int x = 10, y = 20;
swapByReference(x, y); // 调用函数后,x和y的值会互换,因为函数内部修改的是实参的内存
}
3. 形参与实参的区别
- 实参(Actual Parameter):在函数调用过程中,传递给函数的实际值。例如上面例子中的 x和 y 就是实参。
- 形参(Formal Parameter):在函数定义中,用来接收传递进来的值的变量。如上述例子中的 a 和 b 是形参,它们在函数内部代表了从外部传入的值。
总结来说,在函数调用过程中,实参是实际提供的值,而形参是函数声明中用来接收这些值的地方。在C++中,值传递和引用传递决定了函数操作的是实参的副本还是实参本身。
5.自定义递归函数
递归调用函数是在函数内部调用自身的一种编程技术。这种技术在解决具有自我重复性质的问题时非常有用,如树的遍历、动态规划中的某些子问题解法、分治算法中的问题拆解等。
递归函数通常包含两个基本部分:
- 基本情况(Base Case):这是递归结束的条件,即当达到某个特定条件时,不再进行下一层递归调用,而是直接返回一个确定的结果。
- 递归步骤(Recursive Step):在此阶段,函数通过调用自身来解决规模更小的相同问题,直到满足基本情况为止。
下面是一个简单的递归函数示例,计算阶乘(Factorial):
#include <iostream>// 递归函数实现阶乘
int factorial(int n) {
// 基本情况:0的阶乘为1
if (n == 0)
return 1;
// 递归步骤:n的阶乘等于n乘以(n-1)的阶乘
else
return n * factorial(n - 1);
}int main() {
int num = 5;
std::cout << "The factorial of " << num << " is: " << factorial(num) << std::endl;
return 0;
}
在这个例子中,factorial 函数在每次递归调用时都会将问题规模缩小(减少参数n的值),直到遇到基本情况n为0时停止递归,然后逐层返回计算结果。
6.嵌套调用和链式调用
1.链式调用
链式调用是一种编程风格,可以在调用多个方法时使用点操作符将它们连接在一起,形成一个链。在每个方法调用后,都会返回一个对象,可以继续调用其他方法。这样就可以在一行代码中实现多个方法的调用,使代码更加简洁和可读性更高。
步骤一:定义一个支持链式访问的类
class Chainable {
public:
// 构造函数
Chainable(int initial_value) : value(initial_value) {}// 第一个链式方法(假设增加值)
Chainable& increment(int step = 1) {
value += step;
return *this; // 返回当前对象的引用以支持链式调用
}// 第二个链式方法(假设加倍)
Chainable& doubleValue() {
value *= 2;
return *this;
}
private:
int value;
};
步骤二:创建对象并开始链式调用
int main() {
// 创建Chainable对象
Chainable obj(5);// 链式访问与调用
obj.increment(3).doubleValue();// 这里原本可能还有其他方法继续调用...
// ...// 最终可以验证对象的值
std::cout << "Final value: " << obj.value << std::endl;return 0;
}
在上述代码中,首先定义了一个名为Chainable的类,它有两个链式方法:increment()和doubleValue()。这两个方法都在执行相应的操作之后返回了对当前对象的引用,使得可以连续调用这些方法,形成链式调用。在main()函数中展示了如何使用这种方式连续调用两个方法来处理同一个对象。
2.嵌套调用
嵌套调用是指在一个方法内部调用另一个方法,并且被调用的方法又可以继续调用其他方法,形成多层嵌套的调用关系。嵌套调用可以在程序中实现复杂的逻辑和功能,将代码进行模块化和组合,提高代码的可复用性和可维护性。
在嵌套调用中,每个方法的返回值可以作为下一个方法的参数,这样可以将多个方法串联起来,实现一系列的操作。嵌套调用的层级可以根据具体需求进行设计,可以是两层、三层,甚至更多。
步骤1:定义一个包含内部函数的外部函数:
void outerFunction(int x) {
// ...
void innerFunction();
// ...
}
步骤2:定义内部函数的具体实现:
void outerFunction(int x) {
std::cout << "In outer function with x = " << x << std::endl;void innerFunction() {
std::cout << "In inner function." << std::endl;
}
}
步骤3:在外部函数内部调用内部函数:
void outerFunction(int x) {
// ...
innerFunction(); // 这里是嵌套调用发生的地方
// ...
}
步骤4:完整外部函数及其调用示例:
void outerFunction(int x) {
std::cout << "In outer function with x = " << x << std::endl;void innerFunction() {
std::cout << "In inner function." << std::endl;
}innerFunction();std::cout << "Continuing in outer function after inner call." << std::endl;
}int main() {
outerFunction(5); // 在主函数中调用outerFunction
return 0;
}
输出:
In outer function with x = 5
In inner function.
Continuing in outer function after inner call.7.自定义函数和库函数的对比
- 自定义函数:
- 由程序员根据具体需求编写。
- 可以自由命名,具有高度灵活性。
- 具体实现完全取决于程序员,可修改、优化或扩展。
- 只能在包含它们的源文件或链接到它们的库中调用。
- 库函数:
- 预先编写好的、经过充分测试的标准函数,通常由语言本身或第三方库提供。
- 名称和功能通常是标准化的,如C++标准库中的std::sort()、std::cos()等。
- 不需要程序员重新实现,只需包含适当的头文件并在程序中正确调用即可。
- 通常跨平台兼容性更好,因为它们遵循语言规范和标准。
- 提供的功能广泛多样,涵盖基础数据结构操作、数学计算、输入/输出处理等多个方面。
总结来说,自定义函数的核心价值在于它可以针对性地解决特定的问题,并且有助于提高代码的复用性和组织性;而库函数则是为了提供通用的、高效的功能组件,减少重复劳动,提升开发效率和程序质量。
8.自定义函数的练习
假设我们要编写一个C++函数,它接受两个整数作为参数,返回它们的最大公约数(Greatest Common Divisor, GCD)。这个功能可以通过使用欧几里得算法(Euclidean algorithm)来实现。下面是这个函数的定义和使用示例:
#include <iostream>// 自定义函数:计算两个整数的最大公约数
int gcd(int a, int b) {
// 边界条件:如果b为0,则a就是最大公约数
if (b == 0)
return a;// 否则,递归地计算(a mod b)和b的最大公约数
return gcd(b, a % b);
}int main() {
int num1 ,num2 ;
std::cin>>num1>>num2;// 调用自定义函数并输出结果
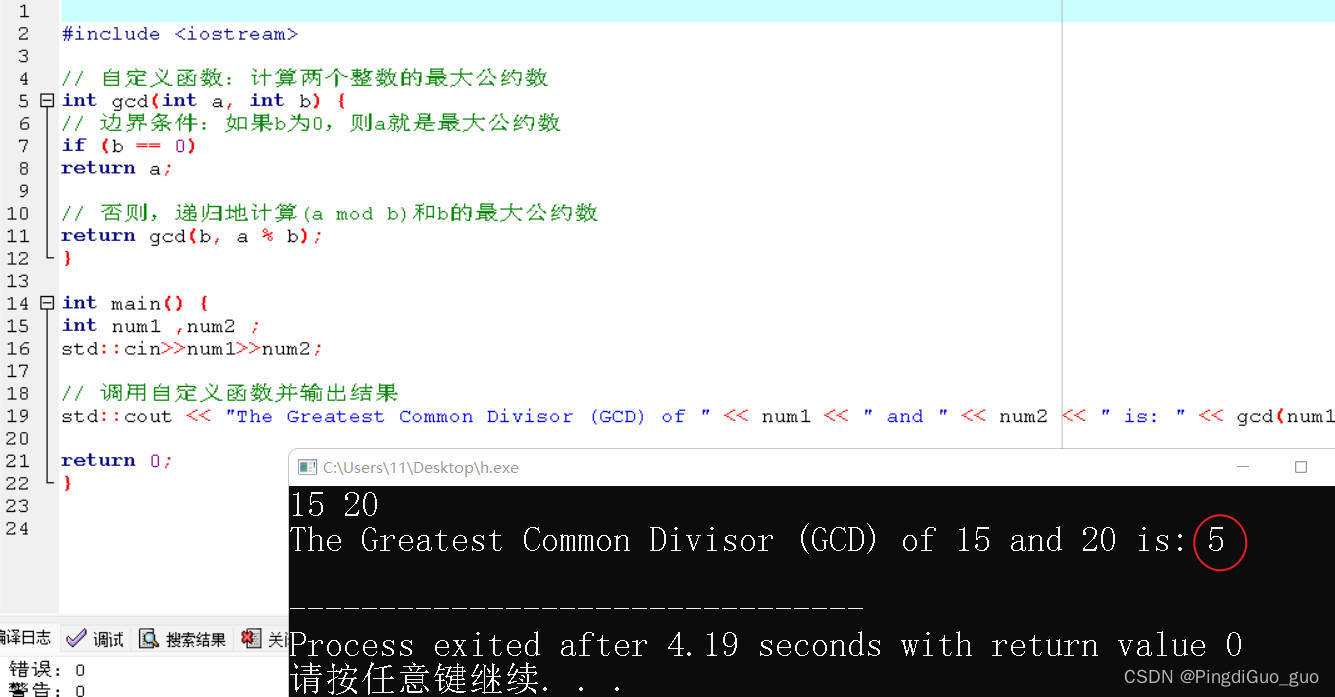
std::cout << "The Greatest Common Divisor (GCD) of " << num1 << " and " << num2 << " is: " << gcd(num1, num2) << std::endl;return 0;
}
上述代码首先定义了一个名为gcd的函数,该函数采用两个整数作为参数,并使用递归方法找到它们的最大公约数。在main函数中,我们创建了两个变量并调用了gcd函数来计算它们的最大公约数,最后将结果输出到控制台。
9.总结
本篇博客到这里就结束了,感谢大家的支持与观看,如果有好的建议欢迎留言,谢谢大家啦!


![[BUUTF]-PWN:wdb2018_guess解析](https://img-blog.csdnimg.cn/direct/1de90b7b31d84e238d684ffe51f7e131.png)