文章目录
- 概率论的基本概念
- 放杯子问题
- 条件概率与重要公式的结合
- 独立的运用
- 随机变量以及分布
- 离散随机变量的分布函数特点
- 连续随机变量的分布函数在某一点的值为0
- 正态分布标准化
- 随机变量函数的分布
- 多维随机变量以及分布
- 条件概率
- max 与 min 函数的相关计算
- 二维随机变量
- 二维随机变量求边缘概率密度
- 独立性
- Z = X + Y
- max{X,Y}
- 离散二维随机变量的条件概率以及max 与min
- 随机变量的数字特征
概率论的基本概念
- 1.互斥事件(互不相容)与对立事件:A 与 B 的交集为空集,A 和 B 不可能同时发生,区别于对立事件(在互斥事件的基础上,A 和 B 的和为全集)
- 对于互斥事件有 P(A + B + C ··· + Z) = P(A) + P(B) + P( C) + ··· + P(Z)
- 对于一般的不是互斥,
P(A+B) = P(A) + P(B ) - P(AB)这里不是P(A)*P(B),三个变量
P(A+B+C) = P(A) + P(B) + P© -P(AB) -P(AC) -P(BC) +P(ABC)- 古典概型,条件概率,三个重要的公式:乘法公式,全概率公式(化整为零),贝叶斯公式(利用先验概率求后验概率)
- 事件的独立性:P(AB) = P(A)P(B) ,三个事件的独立性要有四个式子成立------> n 各事件相互独立,则任意的2到n-1 的事件都相互独立,替换成对立事件也是成立的
- P(AB) = P(A) - P(AB非) 这个式子通过包含关系直接推出

为什么分母不使用12*11*10 ,分析,使用这个的话要注意 ,其实这个是A(3,10),那么就是讲究顺序的了,由于筛选是最终的结果,是不讲究顺序的,只能用C(3,10)
放杯子问题
- 将三个小球放进4各杯子,问杯中的最大小球个数分别为1,2,3的概率
站在小球的角度,选择杯子
- 对于1:那么就是432 / 444
- 对于3 :就是C(1,4) / 444
- 对于2: 就是1 - P(1) - P(3)
条件概率与重要公式的结合


可能一开始对于 求P(A2) 没有什么思路,搞不清楚应该怎么算,这时可以考虑用全概率公式

独立的运用

随机变量以及分布
- 注意区分离散型随机变量:二项分布,(0-1)分布,泊松分布,注意对它们分布列以及分布函数的求解(端点值?)
- 连续随机变量:均匀分布,指数分布,正态分布
- 指数分布是没有记忆性的P{X>s+t|X>s} = P{X>t}
- 二项分布的趋近为(np)泊松分布和正态分布
- 正态分布在u= 0 ,方差为1 时称为标准的正态分布

离散随机变量的分布函数特点


注意离散型随机变量的分布律与分布函数的关系
连续随机变量的分布函数在某一点的值为0

正态分布标准化

注意对带有绝对值的转换,以及带有负数的转换
随机变量函数的分布



对于函数是单调的话,可以使用公式法快速求解,如果不是单调的话,就按照定义一步步求解注意开始计算的时候,要提前确定好,Y 的范围,是否直接大于0,还是什么范围
多维随机变量以及分布
- 边缘分布:其中 Z = X + Y ,所得到的z 的边缘分布被称为卷积公式
- 对于 M =max{X,Y} 与 N = min{X,Y} 的分布函数的求法,其中X,Y 相互独立,且各自的分布函数Fx(x) 与 Fy(y) 那么有 F max(z) = Fx(x) * Fy(y) Fmin(z) = 1- (1-Fx(x))*(1-Fy(y))
对于上面的情况可以推广到 n 各相互独立的随机变量 ,都可以成立
最主要的是要分清,到底式子的形式是概率密度还是分布函数
条件概率

max 与 min 函数的相关计算

0.84 0.16
二维随机变量
对于开始的未知数的求解:分布函数的整体为1(1)对于X,Y 的确切的值的,就在相对应的面积范围内求解(2)对于边缘分布的,一方为给出的范围,另一方则为全部范围(3)像下面的第四题,其实的真正的目的,就是给x,y 一个更加具体的一个范围进行求解
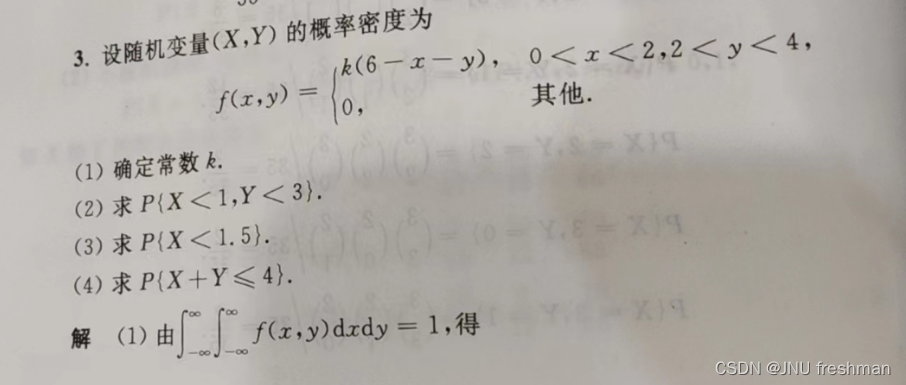

二维随机变量求边缘概率密度
以下面的第二问为例子:当你求x 的边缘概率密度时,你要把x 当作一个已经已知范围的一个常量,实际上y 才是你的变量,这就好比你其实是在求一条线(每当x 确定的时候),所以在求积分的上下限的时候,这时得到的应该是变量y 关于 x 的范围 , 也就是[x^2 , 1] ,当你求y 的概率密度的时候,y 就变成了常量,积分的上下限应该是变量x 关于常量 y 的一个范围,也就是[ - 根号 y, 根号y ]

独立性
对于独立性的证明,就按照定义来即可,分布函数或者概率密度都可以


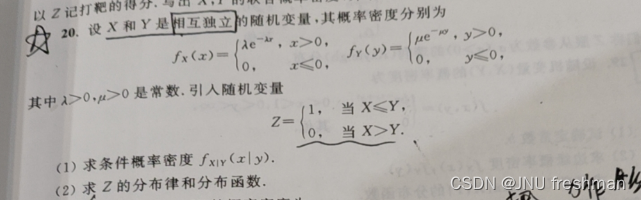

简单的分析:由一开始的独立性,得出f(x,y),对于后面的z ,其实 z 的取值范围已经给出,所谓的求分布律就是让你求相对应的概率,这个概率也就是f(x,y) 相对应的概率
Z = X + Y
卷积的两种方法都是等价的,不过下面的第一种方法相对来说更加简单,计算以及运算的过程在于你的选择利用公式来求,同样地,与求边缘概率密度一样,这里将z 看成常量,x 和 y 是看成以 z 为变量的一个函数,有时候是要进行分段进行一个计算并不建议一个大括号直接运算完成,而是以z 的范围作为分隔,一个个进行计算
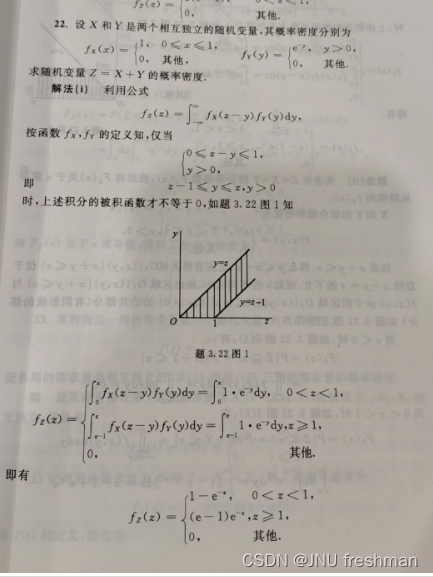
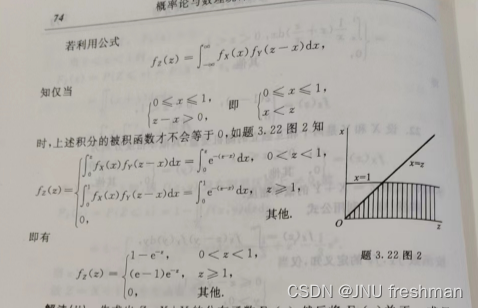
max{X,Y}
注意最后的时候的变量都替换成u 了

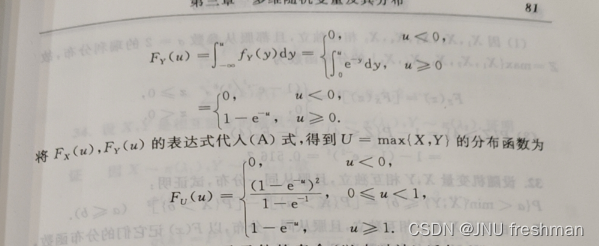
离散二维随机变量的条件概率以及max 与min
在离散随机变量中,条件概率的理解 p{X = 2| Y = 2} 由于是在Y = 2 的条件下,那么就要将Y = 2 的全部情况算进去(不止一个x) ,但是X = 2 的话,就只是一个x ,同理是可以类推到连续的随机变量的
对于离散型的max 与min 的话,不如直接列举进行一个计算,连续型才用公式
随机变量的数字特征
- (1) 懂得离散型随机变量与连续型随机变量的期望的求法
- (2)随机变量的函数的数学期望:对于离散型,直接将每个取值代入函数,得到新的取值,再和相对应的概率相乘再相加即可;对于连续型随机变量,直接对g(x)f(x) 进行积分 ,(区别于f(x) 自身的期望, xf(x) 的积分
- (3)对于二维的随机变量:对于离散型,就是相对应的取值乘概率后相加;对于连续型就变成 对g(x,y)f(x,y) 的一个求积分的过程
- (4) 注意期望的相关计算的公式:E(x+y) = E(x) + E(y) (减号也是一样) E(XY) = E(X)E(Y) 当X,Y 相互独立的时候成立 (这两个公式均可以推广)
- (5)方差 D(x) = E{[X-E(X)]^2} ,就是每一个取值与期望的差的平方的期望,它的算数平方根为均方差
当计算离散随机变量的时候,[X-E(X)]^2 乘相对应的概率再求和即可; 连续型的时候 [X-E(X)] ^2 乘f(x) 的积分由于计算方差难度问题,常常用 D(X) = E(X^2) - [E(X)]^2 来计算- 方差的相关性质:常数的方差为0, D(cX) = c^2 D(X) D(C+ X) = D(X)
D(X+Y ) = D(X) + D(Y) + 2E{(X-E(x))(Y-E(y))}
D(X-Y ) = D(X) + D(Y) - 2E{(X-E(x))(Y-E(y))}
当X ,Y 相互独立的时候,D(X+Y) = D(X-Y) = D(X) + D(Y)- 标准化的随机变量,就是 X- E(X) / 均方差
- 协方差 Cov(X,Y) = E{(X-E(x))(Y-E(y))} 相关系数 = Cov(X,Y) /X 的均方差乘Y的均方差
- 协方差可以写成 Cov(X,Y) = E(XY) - E(X)E(Y)
- 协方差的相关性质 Cov(aX,bY) = abCov(X,Y) Cov(X1+X2,Y) = Cov(X1,Y) + Cov(X2+Y)
相关系数 = 0 时,称为X 与 Y 不相关(就是X 与 Y 没有线性关系,但是可能会存在其他的关系)相互独立可以推出不相关,但是不相关推不出相互独立, 不相关 与 相关系数 = 0,Cov(X,Y) =0 E(XY) = E(X)E(Y)对于二维正态随机变量的相互独立与不相关的条件是相互等价的
- 矩、协方差矩:分清k 阶原点矩,k 阶中心距,k+l 阶混合矩 k + l 阶混合中心矩

切比雪夫不等式给出了再随机变量X 的分布未知,只知道E(X) 与D(X) 的情况下,对E{|X-E(X)|<=m} 概率的下限的估计