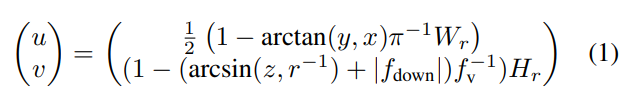目录
暴力做法
代码如下
KMP算法
不同的next求法-----视频讲解/博客推荐
视频推荐
博客推荐
课本上的方法-
prefix的方法-
求next数组思路---next数组存放前缀表的方式
s和p匹配思路
代码如下

暴力做法
遍历s主串中每一个元素,如果该元素等于模板串p中的第一个元素,就进入内层遍历模板串p中的每一个字符,看该元素及其后面几个元素是否都与模式串p完全一致。避免起初 i 下标丢失,需要定义几个变量,代替 i 作为下标索引。如果发现有不同的,说明这个起始元素并不是我们想要的答案,执行内层循环的if语句,start是我们判断的标记,如果执行了if语句start赋值为-1,说明不必将原本的start放进答案数组。
由此得出答案。
需要注意定义ans答案数组为vector动态数组,其添加元素直接调用push_back()函数。(问就是我刚开始写错了[点手指]...)
代码如下
#include<iostream>
#include<vector>
using namespace std;
int main()
{int n,m;string p,s;cin>>n;cin>>p;//模板串 子串cin>>m;cin>>s;//模式串 主串int k=0;int start=-1;vector<int> ans;int v=0;for(int i=0;i<m;i++){if(s[i]==p[0]){start=i;k=start;for(int j=0;j<n;j++,k++){if(s[k]!=p[j]){k=0;start=-1;break;}}if(start!=-1)ans.push_back(start);}}for(int i=0;i<ans.size();i++){cout<<ans[i]<<" ";}return 0;
}KMP算法
就像是在归并排序过程中顺便计算出了逆序对一样,我们在暴力做法里,每次匹配的过程中也做了一些后期优化能够利用上的过程
kmp算法思想:用来求解模式串匹配的相关问题。每次我们s主串数组和p模式串数组进行匹配的过程中,已经有一部分是匹配的,而发现下一个元素不匹配,此时我们如果存在next数组记录着p模式串中每个元素之前的前缀和后缀的最长相等的长度,就可以让p数组移动到与其后缀对齐的位置,继续向下比较 (这个"移动"是通过更新索引j来改变我们接下来要比较的元素,而不是实际改变模式串p的位置),从而提高了效率.
不同的next求法-----视频讲解/博客推荐
在写完这个思路之后,我发现这里我们这种方法求得的next数组其实和课本上,如下图

这种方法所得的结果是不一致的。
视频推荐
b站这个姐姐按课本上的计算方法讲的很清晰,放在这里啦,放心食用~(提一下这个姐姐也讲了数据结构重点知识的速成课,讲的也很不错,最近要期末考的[我]可以看看~)
http:www.bilibili.com/video/BV1PG4y1V7Zq?vd_source=02dfd57080e8f31bc9c4a323c13dd49c
其实这种next数组的求法是 我们这里使用的前缀表得出的next数组统一向右移一位,第一位补-1,再同时给每个数+1所得到的。(我把我们使用得前缀表的方法用prefix来表示)

下面这个视频中有一些动态的匹配过程,可以看看帮助理解一下思路~
http:www.bilibili.com/video/BV1jb411V78H?vd_source=02dfd57080e8f31bc9c4a323c13dd49c
这里我真困惑了好一阵,又看了很多其他的视频讲解,下面是b站代码随想录老师按照我们这里next数组存前缀表的理论方法讲解的很详细👇可以多看几遍
http:www.bilibili.com/video/BV1PD4y1o7nd?vd_source=02dfd57080e8f31bc9c4a323c13dd49c
同时老师也出了专门讲代码的视频,那个视频前5分钟讲的是next的不同实现方法,解决了我关于这方面的疑惑,可以看一下哦~
博客推荐
也看了一些博客,不过感觉视频讲解更清楚明了一些,视频讲解优先~(这些博客我没有完整的看完[比较长] 只是一股优质好文的味道)
课本上的方法-
这个是给出了动态图片,比较好理解
http://blog.csdn.net/qq_37969433/article/details/82947411
这个是对课本上next数组的定义进行了详细的阐释
http://blog.csdn.net/weixin_46307478/article/details/124589160
prefix的方法-
这两篇是和本篇我写的方法一致,感觉讲的更清晰一些[惭愧] 一起学习
http://blog.csdn.net/qq_52127701/article/details/126057058
http://zhuanlan.zhihu.com/p/576363046?utm_id=0
这个对跳转的过程(即j指针的移动)展示的比较清晰
http://blog.csdn.net/weixin_43972154/article/details/121357012
这个是详细解释了优化的地方
http://blog.csdn.net/oceanriverguo/article/details/129644605
求next数组思路---next数组存放前缀表的方式

我们手算的方法就像图里这样。下面是对应代码,感觉不太好理解。
for(int i=2,j=0;i<=n;i++){while(j && p[i]!=p[j+1])j=ne[j];if(p[i]==p[j+1])j++;ne[i]=j;}对于模式串p的每一个位置 i,我们都试图找出其最长的相等前后缀的长度,也就是ne[i],即ne[i] 表示模式串 p 的前缀 p[1,i ] 的最长相等前缀和后缀的长度。
i 表示当前正在考虑的模式串字符的位置。遍历p数组每一个元素,找出其对应的ne[j]
j 表示当前已匹配过的模式串的最长前缀和后缀相等的长度.默认是前缀 j 个元素。
如果p[i] (模式串的第 i 个字符)与前缀的下一个字符 p[ j+1] 相等,我们增加 j 的值,表示找到了更长的相等前缀和后缀。
while循环的作用:通过不断缩短 j 的值,寻找当前位置 i 对应的字符的最长前缀和后缀相等的长度
我们需要执行 while 循环,因为在 p[i] != p[j+1] 的情况下,我们希望继续缩短 j,直到找到满足 p[i] == p[j+1] 的 j。通过这个过程,我们能够确保在当前位置 i 找到的 j 是满足条件的最大值。
while循环条件: j && p[i]!=p[j+1] ,当 j 为零时,表示当前没有已匹配的前缀和后缀相等的部分,就不需要缩短j 。如果当前i所对元素与p[j+1]元素不等,说明不匹配。当发现不匹配时,我们希望缩短 j。ne[j] 存储了当前前缀 p[1..j] 的最长相等前缀和后缀的长度。所以,j = ne[j] 实际上将 j 缩短到前缀的最长相等前缀和后缀的长度,以便继续尝试寻找更短的相等部分。举例:
abcaabb 对应 Next数组:0 0 0 1 1 2 0
abcabcd 对应 Next数组:0 0 0 1 2 3 0
aabbacddc 对应 Next数组: 0 1 0 0 1 0 0 0 0
if(p[i] == p[j+1]) j++; 是在找到相等部分时增加 j 的值。且这个 j 的值在下一轮循环中会利用之前得到的 j。所以比如下面这个:我找第一个a的时候是0 第二个b也是0 ,第三个p[3]=p[1] 得到j=1;第四个,这是j已经不是等于1了,我们判断p[i]与p[j+1]的关系,这里是相等的,执行了该if语句,j++,此时j=2了。后面我只要看p[i]与p[j+1]相等的话我直接j+1,不等的话就和前面的数的ne[j]一致。这样计算很快了。

s和p匹配思路

上面next数组思路明白之后,这个匹配的过程思路是差不多了。
if(j==n){printf("%d ",i-n);j=ne[j];}这里我们遍历完之后,还是将j移动到ne[j]的位置,继续进行下一轮的匹配。
代码如下
#include<iostream>
using namespace std;
const int N=1e5+10,M=1e6+10;
int n,m;
char p[N],s[M];
int ne[N];//ne[1]=0
int main()
{cin>>n>>p+1>>m>>s+1;//因为我们希望从1开始存储元素,而默认下标从0开始 所以要+1//计算ne数组for(int i=2,j=0;i<=n;i++)//ne[1]=0{while(j && p[i]!=p[j+1])j=ne[j];if(p[i]==p[j+1])j++;ne[i]=j;}for(int i=1,j=0;i<=m;i++){while(j && s[i]!=p[j+1])j=ne[j];if(s[i]==p[j+1])j++;if(j==n){printf("%d ",i-n);//本来是i-n+1,但这里题目要求我们下标从0开始j=ne[j];}}return 0;
}kmp拖了好久了,感觉不太好理解,,, ,,写的不好,一些细节没有讲到(但推荐的文章里对这些部分讲的很清楚),懒了qaq,这几天状态不好。。。。
如果有问题欢迎指出,非常感谢!!
也欢迎交流和建议哦!