0. 简介
学习无人监督的自动驾驶世界模型有可能显著提高当今系统的推理能力。然而,大多数工作忽略了世界的物理属性,只关注传感器数据。提出MUVO,一个具有几何体素表示的多模态世界模型。用原始相机和激光雷达数据来学习传感器不可知的世界几何表示,可以直接用于下游任务,如规划。在多模态的未来预测,几何表示改进了相机图像和激光雷达点云的预测质量。代码可以在Github上获取。

图1. 这个例子展示了MUVO对3D占据和摄像头以及激光雷达观测的高分辨率未来预测
1. 主要贡献
我们利用自动驾驶车队收集的大量未标记传感器数据。我们的世界模型以原始的高分辨率摄像头图像和激光雷达点云作为输入,并根据行动预测多模态未来观测。为了使我们的模型具有更深刻的环境理解,我们还学习了一种与传感器无关的世界的三维几何表示。
我们的贡献可以总结如下:
• 一种利用自动驾驶车辆多模态传感器设置的新颖的无监督生成世界模型,并对摄像头和激光雷达的未来预测进行预测。
• 一种学习传感器无关的可操作环境表示的新方法,以三维几何体素占用表示的形式呈现世界模型。
• 一种行动条件下的三维占用预测的新方法,拓展了现有技术水平。
2. 方法
在这项工作中,我们提出了MUVO,一种具有几何体素表示的多模态世界模型。我们的模型利用自动驾驶车辆的高分辨率图像和激光雷达传感器数据,以预测原始相机和激光雷达数据,以及在多个步骤中基于动作条件的3D占据表示。
我们的模型包括三个阶段,如图2所示。首先,我们使用基于transformer的架构处理、编码和融合高分辨率RGB相机数据和激光雷达点云。其次,我们将传感器数据的潜在表示馈送到转换模型,以推导当前状态的概率模型,随后进行采样,同时预测未来状态的概率模型并从中进行采样。最后,我们从概率模型中解码当前和未来状态,预测原始RGB图像、点云和多帧未来的3D占据网格。
我们认为先前的世界模型主要学习数据中的模式,而不是对真实世界进行建模。我们的无监督学习传感器无关的几何占据表示的方法为模型提供了对物理世界的基本理解。
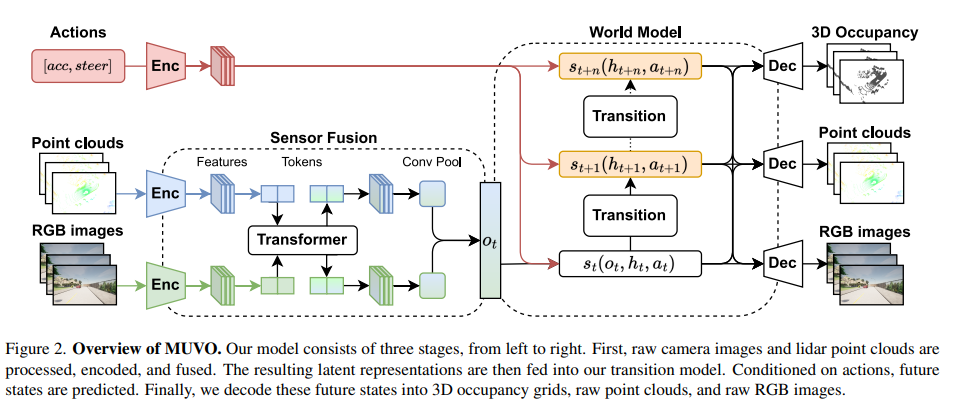
图2. MUVO概述。我们的模型由三个阶段组成,从左到右依次为:首先,对原始摄像头图像和激光雷达点云进行处理、编码和融合。然后,将得到的潜在表示输入到我们的转换模型中。在给定动作的条件下,预测未来状态。最后,将这些未来状态解码为3D占据网格、原始点云和原始RGB图像。
3. 观测编码器
3.1 输入表示
先前的多模态世界模型[90, 112]基于低分辨率输入,无法捕捉驾驶场景中的相关细节[15, 40]。相反,我们的模型建立在自动驾驶车辆典型传感器设置的基础上,包括立体摄像头和激光雷达[27, 109]。我们利用来自前置摄像头的RGB图像和来自顶部安装的激光雷达的点云作为网络的输入。对于多模态世界建模任务,我们发现激光雷达点云的双射、无损范围视图表示最为有效。此外,与基于体素的方法[24]相比,它们显示出计算上的优势。包括高达60,000个带有坐标 ( x , y , z ) (x, y, z) (x,y,z)的3D点云被投影到具有尺寸 H r × W r H_r × W_r Hr×Wr的2D圆柱形投影 R ( u , v ) R(u, v) R(u,v)中:
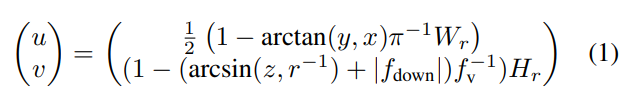
在2D范围视图图像中, ( u , v ) (u, v) (u,v)表示每个点的坐标。每个投影点的坐标 ( x , y , z ) (x, y, z) (x,y,z)和范围 r r r沿着维度轴堆叠形成 ( x , y , z , r ) (x, y, z, r) (x,y,z,r),作为2D范围视图图像中每个投影点的特征,导致 R ( u , v ) ∈ R 4 × H × W R(u, v) ∈ \mathbb{R}^{4×H×W} R(u,v)∈R4×H×W。对于没有投影点的像素,坐标 ( x , y , z ) (x, y, z) (x,y,z)设为 0 0 0, r r r被赋值为 − 1 -1 −1,有效地表示这些坐标处没有数据。对于图像 I ∈ R 3 × H i × W i I ∈ \mathbb{R}^{3×H_i×W_i} I∈R3×Hi×Wi,我们采用胡等人的建议[40]。我们的模型以分辨率为600×960像素的图像作为输入。随后,我们进行轻微裁剪以排除无关的区域,如天空。
3.2 编码器
对于图像数据 I ∈ R 3 × H i × W i I ∈ \mathbb{R}^{3×H_i×W_i} I∈R3×Hi×Wi和范围视图表示中的点云数据 R ∈ R 4 × H r × W r R ∈ \mathbb{R}^{4×H_r×W_r} R∈R4×Hr×Wr,我们利用预训练的ResNet-18 [36]作为特征提取的骨干。我们从不同的ResNet层中派生出多个特征图,分辨率较低,类似于[40]。然后,利用卷积层结合上采样或下采样技术融合这些特征图,最终得到图像特征 F c ∈ R C × H c × W c F_c ∈ \mathbb{R}^{C×H_c×W_c} Fc∈RC×Hc×Wc和点云特征 F L ∈ R C × H L × W L F_L ∈ \mathbb{R}^{C×H_L×W_L} FL∈RC×HL×WL。然后,这些编码表示被馈送到传感器融合组件。
4. 多模态融合
先前的多模态世界模型依赖于天真的融合方法[26, 90, 112]。我们的实验表明,基于Transformer架构的方法在预测任务上优于这种天真的方法。受最近的研究启发[15, 21, 86],我们采用了Transformer[100]架构的自注意机制来融合不同传感器的特征。Transformer接受一系列标记作为输入,其中每个标记是一个 D D D维特征向量,因此所需的输入序列为 t i n ∈ R D t × N t t_{in} ∈ \mathbb{R}^{D_t×N_t} tin∈RDt×Nt,其中 D t D_t Dt表示每个标记的特征维度, N t N_t Nt表示序列中的标记数。最初,我们展平了编码器中描述的特征 F F F的 H H H和 W W W维度,得到了与Transformer输入形状要求匹配的标记 f ∈ R C × H W f ∈ \mathbb{R}^{C×HW} f∈RC×HW。随后,我们为每个标记引入了2D正弦位置嵌入[15, 100] e ∈ R C × H W e ∈ \mathbb{R}^{C×HW} e∈RC×HW,以引入空间归纳偏差。此外,可学习的传感器嵌入 s ∈ R C × N s s ∈ \mathbb{R}^{C×N_s} s∈RC×Ns被添加到每个标记中,引入传感器类别,其中 N s = 2 N_s = 2 Ns=2是传感器的数量。得到了结果标记 t ∈ R C × H W t ∈ R^{C×HW} t∈RC×HW,其中每个标记 t i ( x , y ) = f i ( x , y ) + e i ( x , y ) + s i t_i(x, y) = f_i(x, y) + e_i(x, y) + s_i ti(x,y)=fi(x,y)+ei(x,y)+si,其中 i i i表示第 i i i个传感器, ( x , y ) (x, y) (x,y)表示该标记在传感器特征中的坐标索引。然后,这些来自所有传感器的标记被连接并输入到由 k k k层组成的Transformer编码器中,每层由多头自注意力、MLP和层归一化组成,得到新的标记 t n e w ∈ R C × H W t_{new} ∈ \mathbb{R}^{C×HW} tnew∈RC×HW。这些新的标记被重新塑造成原始输入特征的形状,即 F c n e w ∈ R C × H c × W c F^{new}_c ∈ \mathbb{R}^{C×H_c×W_c} Fcnew∈RC×Hc×Wc和 F L n e w ∈ R C × H L × W L F^{new}_L ∈ \mathbb{R}^{C×H_L×W_L} FLnew∈RC×HL×WL。然后,它们分别经过卷积层进行下采样,随后通过池化层获得1D特征 f d ∈ R D f_d ∈ \mathbb{R}^D fd∈RD。这两个特征向量,以及从提供的路线地图和速度信息中得到的1D特征,经过卷积层、MLP和池化层处理,然后连接在一起。这个连接的特征向量随后通过全连接层,以降低其维度,产生输入到过渡模型的一维向量 o t ∈ R D o_t ∈ \mathbb{R}^D ot∈RD。
5. 过渡模型( o t o_t ot)
最近的研究将世界建模表述为单个序列模型[41, 129],但这些方法在计算上非常耗费资源。为了得到一个更轻量级的模型,我们采用了MILE [40]和Dreamer [30, 31]中发现的基本架构。输入包括融合的观测特征 o 0 : t o_{0:t} o0:t 和编码后的动作 a 0 : t ∈ R T × D a a_{0:t} ∈ \mathbb{R}^{T ×D_a} a0:t∈RT×Da,基于一个简单的MLP,假设有一个策略或者运动规划器。输出包括隐藏状态 s 0 : t ∈ R T × D s s_{0:t} ∈ \mathbb{R}^{T ×D_s} s0:t∈RT×Ds 和确定性的历史状态 h 0 : t ∈ R T × D h h_{0:t} ∈ \mathbb{R}^{T ×D_h} h0:t∈RT×Dh,以及未来状态 s t : t + n s_{t:t+n} st:t+n 和 h t : t + n h_{t:t+n} ht:t+n 的预测。这里, T T T表示帧数,也被称为序列长度,而 D a D_a Da、 D s D_s Ds、 D h D_h Dh 分别是每个向量的维度。确定性历史变量 h t + 1 = f θ ( h t , s t ) h_{t+1} = f_θ(h_t, s_t) ht+1=fθ(ht,st) 通过门控循环单元(GRU)[16] f θ f_θ fθ 进行建模,使得模型能够记住过去的状态。后验隐藏状态概率分布由 q ( s t ∣ o ≤ t , a < t ) ∼ N ϕ ( o t , h t , a t ) q(s_t|o≤t, a<t) ∼ N_ϕ(o_t, h_t, a_t) q(st∣o≤t,a<t)∼Nϕ(ot,ht,at) 给出,而无观测特征 o t o_t ot 输入的先验隐藏状态概率分布由 p ( s t ∣ h t , a t − 1 ) ∼ N θ ( h t , a t − 1 ) p(s_t|h_t, a_{t−1}) ∼ N_θ(h_t, a_{t−1}) p(st∣ht,at−1)∼Nθ(ht,at−1) 给出。这里, N ϕ N_ϕ Nϕ 和 N θ N_θ Nθ 是由一个MLP建模的概率模型。最后,在观测存在的情况下, s t s_t st 从后验分布 q q q 中进行采样;而在观测缺失的情况下,即进行预测时, s ^ t \hat{s}_t s^t 从先验分布 p p p 中进行采样。
6. 多模态解码器
先前的世界模型解码为抽象表示[26, 40]、相机[33, 41]或激光雷达[129]数据。我们的模型不仅解码为高分辨率相机和激光雷达数据,还解码为与传感器无关的三维占据表示,表示物理世界的几何属性。我们解码器的输入是由过渡模型提供的具有形状 D t = D s + D h D_t = D_s + D_h Dt=Ds+Dh 的潜在动态状态 ( s t , h t ) (s_t, h_t) (st,ht)。
6.1 2D 解码器
由于我们将 RGB 图像和点云解码为形状为 C × H × W C × H × W C×H×W 的二维表示,我们能够同时使用相同的解码器架构,因为我们对激光雷达点云的距离视图表示是无损的,可以直接转换为三维表示。
首先,将输入重新调整为 D t × 1 × 1 D_t × 1 × 1 Dt×1×1,然后使用卷积解码器和一个核 K ∈ R H 0 × W 0 K ∈ \mathbb{R}^{H_0×W_0} K∈RH0×W0(其中 H 0 H_0 H0 和 W 0 W_0 W0 由最终输出分辨率 H × W H × W H×W 决定)来生成一个初始的二维特征,其维度为 C 0 × H 0 × W 0 C_0 × H_0 × W_0 C0×H0×W0。随后,我们使用类似于 [29, 31] 的卷积网络进行上采样,生成大小为 C n × H × W C_n × H × W Cn×H×W 的特征图。对于相机和激光雷达,我们使用了适应的核和头部。
6.2 3D 解码器
除了传感器数据,我们还解码为几何三维占据体素。先前的研究[50, 65]探索了受数据驱动视频预测启发的领域。相反,我们的方法在动作的条件下预测三维占据情况,从根本上利用对世界动态的更好理解。受到[40, 49]的启发,我们采用三维解码而不是二维解码。该方法使用可学习的张量 T 0 ∈ R C × X × Y × Z T_0 ∈ \mathbb{R}^{C×X×Y ×Z} T0∈RC×X×Y×Z,其中张量的大小 X × Y × Z X × Y × Z X×Y×Z 由最终体素网格大小决定, C C C 表示通道数,根据网络可调整。该张量逐渐上采样到目标体素网格大小。在每个上采样阶段,通过自适应实例归一化[49]将潜在状态 (st, ht) 注入到张量 T n T_n Tn 中(n 表示经过 n 次上采样阶段的张量)。三维占据表示可直接用于自动驾驶中的下游任务,如语义分割、目标检测或运动规划[22, 84, 89, 92, 127]。
通过自定义核 K K K 的大小或张量 T 0 T_0 T0 的大小,可以将二维和三维重建方法针对不同的输出分辨率进行定制。我们的预测的定性示例可在图 3 和 7 中找到。