343. 整数拆分
题目链接:343. 整数拆分
思路:动态规划五步曲
-
dp[i]:拆分数字i,可以得到的最大乘积为dp[i]。
-
递推公式:dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j))
从1遍历j,有两种渠道得到dp[i]:
一个是j * (i - j) 直接相乘。
一个是j * dp[i - j],相当于是拆分(i - j),对这个拆分不理解的话,可以回想dp数组的定义。
j怎么就不拆分呢?
j是从1开始遍历,拆分j的情况,在遍历j的过程中其实都计算过了。
-
初始化:从2开始,dp[2] = 1
题目提示:2 <= n <= 58
-
遍历顺序:i和j都是从前向后遍历
-
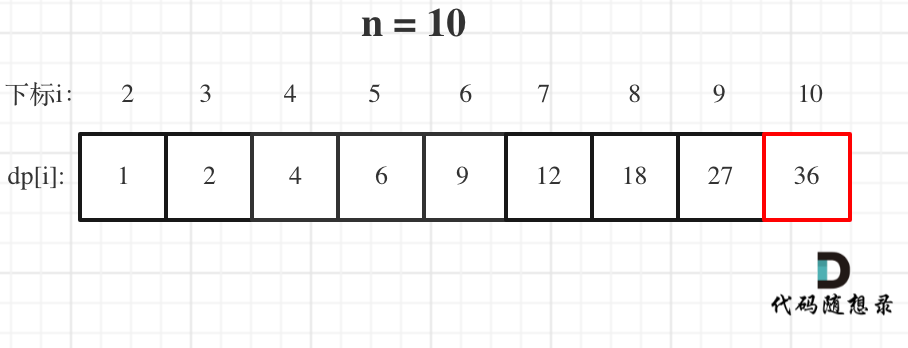
举例推导dp数组
当n为 10 的时候,dp数组里的数值,如下:
class Solution {public int integerBreak(int n) {// dp[i]:拆分数字i,可以得到的最大乘积为dp[i]。int[] dp = new int[n + 1];// 递推公式:j从1开始遍历,每次取j*(i - 1)和j*dp[i - j]中最大的// j * (i - j) 是单纯的把整数 i 拆分为两个数 i 和 i-j ,再相乘// 而j * dp[i - j]是将 i 拆分成两个以及两个以上的个数,再相乘。// 初始化:从2开始,dp[2] = 1dp[2] = 1;// 遍历顺序:i和j都是从前向后遍历for (int i = 3; i <= n; i++) {for (int j = 1; j <= i / 2; j++) {// 遇到大的便更新dp[i],dp[i] = Math.max(dp[i], Math.max(j * (i - j), j * dp[i - j]));}}return dp[n];}
}
因为拆分一个数n 使之乘积最大,那么一定是拆分成m个近似相同的子数相乘才是最大的。只不过我们不知道m究竟是多少而已,但可以明确的是m一定大于等于2,既然m大于等于2,也就是最差也应该是拆成两个相同的数,相乘之后可能是最大值。那么 j 遍历,只需要遍历到 n/2 就可以,后面就没有必要遍历了,一定不是最大值。
另一方面,枚举j的时候,是从1开始的。从0开始的话,那么让拆分一个数拆个0,求最大乘积就没有意义了。
96. 不同的二叉搜索树
题目连接:96. 不同的二叉搜索树
思路:动态规划五步曲(本题递推公式推导较为复杂,详情见代码随想录网站)
-
dp[i]:i个不同元素节点组成的二叉搜索树的个数为dp[i]
-
递推公式:dp[i] += dp[j - 1] * dp[i - j]
j 相当于是头结点的元素,从 1 遍历到 i 为止。
j-1 为 j 为头结点左子树节点数量,i-j 为以 j 为头结点右子树节点数量
-
初始化:dp[0] = 1
只需要初始化dp[0]就可以了,推导的基础,都是dp[0]。
-
遍历顺序是 i 从 1 到 n ,j 从 1 到 i 。
那么遍历 i 里面每一个数作为头结点的状态,用 j 来遍历 i 。
-
举例推导dp数组
n为5时候的dp数组状态如图:
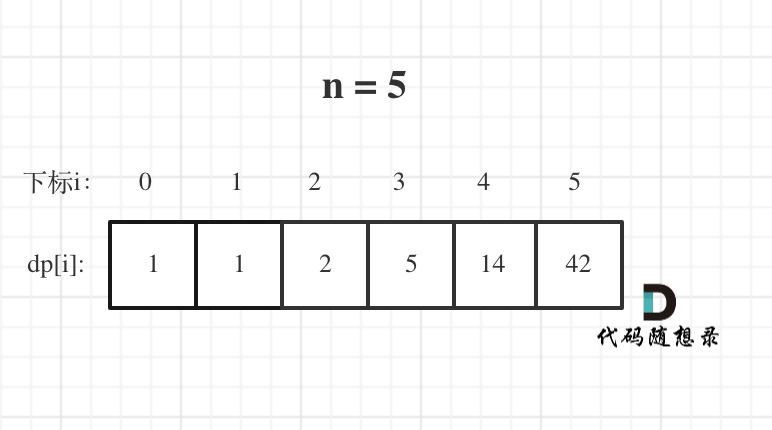
基本举例到n为3就可以了,n为4的时候,画图已经比较麻烦了。
class Solution {public int numTrees(int n) {// i个不同元素节点组成的二叉搜索树的个数为dp[i]int[] dp = new int[n + 1];// 递推公式:dp[i] += dp[j - 1] * dp[i - j]// 初始化:dp[0] = 1dp[0] = 1;// 遍历顺序for (int i = 1; i <= n; i++) {for (int j = 1; j <= i; j++) {dp[i] += dp[j - 1] * dp[i - j];}}return dp[n];}
}
也可以用定义递归函数的方法解决本题,代码如下:
class Solution {// 存在重叠子问题,可以通过备忘录的方式消除冗余计算。int[][] memo;/* 主函数 */public int numTrees(int n) {// 备忘录的值初始化为 0memo = new int[n + 1][n + 1];return count(1, n);}/* 计算闭区间 [lo, hi] 组成的 BST 个数 */int count(int lo, int hi) {// base caseif (lo > hi) return 1;// 查备忘录if (memo[lo][hi] != 0) {return memo[lo][hi];}int res = 0;for (int mid = lo; mid <= hi; mid++) {// mid 的值作为根节点 rootint left = count(lo, mid - 1);int right = count(mid + 1, hi);// 左右子树的组合数乘积是 BST 的总数res += left * right;}// 将结果存入备忘录memo[lo][hi] = res;return res;}
}