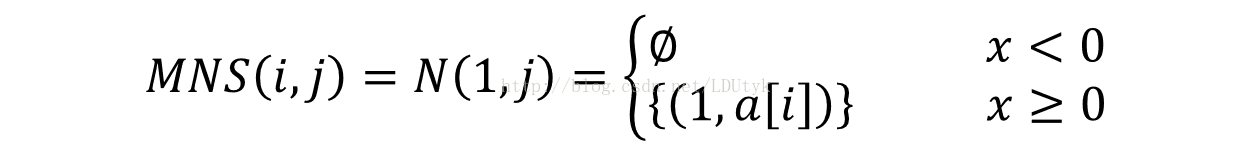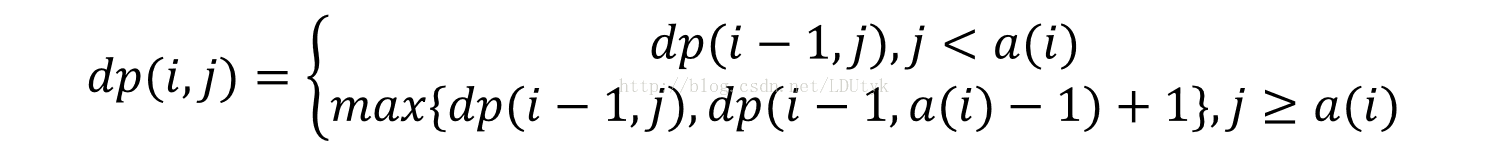3-8电路布线

问题描述

在一块电路板的上、下两端分别有n个接线柱。根据电路设计，要求用导线将上端接线柱与下端接线柱相连

借用https://blog.csdn.net/LDUtyk大佬的图片

如上图所示, 上端 i 节点与下端Ω(i) 节点相连, 但是要求连线不能交叉。Ω（x）是一个无序的排列。
制作电路板时候，会有N个绝缘层。要求将这n条连线分布到若干绝缘层上。在同一层上的连线不相交。
这个问题是要确定将哪些连线安排在第一层上，使得该层上有尽可能多的连线（不相交）。

例如
如图，上端节点 i 分别是1到10。下端节点Ω（i）为{8, 7, 4, 2, 5, 1, 9, 3, 10, 6}。
假如在同一绝缘层上端与下端节点相连并且不相交，只能使下端Ω（i）成递增序列。
则下端节点：
8， 9， 10 可在同一绝缘层
7， 9， 10可在同一绝缘层
4，5，9，10可在同一绝缘层
4， 5， 6也可在同一绝缘层
假如不是递增序列，如
在这里插入图片描述
很明显， 3， 1， 2就不能在同一绝缘层上，因为会相交。

记N（i，j）{（t，a(t)） | t<=i，a(t)<=j }代表上接线柱小于等于i并且下接线柱小于等于j的连线的集合。N（i，j）的最大不相交子集为MNS（i，j），假设MNS（i，j）中的连线数目为dp[i][j];
下面对MNS（i，j）进行判断区分：

（2）当i >1时
①j<a（i）。
此时，（i，a（i））不属于MNS（i，j）。故在这时，MNS（i，j） =MNS（i-1， j），从而dp（i，j）=dp（i-1，j）。
②j >=a(i)。
若(i, a(i))∈MNS(i,j)，则对任意(t, a(t))∈MNS(i,j)有t <i且a(t)<a(i)；否则，(t,a(t))与(i,a(i))相交。在这种情况下MNS(i,j)-{(i,a(i))}是N(i-1,a(i)-1)的最大不相交子集。否则，子集MNS(i-1,a(i)-1)∪{(i,a(i))}包含于N(i,j)是比MNS(i,j)更大的N(i,j)的不相交子集。这与MNS(i,j)的定义相矛盾。
若(i, a(i))不属于MNS(i,j)，则对任意(t, a(t))∈MNS(i,j)，有t<i。从而MNS(i,j)包含于N(i-1,j)，因此，dp(i,j)≤dp(i-1,j)。另一方面，MNS(i-1,j)包含于N(i,j),故又有dp(i,j)≥dp(i-1,j)，从而Size（i,j）=Size(i-1,j)。
（i，a[i]）属于MNS(i,j)，则dp(i,j)=dp(i-1,a[i])+1;
在这里插入图片描述
用动态规划写
上代码

#include <bits/stdc++.h>using namespace std;int main() {//初始化 int down[11] = {0, 8, 7, 4, 2, 5, 1, 9, 3, 10, 6};int MAX[11][11];//初始化MAX的底 for(int i = 1; i < 11; i ++) {if(i < down[1]) {MAX[1][i] = 0;} else {MAX[1][i] = 1;}}for(int i = 2; i < 11; i ++) {	//遍历上端for(int j = 1; j < 11; j ++) {	//遍历下端if(j < down[i]) {MAX[i][j] = MAX[i - 1][j];} else {int a = MAX[i - 1][down[i] - 1] + 1;int b = MAX[i - 1][j];MAX[i][j] = a > b ? a : b;}}}cout << MAX[10][10] << endl;return 0;
}