Leetcode -746.使用最小花费爬楼梯

题目：给你一个整数数组 cost ，其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用，即可选择向上爬一个或者两个台阶。
你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。
请你计算并返回达到楼梯顶部的最低花费。

示例 1：
输入：cost = [10, 15, 20]
输出：15
解释：你将从下标为 1 的台阶开始。

• 支付 15 ，向上爬两个台阶，到达楼梯顶部。
  总花费为 15 。

示例 2：
输入：cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1]
输出：6
解释：你将从下标为 0 的台阶开始。

• 支付 1 ，向上爬两个台阶，到达下标为 2 的台阶。
• 支付 1 ，向上爬两个台阶，到达下标为 4 的台阶。
• 支付 1 ，向上爬两个台阶，到达下标为 6 的台阶。
• 支付 1 ，向上爬一个台阶，到达下标为 7 的台阶。
• 支付 1 ，向上爬两个台阶，到达下标为 9 的台阶。
• 支付 1 ，向上爬一个台阶，到达楼梯顶部。
  总花费为 6 。

提示：
2 <= cost.length <= 1000
0 <= cost[i] <= 999

思路是动态规划，因为每次可以爬一个台阶，也可以爬两个台阶，所以每次取前两个台阶花费的较小值，再加上当前台阶需要的花费，就是当前的总花费；

如图，就数据 [1,100,1,1,1,100,1,1,100,1] 来说，初始应该是从第一个台阶开始走两个台阶，到 dpi，dpi 就是当前的总花费：

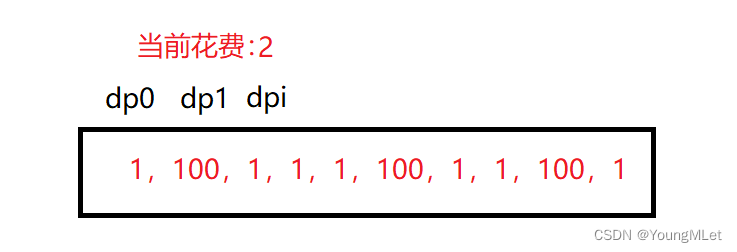
向后迭代，当前 dpi 取前两个值的较小值，再加上当前台阶的花费，就是当前新的的总花费了，即 3；这一步相当于计算从当前台阶 dp1 走一步到 dpi 需要的花费；

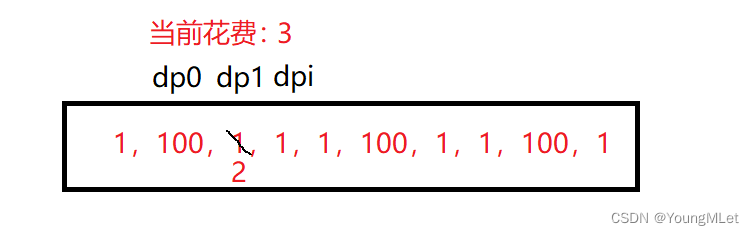
继续迭代，计算从当前的台阶 dp1 走一步到 dpi 这个台阶需要的花费 dpi；

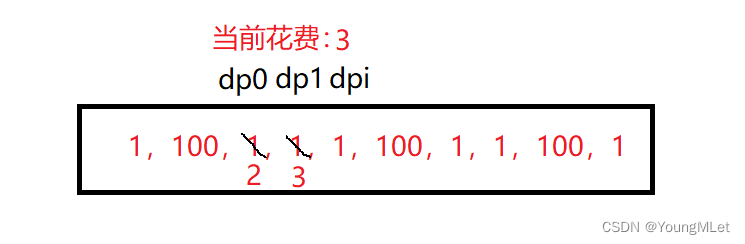
就每次走一步，计算出 dpi 的较小值，这个 dpi 又作为下一个台阶判断的较小值的标准，这样迭代后面只剩下 dp0 和 dp1 最后两个台阶，取较小值即是最小的总花费；

		int minCostClimbingStairs(int* cost, int costSize){//定义第一个台阶和第二个台阶分别为 dp0 和 dp1int dp0 = cost[0], dp1 = cost[1];//动态规划//i从第三个台阶开始遍历，因为 dp0 和 dp1 走一个台阶或者两个台阶都可以到第三个台阶//dpi 取 dp0 和 dp1 的较小值，再加上当前台阶需要的花费，就为当前的总花费//然后迭代，将 dpi 赋给 dp1 ，dp1 赋给 dp0 ，dpi继续取前两个的较小值for (int i = 2; i < costSize; i++){int dpi = fmin(dp0, dp1) + cost[i];dp0 = dp1;dp1 = dpi;}//到最后的两个台阶，取较小的花费即可，因为最后两个台阶可以直接到顶部return fmin(dp0, dp1);}

Leetcode -747.至少是其他数字两倍的最大数

题目：给你一个整数数组 nums ，其中总是存在 唯一的 一个最大整数 。

请你找出数组中的最大元素并检查它是否 至少是数组中每个其他数字的两倍 。如果是，则返回 最大元素的下标 ，否则返回 - 1 。

示例 1：
输入：nums = [3, 6, 1, 0]
输出：1
解释：6 是最大的整数，对于数组中的其他整数，6 至少是数组中其他元素的两倍。6 的下标是 1 ，所以返回 1 。

示例 2：
输入：nums = [1, 2, 3, 4]
输出： - 1
解释：4 没有超过 3 的两倍大，所以返回 - 1 。

示例 3：
输入：nums = [1]
输出：0
解释：因为不存在其他数字，所以认为现有数字 1 至少是其他数字的两倍。

提示：
1 <= nums.length <= 50
0 <= nums[i] <= 100
nums 中的最大元素是唯一的

思路是找出数组中的最大元素以及第二大的元素，判断最大元素是否大于两倍的第二大元素，如果是则返回提前记录的最大元素的下标，否则返回 -1；

		int dominantIndex(int* nums, int numsSize){//定义 max 为最大的元素，secmax 为第二大的元素，index 为最大元素的下标int max = -1, secmax = -1, index = 0;//遍历数组for (int i = 0; i < numsSize; i++){//如果当前元素大于 max ，先将 max 赋给 secmax//再将当前元素赋给 max，下标赋给 indexif (nums[i] > max){secmax = max;max = nums[i];index = i;}//当这个元素大于第二大的元素，而小于最大元素的时候，将这个元素赋给 secmaxelse if (nums[i] > secmax){secmax = nums[i];}}//最后判断 max 是否大于两倍的 secmax，再返回对应的值return max >= 2 * secmax ? index : -1;}