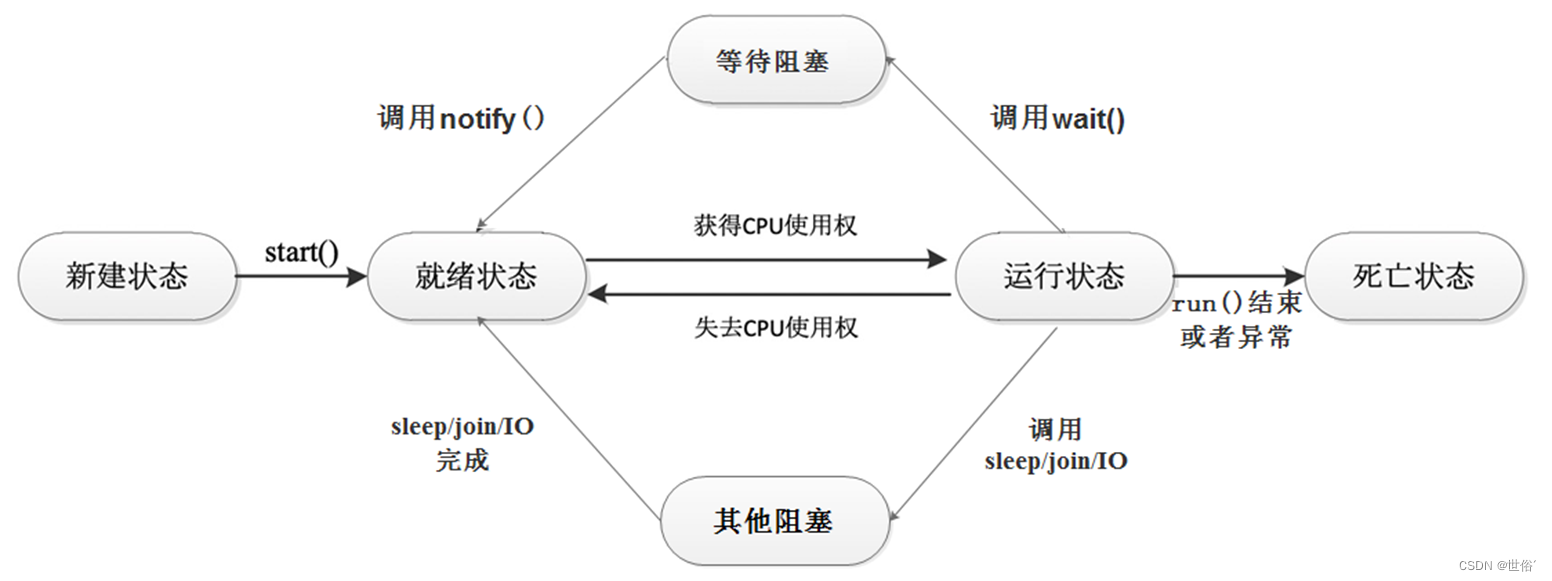
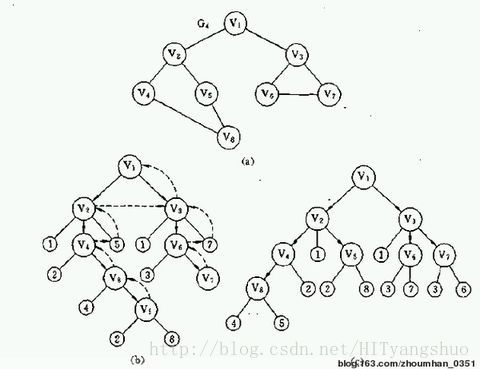
1. 深度优先搜索（DFS）是搜索手段之一。是从某个状态开始不断转移状态直到无法转移为止，然后退回到前一步状态继续转移其他状态，可以想象为一个沿树爬行的虫子，在一个交叉口他会首先随机选择一条分岔路口一直走下去直到死路为止，然后会返回到这个交叉口沿着另一条分支爬行下去，直到遍历所有可能的路径为止。根据这个特点，DFS算法用递归来实现比较简单。

以下例题说明

• Lake Counting（POJ）
  有一个大小为N*M的园子，雨后积水。八连通的积水被认为是连接在一起的。请求出园子里总共有多少水洼？（八连通指的是下图中相对W的A部分）
  AAA
  AWA
  AAA
  样例输入N=10，M=12，园子如下：
  w … … . . ww .
  . www … . . www
  … . ww … ww .
  … … … ww .
  … … … w . .
  . . w … … w . .
  . w . w … . . ww .
  w . w . w … . . w .
  . w . w … … w .
  . . w … … . w .
  输出 3
  
  • 解析：从任意w开始，不停把邻接部分用’.’代替。一次DFS后与初始的这个w连接的所有w就都被替换成了’.’，因此直到图中不再存在w为止，总共进行DFS的次数就是答案了。八个方向共对应了8种状态转移，每个格子DFS参数至多被调用一次。
  • 以下是部分答案片段，没写输入输出流以及主函数，但是主要功能函数在下面

#include <iostream>
#include <cstdio>
using namespace std;//输入
int N,M;
char field[MAX_N][MAX_M + 1]; // 园子void dfs (int x,int y)  //现在位置（x，y）
{field[x][y] = '.';   //将现在位置替换为‘.’for(int dx = -1; dx <= 1; dx++)  //循环遍历移动的8个方向{for(int dy = -1; dy <= 1; dy++){int nx = x + dx,ny = y + dy;  //向x方向移动dx，向y方向移动dy，移动结果为（nx，ny）if( 0 <= nx && nx <=N && 0 <=ny && ny <=M && field[nx][ny] == 'w')        //判断点是不是在院子内以及是否有积水dfs(nx, ny);}}return;
}
void solve()
{int res = 0;for(int i = 0; i < N; i++){for(int j = 0; j < M; j++){if (field[i][j] == 'w'){dfs(i, j);   // 从有w的地方开始dfsres++;}}}printf("%d\n", res);
}