一、递归最小二乘法

递推最小二乘法：当矩阵维数增加时，矩阵求逆运算计算量过大，而且不适合在线辨识。为了减少计算量，并且可以实时地辨识出动态系统的特性，可以将最小二乘法转换成参数递推的估计。

取前N组数据，然后从N+1项后向后迭代，当前估计值=上一次估计值+修正值。

给定过程：
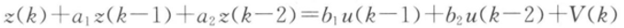式中，理想的系数值a1=1.5,a2=0.7,b1=1.0和b2=0.5。V(k)服从N(0,1)的随机噪声。

clear all
close all
clc
%产生N(0,1)正态分布的随机噪声
randn('seed',100);
v=randn(1,60); %产生M序列
L=60;% M序列的周期
y1=1;y2=1;y3=1;y4=0;%四个移位积存器的输出初始值
for i=1:L;
x1=xor(y3,y4);
x2=y1;x3=y2;x4=y3;y(i)=y4;if y(i)>0.5,u(i)=-5;%M序列的幅值为5else u(i)=5;endy1=x1;y2=x2;y3=x3;y4=x4;
end 
figure(1);
stem(u),grid on
% 递推最小二乘辨识程序
z(2)=0;z(1)=0;
%观测值由理想输出值加噪声
for k=3:60;%循环变量从3到15   z(k)=-1.5*z(k-1)-0.7*z(k-2)+u(k-1)+0.5*u(k-2)+0.5*v(k); 
end
%RLS递推最小二乘辨识
c0=[0.001 0.001 0.001 0.001]';
p0=10^3*eye(4,4);
E=0.000000005;%相对误差
c=[c0,zeros(4,59)];%被辨识参数矩阵的初始值及大小
e=zeros(4,60);%相对误差的初始值及大小
lamt=1;
for k=3:60; h1=[-z(k-1),-z(k-2),u(k-1),u(k-2)]';k1=p0*h1*inv(h1'*p0*h1+1*lamt);%求出K的值new=z(k)-h1'*c0; c1=c0+k1*new;%求被辨识参数cp1=1/lamt*(eye(4)-k1*h1')*p0;e1=(c1-c0)./c0;%求参数当前值与上一次的值的差值e(:,k)=e1; %把当前相对变化的列向量加入误差矩阵的最后一列    c(:,k)=c1;%把辨识参数c 列向量加入辨识参数矩阵的最后一列 c0=c1;%新获得的参数作为下一次递推的旧参数p0=p1;if norm(e1)<=E break;%若参数收敛满足要求，终止计算end
end
%分离参数
a1=c(1,:); a2=c(2,:); b1=c(3,:); b2=c(4,:); 
ea1=e(1,:); ea2=e(2,:); eb1=e(3,:); eb2=e(4,:); 
figure(2);
i=1:60;
plot(i,a1,'k',i,a2,'b',i,b1,'r',i,b2,'g') %画出辨识结果
legend('a1','a2','b1','b2');
title('递推最小二乘参数辨识')
figure(3); 
i=1:60; 
plot(i,ea1,'k',i,ea2,'b',i,eb1,'r',i,eb2,'g') %画出辨识结果的收敛情况
legend('a1','a2','b1','b2');
title('辨识精度')

二、增广最小二乘法

增广最小二乘法：当噪声均值为0时，最小二乘法参数估计算法为无偏估计，为了解决最小二乘法参数估计的有偏性，将噪声模型的辨识同时考虑进去，就是增广最小二乘法。

增广最小二乘法相当于参数向量和数据向量维数扩大了的最小二乘法，它能在有色噪声(可用平均滑动模型来表示)情况下给出参数的一致估计量，同时可以把噪声模型也辨识出来。

给定过程：

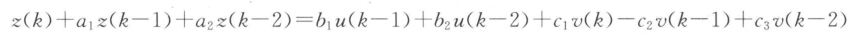
式中，理想的系数值a1=1.5,a2=0.7,b1=1.0和b2=0.5,c1=1.2,c2=-1.0,c3=0.2。V(k)服从正态分布的白噪声N(0,1)，输入信号采用4阶M序列，其幅值为1。

clear all
close all
clc% M序列、噪声信号产生及其显示程序 
L=60;%四位移位积存器产生的M序列的周期
y1=1;y2=1;y3=1;y4=0;
for i=1:L;x1=xor(y3,y4);x2=y1;x3=y2;x4=y3;y(i)=y4;if y(i)>0.5,u(i)=-1;else u(i)=1;endy1=x1;y2=x2;y3=x3;y4=x4;
end
figure(1);
stem(u),grid on%画出M序列输入信号
randn('seed',100)
v=randn(1,60); %产生一个N（0,1）的随机噪声
%增广递推最小二乘辨识
z(2)=0;z(1)=0;
theat0=[0.001 0.001 0.001 0.001 0.001 0.001 0.001]';%直接给出被辨识参数的初始值,即一个充分小的实向量
p0=10^4*eye(7,7);%初始状态P0
theat=[theat0,zeros(7,59)];%被辨识参数矩阵的初始值及大小
for k=3:60; z(k)=-1.5*z(k-1)-0.7*z(k-2)+u(k-1)+0.5*u(k-2)+1.2*v(k)-v(k-1)+0.2*v(k-2)  h1=[-z(k-1),-z(k-2),u(k-1),u(k-2),v(k),v(k-1),v(k-2)]';x=h1'*p0*h1+1;x1=inv(x); k1=p0*h1*x1; %Kd1=z(k)-h1'*theat0; theat1=theat0+k1*d1;%辨识参数c theat0=theat1;%给下一次用theat(:,k)=theat1;%把辨识参数c 列向量加入辨识参数矩阵 p1=p0-k1*k1'*[h1'*p0*h1+1];%find p(k)p0=p1;%给下次用end%循环结束%分离变量a1=theat(1,:); a2=theat(2,:); b1=theat(3,:); b2=theat(4,:);c1=theat(5,:); c2=theat(6,:); c3=theat(7,:); 
i=1:60;    
figure(2);
plot(i,z)
figure(3)
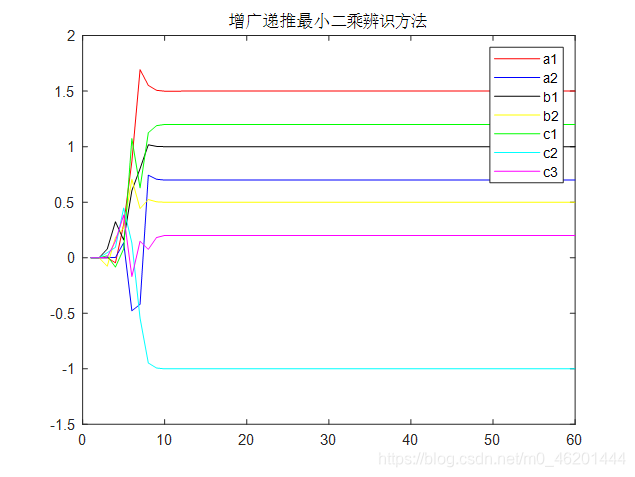
plot(i,a1,'r',i,a2,'b',i,b1,'k',i,b2,'y',i,c1,'g',i,c2,'c',i,c3,'m')%画出各个被辨识参数
title('增广递推最小二乘辨识方法')%标题

三、带遗忘因子的递归增广最小二乘法的参数估计

遗忘因子算法的基本思想为：对老数据乘以遗忘因子，以降低老数据所提供的信息量，增加新数据的信息量。前一时刻的数据乘以较小的权，后一时刻的数据乘以较大的权，表示对新的数据较为重视，对老数据所起的作用逐渐削弱。

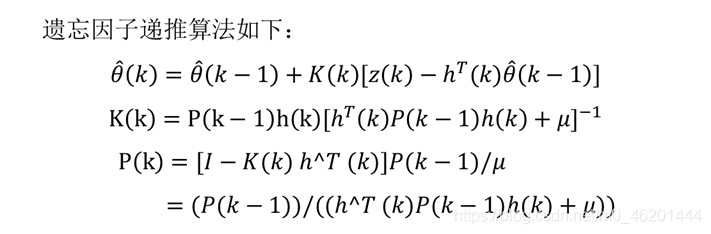
%开环系统参数辨识，带遗忘因子的递推最小二乘估计法（FFRLS)，系统为单入单出的CAR(带控制量的自回归模型）模型,三阶系统
clear all
clc
a=[1 -1.1 0.6 0.1];b=[1 0.7];d=4; %实际模型系数矩阵与纯迟延
L=1000;                           %仿真长度
na=length(a)-1;nb=length(b)-1;    %na,nb为输出输入系数矩阵A,B的阶数
yk=zeros(na,1);                   %输出矩阵初始化
yk_m=zeros(na,1);                 %模型输出
uk=zeros(nb+d,1);                 %输入矩阵初始化
theta_e0=zeros(na+nb+1,1);        %theta_e0为估计参数初值，a1,a2....an,b0,b1,...bn,共na+nb+1个
phi=zeros(na+nb+1,1);             %phi为当前实际输出输入构成的矩阵
P=10^6*eye(na+nb+1);              %修正系数初值
beta=0.99;                        %遗忘因子，在0.95到1之间
u=randn(L,1);                     %输入信号，方差为1的白噪声序列
omega=sqrt(0.1)*randn(L,1);       %干扰信号，方差为0.1的白噪声序列for i=1:Ltheta(:,i)=[a(2:na+1),b]';    %系统实际参数值phi=[-yk;uk(d:d+nb)];         %系统输出输入矩阵phi_e=[-yk_m;uk(d:d+nb)];     %模型输出输入矩阵y(i)=phi'*theta(:,i)+omega(i);%系统实际输出y_m(i)=phi_e'*theta_e0;       %模型输出%递推公式K=P*phi/(beta+phi'*P*phi);   theta_e(:,i)=theta_e0+K*(y(i)-phi'*theta_e0);P=(eye(na+nb+1)-K*phi')*P/beta;%数据更新theta_e0=theta_e(:,i);for j=na:-1:2yk(j)=yk(j-1);yk_m(j)=yk_m(j-1);endyk(1)=y(i);yk_m(1)=y_m(i);for j=(nb+d):-1:2uk(j)=uk(j-1);enduk(1)=u(i);
endfigure
x=[1:L];
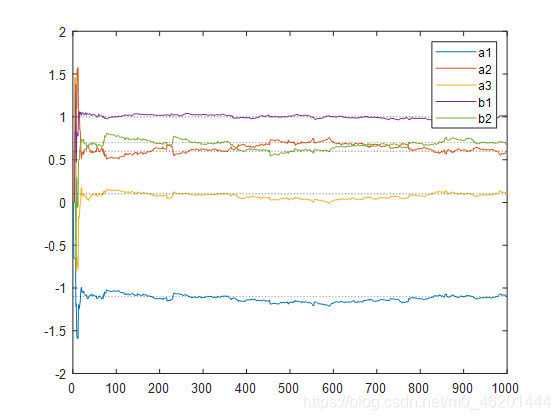
plot(x,theta_e,x,theta,'k:');
legend('a1','a2','a3','b1','b2');
axis([0 L -2 2]);
figure
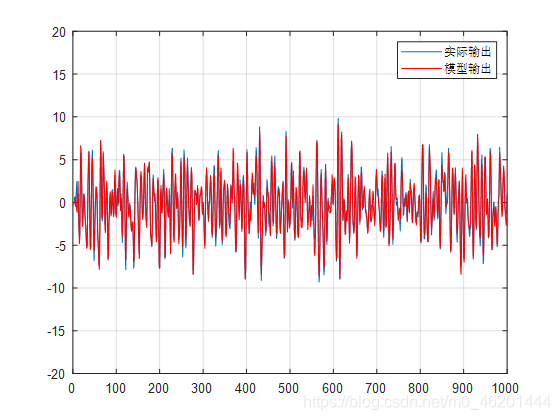
plot(x,y,x,y_m,'r');
legend('实际输出','模型输出');
axis([0 L -20 20]);
grid on;

参考文献：

[1]方桂花,王鹤川,高旭.基于动态遗忘因子递推最小二乘法的永磁同步电机参数辨识算法[J].计算机应用与软件,2021,38(01):280-283.
[2]冯亦奇,陈勇.基于遗忘因子的UKF车辆状态参数估计算法[J].合肥工业大学学报(自然科学版),2020,43(11):1450-1455+1499.
[3]焦慧方,陈希亮,高敏,马忠玲.基于带遗忘因子交替广义最小二乘法的多变量耦合系统参数辨识[J].咸阳师范学院学报,2018,33(02):49-53.