预备知识

1.关于z3

Z3是一个微软出品的开源约束求解器，能够解决很多种情况下的给定部分约束条件寻求一组满足条件的解的问题（可以简单理解为解方程的感觉，虽然这么比喻其实还差距甚远，请勿吐槽），功能强大且易于使用，本文以近期的CTF题为实例，向尚未接触过约束求解器的小伙伴们介绍Z3在CTF解题中的应用。
Z3约束求解器是针对Satisfiability modulotheories Problem的一种通用求解器。所谓SMT问题，在Z3环境下是指关于算术、位运算、数组等背景理论的一阶逻辑组合决定性问题。虽然Z3功能强大，但是从理论上来说，大部分SMT问题的时间复杂度都过高，根本不可能在有限时间内解决。所以千万不要把Z3想象得过于万能。
Z3在工业应用中实际上常见于软件验证、程序分析等。然而由于功能实在强大，也被用于很多其他领域。CTF领域来说，能够用约束求解器搞定的问题常见于密码题、二进制逆向、符号执行、Fuzzing模糊测试等。此外，著名的二进制分析框架angr也内置了一个修改版的Z3。
Z3本身提供一个类似于Lisp的内置语言，但是实际使用中，一般使用Python Binding操作会比较方便。

实验目的

通过该实验了解z3的常规使用、IDA Pro、file等工具的使用，以及z3在CTF中的使用技巧。

实验环境

Windows 8（安装ida）
kali IP地址：随机分配
源码请在实验机内下载使用：http://tools.hetianlab.com/tools/z3.zip

实验步骤一

z3的安装方法（已装）：

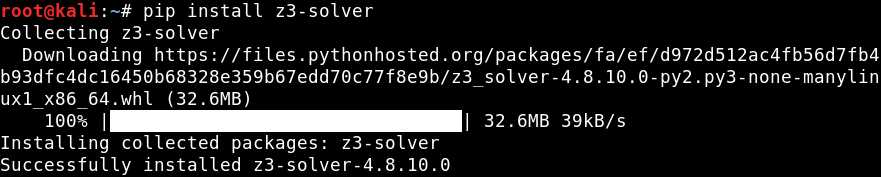
我们首先以一个简单的例子来入门z3最基础的用法：

函数Int(‘x’)在Z3中创建了一个名为x的整形变量，solve函数则处理一系列约束（即已知条件），上面的例子使用两个变量x和y以及三个约束。可以理解为z3用来解方程，solve中是方程满足的条件。
接下来的例子可以学习到z3在约束求解中的其他功能。
z3表达式简化器（用于简化表达式）：

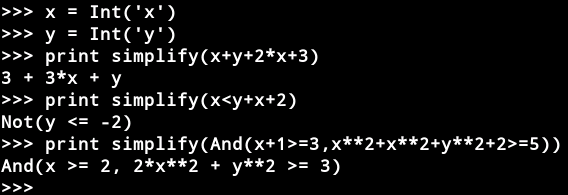
（**是次方的意思）
z3提供了用于遍历表达式的函数：

z3可用于求解非线性多项式约束：

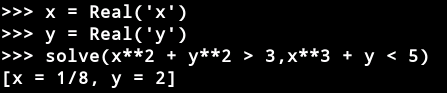
Real(’x’)创建实数变量x。Z3可以表示任意大的整数，有理数（如上例）和无理代数。一个无理数代数是具有整数系数的多项式的根。在内部，Z3精确地代表了所有这些数字。无理数以十进制表示法显示，以便读取结果：

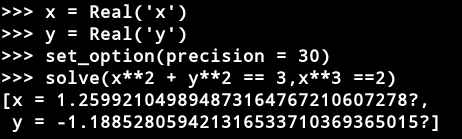
函数set_option用于配置Z3环境。它用于设置全局配置选项，比如设置结果如何显示。set_option(precision = 30)设置显示结果时使用的小数位数为30。而?标记在1.2599210498?中表示输出被截断。
如果一个约束没有解决方案（可理解为方程没有解）则显示如下：

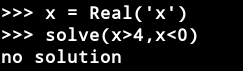
求解器API的使用：

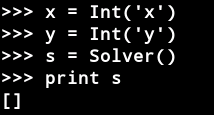
solver()创建一个通用的求解器。

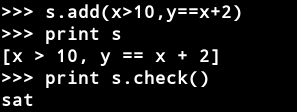
可以使用add()添加约束。我们说约束已经在求解器中断言，方法check()判断是否有解解决断言的约束。如果找到解，则结果是SAT（可满足）。如果没有解存在，则结果是UNSAT（不可满足），也可以说断言约束系统是不可行的。
了解了这些基础之后，以一个数学物理问题结尾吧。
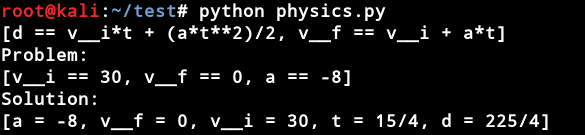
甲正以30.0米/秒的速度行驶，红绿灯变成黄色，甲刹车。如果甲的加速度为-8.00 m / s^2，求车辆在打滑过程中的位移。
代码如下：

运行结果为：

实验步骤二

任务描述：使用z3尝试按照给出的约束破解序列码，序列码格式为XXXX-XXXX-XXXX-XXXX（我们提供了源程序和可执行文件）。
我们先执行一下看看效果：

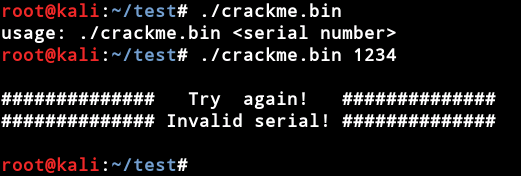
可以看到，执行时要求输入正确的序列号，否则会报错。
我们直接来看题目提供的源程序，来梳理下序列号产生的逻辑：

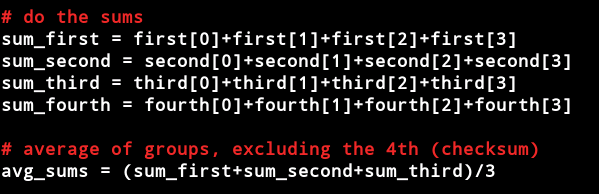
从代码中我们可以判断出序列号需要满足的约束条件：
1）x在0-9之间，但是第四组的x一定在3-8之间；
2）第四组是校验和，他的总和等于前三组的平均值，它的平均值等于第一组的总和；
3）第一组的总和和第二组的总和不同；
4）第一组和第四组相同下标的值不同；
5）第二组和第三组相同下标的值不同。
当然我们可以暴力破解，不过我们现在可以使用z3来解决这个问题。
Z3有几种类型，如Int，Float，IntVector等。在这里，我决定为每组四个使用一个IntVector。第一个参数是Z3变量名，第二个是矢量大小。稍后使用Z3变量名来访问生成的模型中的值。

求解器将负责应用约束并获取模型：

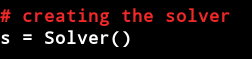
因为我们需要使用总和和平均值来计算和存储这些值。我们仅将第四组用于校验和。

现在我们准备好了这些值，让我们添加约束，只需使用求解器实例中的add()即可。

以下是我在addConstraintBetweenXandY和addConstraintNotEq上面使用的两个简单的自定义函数，用于遍历符合约束的值。
现在我们已完成约束，我们已准备好获得我们的解。在打印模型之前，必须调用check()以确保至少有一个令人满意的解，并且还因为它能判断已有的约束是否能够求解：

这是完整的原始输出：

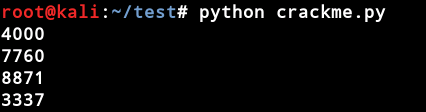
还记得我们在开始时声明的变量吗？所以现在我们以[variableName__index = value，…]的形式得到了我们的序列，这足以解决这个问题。但我们只是格式化它们。为此，需要使用索引（a__0，a__1，…）来访问这些值。可以使用Python变量作为索引检索这些内容获得序列号：

运行结果如图：

然后把得到的序列号输入crackme：

可以看到序列号是有效的。

实验步骤三

任务描述：再来做一个crackme吧~（这次只提供可执行文件）
先执行看看：

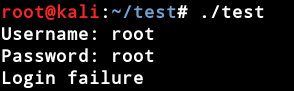
程序要求我们输入用户名和密码，如果校验出错则提出login failure。
我们切换到win中用IDA分析。
在切换之前，先使用file来看一下相关信息：

是64位的，所以使用ida pro x64打开：

点击ok即可：

先f5反编译main函数：

可以看到是checkuser2函数用于判断用户名和密码并决定我们登录是否成功，我们跟进去看看：

可知用户名为Palash2。
v6是一个常量数组，用于在循环内进行计算。在每次迭代时，v4应为0，以使其成为有效的用户名/密码组合。让我们尝试删除无用的片段，来获得更清晰的for循环的逻辑：

根据这个逻辑，按照第一个crackme一样用python表达同样的逻辑，从正向出发去考虑求解。
代码如图：

运行后结果如图：

在test可执行文件里测试：

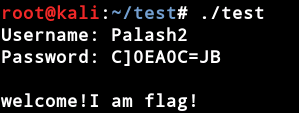
成功拿到了flag。