比如
select ' 1+(2-3)+(-4.1-3.1)-(4-3)-(-3.3+4.3)-1 ' col ,1+(2-3)+(-4.1-3.1)-(4-3)-(-3.3+4.3)-1 result
 \
\
现在的需求式 给你一个字符串如上述col 你要算出result。
前提式 只有+和-的运算,而且只有嵌套一次 -(4-3)没有 -(-4+(3-(3+1)))嵌套多次。
第一步我们需要将运算拆分为每一个单独的计算例如上述拆分为
1
+(2-3)
+(4.1-3.1)
-(4-3)
-(-3.3+4.3)
-1
这几部分,然后记住前面的符号,
第二部再将这几部分中的计算再拆分。
例如 +(2-3) 拆分为2 + -3
-(4-3) 差分为 4-3结果为 4 + -3 因为括号前面是负号 改为 negtive(4) +negtive(-3)。
总体思路就是将每一个单独的数字得出其正负,然后所有数字相加。
涉及到的语法有 lateral view 一行变多行
split 如何拆分整个算式。
substring/translate去除掉括号
其中最难点在于split。
第一步如何split? 我们将一个表达式拆分
'1+(2-3)+(-4.1-3.1)+13-(4-3)-(-3.3+4.3)-11' 如何拆分为下面的数组
["1","+(2-3)","+(-4.1-3.1)","+13","-(4-3)","-(-3.3+4.3),-11"]
我们首先根据什么split? + - 还是+( ,)-
说实话这个玩意是真的难写。
select split( '1+(2-3)+(-4.1-3.1)-(4-3)-(-3.3+4.3)','(?=([\\-\\+]\\())')
结果 ["1","+(2-3)","+(-4.1-3.1)","-(4-3)","-(-3.3+4.3)"]
看着好像是全部拆分了,以为没问题的时候,又发现了问题
select split( '1+(2-3)+(-4.1-3.1)+3-(4-3)-(-3.3+4.3)','(?=([\\-\\+]\\())')
结果 ["1","+(2-3)","+(-4.1-3.1)+3","-(4-3)","-(-3.3+4.3)"]
这里这个+3没有单独的分组
经过改进
select split( '1+(2-3)+(-4.1-3.1)+3-(4-3)-(-3.3+4.3)','(?=([\\-\\+]\\())|(?=[\\-\\+]\\d+[\\-\\+])')
["1","+(2-3)","+(-4.1-3.1)","+3","-(4-3)","-(-3.3+4.3)"]
然后又发现了问题
select split( '1+(2-3)+(-4.1-3.1)+3-(4-3)-(-3.3+4.3)+11','(?=([\\-\\+]\\())|(?=[\\-\\+]\\d+[\\-\\+])')
["1","+(2-3)","+(-4.1-3.1)","+3","-(4-3)","-(-3.3+4.3)+11"]
--说实话这个b正则式真难写
最后为
select split( '1+(2-3)+(-4.1-3.1)+3-(4-3)-(-3.3+4.3)-11','(?=([\\-\\+]\\())|(?=[\\-\\+]\\d+($|[\\+\\-]))')
["1","+(2-3)","+(-4.1-3.1)","+3","-(4-3)","-(-3.3+4.3)","-11"]
接着是要拆分括号里的计算
select split( a ,'(?=[+-]\\d)')
from (
select '1+2+3' a union all select '1-2+3' union all select '-1-1-3'
)t
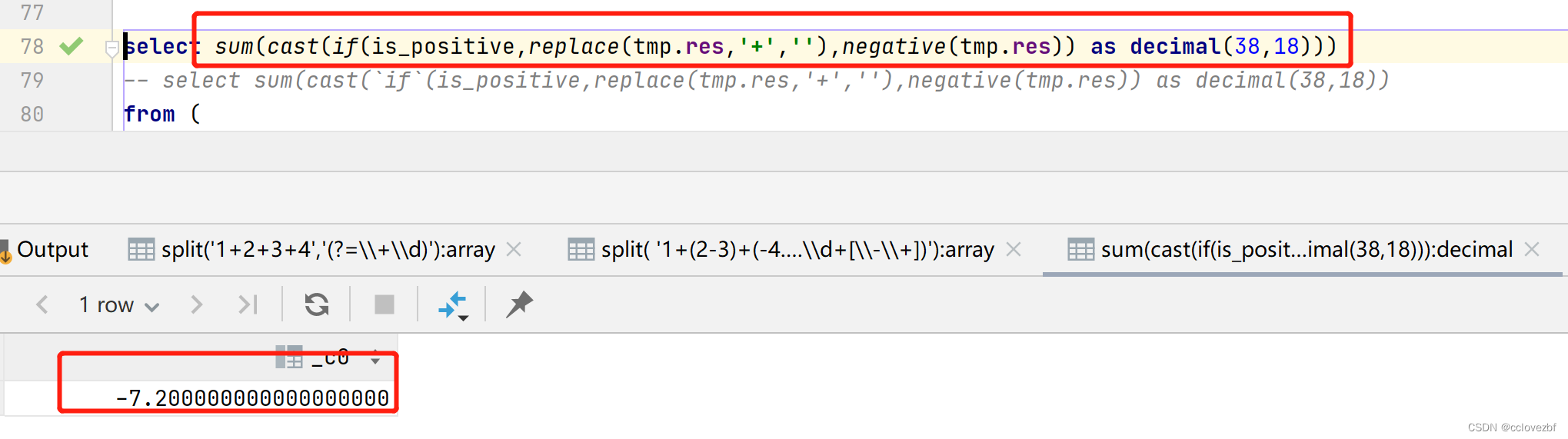
select sum(`if`(is_positive,replace(tmp.res,'+',''),negative(tmp.res)))
from (
select t.a,
substr(t.a, instr(t.a, '(') + 1, `if`(t.a not like '%(%',
length(t.a),
instr(t.a, ')') - instr(t.a, '(') - 1
)) res,
instr(t.a, ')'),
instr(t.a, '('),
is_positive
from (
select t.a a, `if`(substr(a, 1, 1) = '-' and locate('(',a)>0, false, true) is_positive
from (select explode(split('1+(2-3)+(-4.1-3.1)+13-(4-3)-(-3.3+4.3)-11',
'(?=([\\-\\+]\\())|(?=[\\-\\+]\\d+($|[\\+\\-]))')) a) t
) t
)t lateral view explode(split(t.res,'(?=[+-]\\d)'))tmp as resselect 1+(2-3)+(-4.1-3.1)+13-(4-3)-(-3.3+4.3)-11
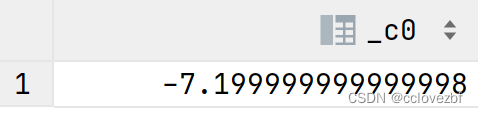
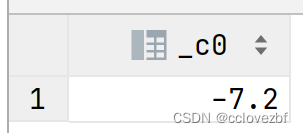
结果有点误差因为是string是看作float去计算的 所以有误差,cast as decimal就好了