1   算法介绍

  冒泡排序法又叫起泡法，在许多程序设计中，我们需要将一个数列进行排序，以方便统计，常见的排序方法有冒泡排序，二叉树排序，选择排序等等。而冒泡排序一直由于其简洁的思想方法和比较高的效率而倍受青睐。

2   算法目的

   按要求对一组元素从大到小或从小到大排序。

3   基本思想

   对未进行排序的元素从头到尾依次比较相邻的两个元素是否逆序（与指定顺序相反），若逆序，则交换这两个元素的位置，这样经过一轮比较过后便可把最大（或最小）的元素排好。然后按照同样的方法对剩下的元素进行比较，直到所有元素都按要求的顺序排列为止，这样就得到了想要的序列。

4   定量分析

   假设共有n（n>=2）个元素需要进行排序，我们把从头到尾的一次比较过程叫着一轮排序，每一轮排序只能将一个元素排好，因此需要进行n-1轮排序才能将n个元素都排好（最后一轮排序只有一个元素，因此无需再进行这一轮排序）。

   因为每一轮排序只能排好一个元素，所以第i轮排序过后便会有i个元素被排好，n-i个元素还未排好，被排好的元素是第n-i+1个。在第i轮的排序过程中，会进行（n-i+1）-1次比较。

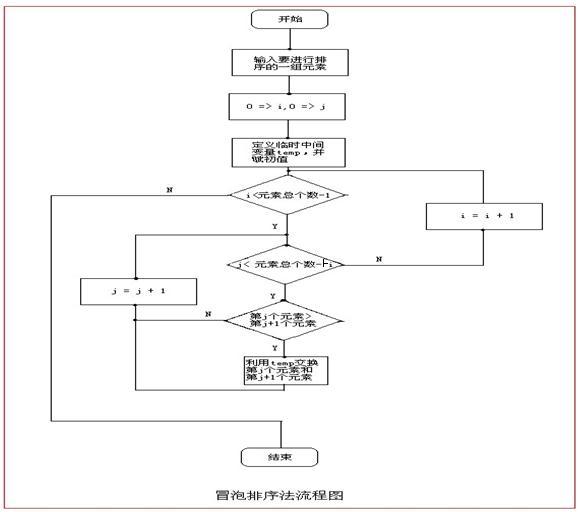
5   算法流程图

6   算法分析

6.1 算法的时间复杂度

  算法的最好时间复杂度

  若文件的初始状态是正序的，一趟扫描即可完成排序。所需的关键字比较次数C和记录移动次数M均达到最小值：

   Cmin=n-1

   Mmin=0

  冒泡排序最好的时间复杂度为O(n)。

  算法的最坏时间复杂度

  若初始文件是反序的，则需要进行n-1趟排序。每趟排序要进行n-i次关键字的比较(1≤i≤n-1)，且每次比较都必须移动记录三次来达到交换记录位置。在这种情况下，比较和移动次数均达到最大值：

  Cmax=n(n-1)/2=O(n²)

  Mmax=3n(n-1)/2=O(n²)

 冒泡排序的最坏时间复杂度为O(n²)。

  算法的平均时间复杂度为O(n²)

6.2 算法的空间复杂度

 冒泡算法的辅助空间复杂度是O(1)。

6.3 算法稳定性

 冒泡排序是就地排序，且它是稳定的。

7   算法实现

7.1  C实现

#include "stdio.h" main() { int a[10]; int i,j,temp; printf("-----输入要排序的十个数字-----"); for(i = 0;i < 10; i++) { scanf("%d",&a[i]); } printf("-----排序前-----"); for(i = 0;i < 10; i++) { printf("%d/r/n",a[i]); } for(i = 0,temp = 0; i < 10 - 1; i++) { for(j = 0; j < 10 - i; j++) { if(a[j] > a[j+1]) { temp = a[j]; a[j] = a[j+1]; a[j+1] = temp; } } } printf("-----排序后-----"); for(i = 0; i< 10; i++) { printf("%d/r/n",a[i]); } }

7.2  C#实现

static void Main(string[] args) { int[] a = new int[10] { 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 }; int i = 0, j = 0, temp; Console.WriteLine("输入要排序的十个整数"); for (i = 0; i < 10; i++) { a[i] = int.Parse(Console.ReadLine()); } Console.WriteLine("------排序前-------"); for (i = 0; i < a.Length; i++) { Console.WriteLine(a[i]); } for (i = 0; i < a.Length - 1; i++) { for (j = 0; j < a.Length - i - 1; j++) { if (a[j] > a[j + 1]) { temp = a[j]; a[j] = a[j + 1]; a[j + 1] = temp; } } } Console.WriteLine("------排序后--------"); for (i = 0; i < a.Length; i++) { Console.WriteLine(a[i]); } Console.Read(); }

7.3  C++实现

#include <iostream> using namespace std; void main() { int a[10]={1,45,89,63,21,47,89,58,85,32},n=9; cout<<"输入的数组元素如下："<<endl; for(int k=0;k<=n;k++) { cout<<a[k]<<" "; } for ( int i = 0,temp = 0;i < n;i++) { for(int j = 0;j < n-i;j++) { if(a[j] > a[j+1]) { temp = a[j]; a[j] = a[j+1]; a[j+1] = temp; } } } cout<<endl<<"排序后的数组元素如下："<<endl; for(int k=0;k<=n;k++) { cout<<a[k]<<" "; } cout<<endl; cin>>n; }

7.4  JAVA实现

public class Bubblesort { public static void main(String[] args) { int[] a = new int[] { 10, 23, 44, 33, 25, 543, 53, 543, 56, 55 }; System.out.println("数组排序前的状态"); for (int k = 0; k < a.length; k++) { System.out.print(a[k] + " "); } for (int i = 0, temp; i < a.length - 1; i++) { for (int j = 0; j < a.length - 1 - i; j++) { if (a[j] > a[j + 1]) { temp = a[j]; a[j] = a[j + 1]; a[j + 1] = temp; } } } System.out.println("数组排序后的状态"); for (int k = 0; k < a.length; k++) { System.out.print(a[k] + " "); } } }

谢谢你的鼓励和支持！