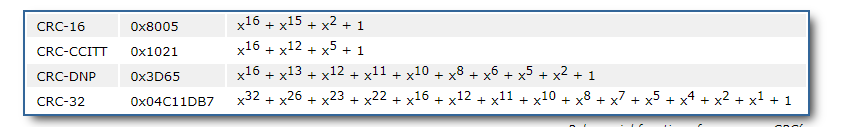循环冗余校验(Cyclic Redundancy Check, CRC)
原理:先在要发送的帧后面附加一个二进制数,(用来校验的校验码);生成一个新帧发送给接收端
附加的二进制数要求:使所生成的新帧能与发送端和接收端共同选定的某个特定数整除
运算:这里的除是指“模2除法”
过程:到达接收端后,把接收到的新帧除以选定的除数
因为在发送端发送数据帧之前加了一个数,做了“去余”处理,所以结果应该没有余数
如果有余数,代表出现错误
模2加法:1+1=(1)0 ;0+1=1;0+0=0 —— 满2进1,保留当前位
模2减法:0-1=1;1-1=0;1-0=1;0-0=0 —— 借1当2,保留当前位
约等于异或
模2乘法:不进位
例子:
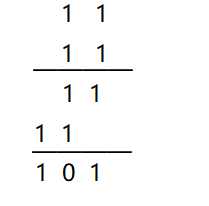
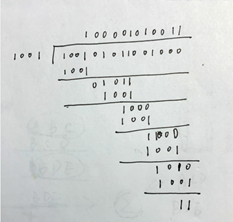
模2除法:在求余数时用模2减
例子:
步骤
• 选择除数,即一个二进制比特串或者多项式
• 得到CRC校验码,即FCS(帧校验序列)
• 组装新帧,发送给接受端;接收端 模2除,没有余数则无差错
• 图示:

多项式除数转换:

注意:余数的位数只能比除数得位数少一位,否则前面补零;FSC规定最高位最低位必须为1
计算题:
1.(搜狗百科例题) 被校验的数据M(x)=1000,选择生成多项式为G(x)=x3+x+1,问,循环冗余校验码时多少?
答:G(x)=x3+x+1对应二进制数为1011;四位
得余数:1000000 B 除 1011B–>余数得101B,即校验码为101B;
(B代表二进制)
所以循环冗余校验码为:1000101B
(验证:1000101B 除 1011B–> 余数 = 0)
2. 假设CRC生成多项式为G(X)=X4+X3+1,求二进制序列10110011得CRC校验码?
答:G(X)=X4+X3+1对应二进制数为11001
101100110000B 除 11001B 得余数 0100B
所以:101100110100B
3. (牛客网)要发送的数据为11001001,采用CRC的生成多项式是P(X)=X3+X+1,则应添加在数据后面的余数为?
答:1011;11001001000B除1011B余数得001B
参考文档:
1、通俗易懂的CRC校验
2、[搜狗百科]模2除法
如有错误,欢迎指正!