目录
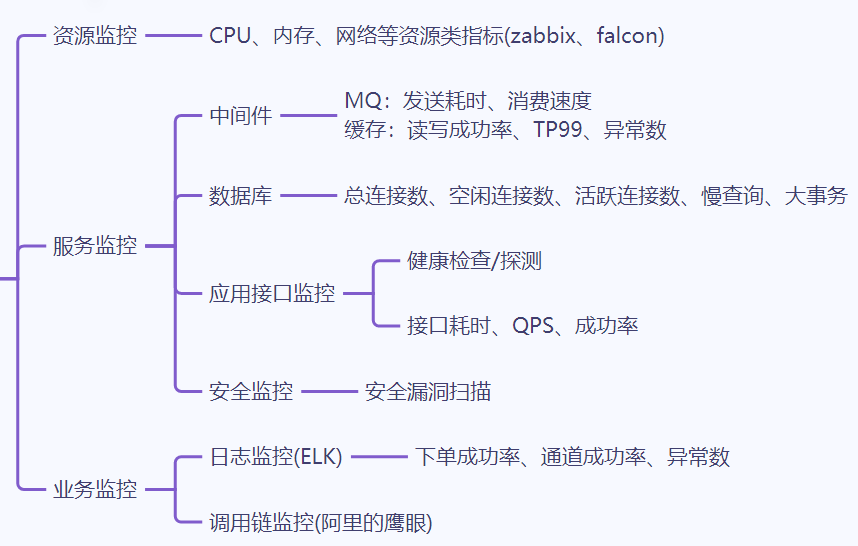
知识结构
编辑内容精读
1.时间序列及其分开类
2.描述性分析
3.时间序列预测
3.1预测过程
3.2平稳时间序列
3.3趋势型序列
3.4复合型序列
名词解释
知识结构
 内容精读
内容精读
1.时间序列及其分开类
时间序列顾名思义就是按时间顺序观察排列而成的序列,根据观察时间的不同,时间序列的时间可以是年份、季度、月份等。根据观测值的分布情况时间序列可以分为平稳序列和非平稳序列:
- 平稳序列就是观察值在某一固定水平上下波动,这种波动的程度可能不同但不存在明显的规律,也就可以看成是随机的。
- 非平稳序列是包含趋势、季节性、周期性的序列,他可能只含有一种成分,也可能含有多种。
于是时间序列的成分便可以分为随机性波动(I)、趋势(T)、季节性(S)、周期性(C)。传统时间序列分析的一项主要内容就是把这些成分从时间序列中分离出来。按照乘法模型,它的形式为:
$$Y_{t}=T_{t}*S_{t}*C_{t}*I_{t}$$
2.描述性分析
(1)图形分析

上图中从左上到左下依次为平稳时间序列、有趋势的时间序列、有季节性的时间序列、即有趋势又有季节性的复合时间序列、有周期性的时间序列。
(2)增长率分析
增长率也就是增长速度,时时间序列中报告期观察值与基期观察值之比减1的结果。增长率又可以分为环比增长率和定基增长率。
环比增长率:$G_{i}=\frac{Y_{i}-Y_{i-1}} {Y_{i-1}}=\frac{Y_{i}} {Y_{i-1}}-1$,说明现象逐期增长的情况。
定基增长率:$G_{i}=\frac{Y_{i}-Y_{0}} {Y_{0}}=\frac{Y_{i}} {Y_{0}}-1$,说明现象在整个观察期内总的增长变化程度。
平均增长率也称平均增长速度,时时间序列中逐期环比值的几何平均数减1的结果,
$$\bar{G}=\sqrt[n]{(\frac{Y_{1}}{Y_{0}})(\frac{Y_{2}}{Y_{1}})…(\frac{Y_{n}}{Y_{n-1}})}-1=\sqrt[n]{\frac{Y_{n}}{Y_{0}}}-1$$
3.时间序列预测
3.1预测过程
(1)确定成分
首先应确定时间序列包含哪些成分,也就是确定类型,再根据类型进行相应的处理。需要注意的是要确定季节性的存在至少需要两年的数据。
(2)选择方法
在明确时间序列的类别后,就要根据类别选择合适的预测方法,预测方法有移动平均、指数平滑、回归模型……具体在后面进行介绍。
(3)预测方法评估
在选定方法后,需要评价该方法的预测效果或准确性。就是找出预测值与实际值的差距,也就是预测误差。常用的预测误差主要有以下几种:
- 平均误差
$$ME=\frac{\sum_{i=1}^{n}(Y_{i}-F_{i})} {n}$$ - 平均绝对误差
$$MAD=\frac{\sum_{i=1}^{n}| Y_{i}-F_{i} |} {n}$$ - 均方误差
$$MSE=\frac{\sum_{i=1}^{n}(Y_{i}-F_{i})^2} {n}$$ - 平均百分比误差
$$MPE=\frac{\sum_{i=1}^{n}(\frac{Y_{i}-F_{i}} {Y_{i}} *100)} {n}$$ - 平均绝对值百分比误差
$$MAPE=\frac{\sum_{i=1}^{n}(\frac{| Y_{i}-F_{i} |} {Y_{i}} *100)} {n}$$
这些误差各有优劣,需要根据具体问题具体分析,主要使用的还是MSE。
3.2平稳时间序列
(1)简单平均法
简单平均法就是根据已有的t期观察值,通过简单平均来预测下一期的数值。比如已有t期的数据,则第t+1期的观察值为:
$$F_{t+1}=\frac{1}{t}(Y_{1}+Y_{2}+…+Y_{t})=\frac{1}{t}\sum_{i=1}^{t}Y_{i}$$
该方法适合较为平稳的序列,且对远期和近期的数值视为同等重要,但从实际预测角度来看,近期的数值比远期对未来有更大的作用。
(2)移动平均法
移动平均法是通过对时间序列筑起递移求得平均数作为预测值的一种方法,有简单移动平均法和加权移动平均法两种,主要介绍简单移动平均法。
简单移动平均是将最近k期的数据加以平均,作为下一期的平均值:
$$\bar{Y}_{t}=\frac{T_{t-k+1}+Y_{t-k+2}+…+Y_{t-1}+Y_{t}} {k}$$
移动平均法同样适合较平稳的时间序列,在预测时选择不同的移动间隔,得到的结果也是不同的。
(3)指数平滑法
指数平滑法通过对过去的观察值加权平均进行预测,使t+1期的预测值等于t期的观察值与t期的预测值的加权平均值。对于该方法,观察值的时间越远其权数呈现指数下降。指数平滑法又分为一次指数平滑法、二次指数平滑法、三次指数平滑法。主要介绍一次指数平滑。
$$F_{t+1}=\alpha Y_{t}+(1-\alpha)F_{t}$$
由于最开始还没有预测值,因此设$F_{1}=Y_{1}$。
3.3趋势型序列
上面介绍的几种方法都只适用于平稳的序列预测,当序列具有明显的趋势或季节性时,这些方法就不适用了。
(1)线性趋势预测
当现象按照线性趋势发展变化时,可以采用线性方程进行预测:
$$\hat{Y}_{t}=b_{0}+b_{1}t$$
对于这个方程的系数的计算,我们在一元回归中已经做了详细的介绍。
(2)非线性趋势预测
当时间序列呈现出某种非线性的趋势时,就需要拟合合适的趋势曲线。
指数曲线
用于描述几何级数递增或递减的现象。
$$\hat{Y}_{t}=b_{0}b_{1}^t$$
其中$b_{0},b_{1}$为待定系数,若$b_{1}>1$,则增长率随时间增加而增加,若$b_{1}<1$,则增长率随时间增加而降低,若$b_{0}>0,b_{1}<1$,则预测值$\hat{Y}_{t}$逐渐降低到以0为限。
$b_{0},b_{1}$的计算方式如下:
3.4复合型序列
当时间序列包含趋势、季节、周期和随机成分中的多个时,就需要将这些因素先依次分解出来,再进行预测。 在现实中我们遇见最多的是$Y_{t}=T_{t}*S_{t}*I_{t}$这一模型,即包含趋势、季节性和随机成分的序列。因为对于周期成分的分析需要多年的数据,而现实很难收集到。对于这一模型主要的预测方法有季节性多元回归模型、季节自回归模型、时间序列分解法预测等。这里主要介绍时间序列分解法:
(1)计算季节指数,这里根据移动平均趋势剔除法计算季节指数:
- 计算移动平均值,如果是季度数据则采用4项移动平均,月份数据则是12项,并对结果在进行二次移动平均,也叫做中心化处理。
- 计算移动平均值的比值,也叫季节比率。就是各观察值除以第一步得到的相应的中心化移动平均值,然后计算各比值的季度(月度)平均值。
- 季节指数调整。若第二步得到的季节指数平均数之和不等于1,则将每个季节指数平均数除以总平均值。
(2)分离季节成分
计算出季节成分之后,就要将各观察值分别除以相应的季节指数,将季节成分分离出去:
$$\frac{Y} {S}=\frac{T*S*I} {S}=T*I$$
ps:剔除季节性后预测的结果是不考虑季节性影响的,若要包含季节因素只需要乘以相应的季节指数。
名词解释
趋势性(T):趋势性是指时间序列在长期内呈现出来的某种持续上升或持续下降的变动,也称长期趋势。时间序列中的趋势可以是线性的,也可以是非线性的。
季节性(S):季节性也称季节变动,时间序列在一年内重复出现的周期性波动。比如商业活动中,常常听到“销售旺季"或“销售淡季"这类术语。
周期性(C):周期性也称循环波动,时间序列中呈现出围绕长期趋势的一种波浪形或振荡式变动,通常由经济环境的变化引起。其特点为波动周期往往大于1年。动系新
随机性(I):随机性也称不规则波动,时间序列中除去趋势、周期性和季节性之后的偶然性波动。
简单平均法:简单平均法是根据过去已有的t期观察值来预测下一期的数值。其特点为:①简单平均法适合对较为平稳的时间序列进行预测;②将远期的数值和近期的数值看作对未来同等重要,从预测角度看,近期的数值要比远期的数值对未来有更大的作用,因此简单预测平均法预测的结果不够准确;③当时间序列有趋势或有季节变动时,该方法的预测不够准确。
移动平均法:移动平均法是通过对时间序列逐期递移求得平均数作为预测值的一种预测方法,其方法有简单移动平均法和加权移动平均法两种。
其特点为:①将每个观察值都给与相同的权数;②只使用最近k期的数据,在每次计算移动平均值时,移动的间隔都为k;③主要适合对较为平稳的序列进行预测;④对于同一个时间序列,采用不同的移动间隔预测的准确性是不同的,可通过试验的办法,选择一个使均方误差达到最小的移动间隔。
指数平滑法:指数平滑法是通过对过去的观察值加权平均进行预测的一种方法,该方法使t+1期的预测值等于t期的实际观察值与t期的预测值的加权平均值,是加权平均的一种特殊形式,观察值时间越远,其权数也跟着呈现指数的下降,因而称为指数平滑;有一次指数平滑、二次指数平滑、三次指数平滑等。
季节指数:季节指数刻画了序列在一个年度内各月或各季度的典型季节特征。在乘法模型中,季节指数是以其平均数等于100%为条件而构成的,它反映了某一月份或季度的数值占全年平均数值的大小。如果现象的发展没有季节变动,则各期的季节指数应等于100%:如果某一月份或季度有明显的季节变化,则各期的季节指数应大于或小于100%。因此,季节变动的程度是根据各季节指数与其平均数( 100%)的偏差程度来测定的。