大家好,我是微学AI,今天给大家介绍一下人工智能算法工程师(中级)课程4-sklearn机器学习之回归问题与代码详解。回归分析是统计学和机器学习中的一种重要方法,用于研究因变量和自变量之间的关系。在机器学习中,回归算法被广泛应用于预测分析、趋势分析等领域。本文将介绍sklearn机器学习库中的一些常用回归算法,包括线性回归、Lasso回归、岭回归、多任务岭回归、核岭回归以及SVM-SVR模型。我们将分别介绍这些算法的数学原理和公式,并配套完整可运行代码。
文章目录
- sklearn机器学习中的回归介绍与代码详解
- 1. 线性回归
- 线性回归的数学原理
- 线性回归的代码实现
- 2. Lasso回归和岭回归
- Lasso回归和岭回归的数学原理
- Lasso回归和岭回归的代码实现
- 3. 多任务岭回归
- 多任务岭回归的数学原理
- 多任务岭回归的代码实现
- 4. 核岭回归
- 核岭回归的数学原理
- 核岭回归的代码实现
- 5. SVM-SVR模型
- SVM-SVR模型的数学原理
- SVM-SVR模型的代码实现
- 总结

sklearn机器学习中的回归介绍与代码详解
1. 线性回归
线性回归是最简单的回归算法,它假设因变量和自变量之间存在线性关系。线性回归的目标是找到一条直线,使得所有数据点到这条直线的距离之和最小。这个目标可以通过最小二乘法来实现。
线性回归的数学原理
线性回归的模型可以表示为:
y = β 0 + β 1 x 1 + β 2 x 2 + ⋯ + β n x n + ε y = \beta_0 + \beta_1x_1 + \beta_2x_2 + \cdots + \beta_nx_n + \varepsilon y=β0+β1x1+β2x2+⋯+βnxn+ε
其中, y y y是因变量, x 1 , x 2 , … , x n x_1, x_2, \ldots, x_n x1,x2,…,xn是自变量, β 0 , β 1 , … , β n \beta_0, \beta_1, \ldots, \beta_n β0,β1,…,βn是模型参数, ε \varepsilon ε是误差项。
最小二乘法的目标是最小化误差平方和:
J ( β ) = ∑ i = 1 m ( y i − y ^ i ) 2 = ∑ i = 1 m ( y i − ( β 0 + β 1 x i 1 + β 2 x i 2 + ⋯ + β n x i n ) ) 2 J(\beta) = \sum_{i=1}^{m}(y_i - \hat{y}_i)^2 = \sum_{i=1}^{m}(y_i - (\beta_0 + \beta_1x_{i1} + \beta_2x_{i2} + \cdots + \beta_nx_{in}))^2 J(β)=i=1∑m(yi−y^i)2=i=1∑m(yi−(β0+β1xi1+β2xi2+⋯+βnxin))2
其中, m m m是样本数量, y i y_i yi是第 i i i个样本的因变量值, y ^ i \hat{y}_i y^i是第 i i i个样本的预测值。
线性回归的代码实现
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
import numpy as np
# 生成模拟数据
np.random.seed(0)
X = np.random.rand(100, 1)
y = 2 * X[:, 0] + 1 + np.random.randn(100) * 0.05
# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
# 创建线性回归模型
model = LinearRegression()
# 训练模型
model.fit(X_train, y_train)
# 预测
y_pred = model.predict(X_test)
# 评估模型
mse = mean_squared_error(y_test, y_pred)
print("Mean squared error: ", mse)
2. Lasso回归和岭回归
Lasso回归和岭回归是两种常用的正则化线性回归算法。它们在普通线性回归的基础上加入了正则化项,以避免过拟合问题。
Lasso回归和岭回归的数学原理
Lasso回归的模型可以表示为:
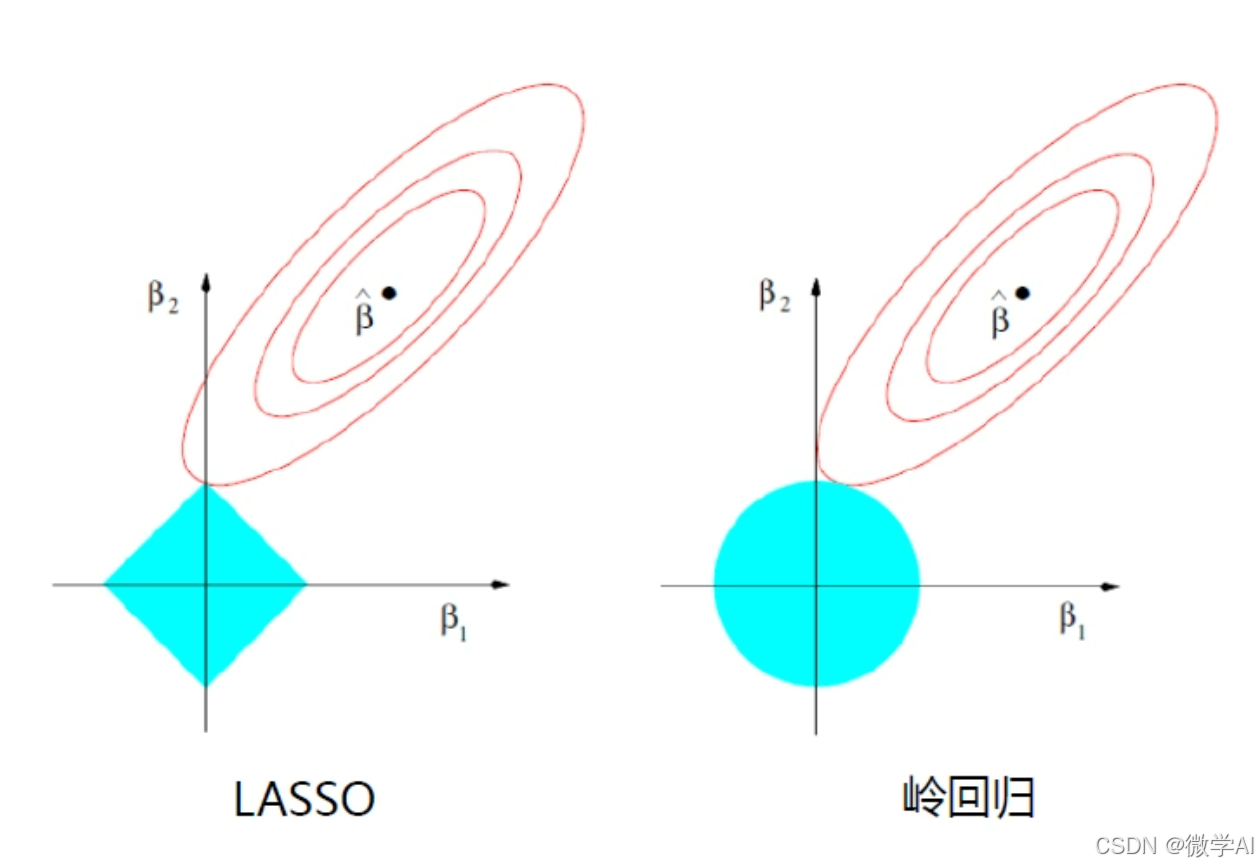
J ( β ) = ∑ i = 1 m ( y i − ( β 0 + β 1 x i 1 + β 2 x i 2 + ⋯ + β n x i n ) ) 2 + α ∑ j = 1 n ∣ β j ∣ J(\beta) = \sum_{i=1}^{m}(y_i - (\beta_0 + \beta_1x_{i1} + \beta_2x_{i2} + \cdots + \beta_nx_{in}))^2 + \alpha \sum_{j=1}^{n}|\beta_j| J(β)=i=1∑m(yi−(β0+β1xi1+β2xi2+⋯+βnxin))2+αj=1∑n∣βj∣
岭回归的模型可以表示为:
J ( β ) = ∑ i = 1 m ( y i − ( β 0 + β 1 x i 1 + β 2 x i 2 + ⋯ + β n x i n ) ) 2 + α ∑ j = 1 n β j 2 J(\beta) = \sum_{i=1}^{m}(y_i - (\beta_0 + \beta_1x_{i1} + \beta_2x_{i2} + \cdots + \beta_nx_{in}))^2 + \alpha \sum_{j=1}^{n}\beta_j^2 J(β)=i=1∑m(yi−(β0+β1xi1+β2xi2+⋯+βnxin))2+αj=1∑nβj2
其中, α \alpha α是正则化参数。
Lasso回归和岭回归的代码实现
from sklearn.linear_model import Lasso, Ridge
# 创建Lasso回归模型
lasso_model = Lasso(alpha=0.1)
# 创建岭回归模型
ridge_model = Ridge(alpha=0.1)
# 训练模型
lasso_model.fit(X_train, y_train)
ridge_model.fit(X_train, y_train)
# 预测
lasso_pred = lasso_model.predict(X_test)
ridge_pred = ridge_model.predict(X_test)
# 评估模型
lasso_mse = mean_squared_error(y_test, lasso_pred)
ridge_mse = mean_squared_error(y_test, ridge_pred)
print("Lasso mean squared error: ", lasso_mse)
print("Ridge mean squared error: ", ridge_mse)
3. 多任务岭回归
多任务岭回归是岭回归的扩展,用于同时解决多个回归问题。这些问题通常是相关的,因此共享相同的特征空间,但有不同的目标值。
多任务岭回归的数学原理
多任务岭回归的目标是最小化以下目标函数:
J ( B ) = 1 2 n ∑ i = 1 n ∥ y i − X i B ∥ 2 2 + α 2 ∑ j = 1 k ∥ B j ∥ 2 2 J(\mathbf{B}) = \frac{1}{2n} \sum_{i=1}^{n} \left\| \mathbf{y}_i - \mathbf{X}_i \mathbf{B} \right\|^2_2 + \frac{\alpha}{2} \sum_{j=1}^{k} \left\| \mathbf{B}_j \right\|^2_2 J(B)=2n1i=1∑n∥yi−XiB∥22+2αj=1∑k∥Bj∥22
其中, B \mathbf{B} B是一个 p × k p \times k p×k的系数矩阵, p p p是特征数量, k k k是任务数量, y i \mathbf{y}_i yi是第 i i i个任务的因变量向量, X i \mathbf{X}_i Xi是第 i i i个任务的自变量矩阵, α \alpha α是正则化参数。
多任务岭回归的代码实现
from sklearn.linear_model import MultiTaskLasso
# 假设我们有两个任务回归任务
X = np.random.rand(100, 10)
y = np.random.rand(100, 2)
# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
# 创建多任务岭回归模型
multi_task_lasso = MultiTaskLasso(alpha=0.1)
# 训练模型
multi_task_lasso.fit(X_train, y_train)
# 预测
multi_task_pred = multi_task_lasso.predict(X_test)
# 评估模型
multi_task_mse = mean_squared_error(y_test, multi_task_pred)
print("Multi Task Lasso mean squared error: ", multi_task_mse)
4. 核岭回归
核岭回归是非线性回归方法,它使用核技巧将数据映射到高维空间,然后维空间中进行线性回归。
核岭回归的数学原理
核岭回归的目标函数为表示为:
J ( w ) = 1 2 n ∥ K w − y ∥ 2 2 + α 2 w T w J(\mathbf{w}) = \frac{1}{2n} \left\| \mathbf{K} \mathbf{w} - \mathbf{y} \right\|^2_2 + \frac{\alpha}{2} \mathbf{w}^T \mathbf{w} J(w)=2n1∥Kw−y∥22+2αwTw
其中, K \mathbf{K} K是核矩阵, w \mathbf{w} w是权重向量, y \mathbf{y} y是因变量向量, α \alpha α是正则化参数。
核岭回归的代码实现
from sklearn.kernel_ridge import KernelRidge
# 创建核岭回归模型
kernel_ridge = KernelRidge(kernel='rbf', alpha=1.0)
# 训练模型
kernel_ridge.fit(X_train, y_train.ravel())
# 预测
kernel_ridge_pred = kernel_ridge.predict(X_test)
# 评估模型
kernel_ridge_mse = mean_squared_error(y_test, kernel_ridge_pred)
print("Kernel Ridge mean squared error: ", kernel_ridge_mse)
5. SVM-SVR模型
支持向量回归(SVR)是支持向量机(SVM)在回归问题上的应用。SVR的目标是找到一个最优的超平面,使得所有数据点到这个超平面的距离之和最小。
SVM-SVR模型的数学原理
SVR的目标函数可以表示为:
min w , b , ξ , ξ ∗ 1 2 ∥ w ∥ 2 + C ∑ i = 1 n ( ξ i + ξ i ∗ ) \min_{\mathbf{w}, b, \xi, \xi^*} \frac{1}{2} \left\| \mathbf{w} \right\|^2 + C \sum_{i=1}^{n} (\xi_i + \xi_i^*) w,b,ξ,ξ∗min21∥w∥2+Ci=1∑n(ξi+ξi∗)
约束条件为:
y i − w T ϕ ( x i ) − b ≤ ε + ξ i w T ϕ ( x i ) + b − y i ≤ ε + ξ i ∗ ξ i , ξ i ∗ ≥ 0 \begin{align*} y_i - \mathbf{w}^T \phi(\mathbf{x}_i) - b &\leq \varepsilon + \xi_i \\ \mathbf{w}^T \phi(\mathbf{x}_i) + b - y_i &\leq \varepsilon + \xi_i^* \\ \xi_i, \xi_i^* &\geq 0 \end{align*} yi−wTϕ(xi)−bwTϕ(xi)+b−yiξi,ξi∗≤ε+ξi≤ε+ξi∗≥0
其中, w \mathbf{w} w是权重向量, b b b是偏置项, ϕ ( x i ) \phi(\mathbf{x}_i) ϕ(xi)是将输入向量映射到高维空间的函数, ξ \xi ξ和 ξ ∗ \xi^* ξ∗是松弛变量, C C C是惩罚参数, ε \varepsilon ε是容忍误差。
SVM-SVR模型的代码实现
from sklearn.svm import SVR
# 创建SVR模型
svr = SVR(kernel='rbf', C=1.0, epsilon=0.1)
# 训练模型
svr.fit(X_train, y_train.ravel())
# 预测
svr_pred = svr.predict(X_test)
# 评估模型
svr_mse = mean_squared_error(y_test, svr_pred)
print("SVR mean squared error: ", svr_mse)
总结
本文给大家展示了线性回归、Lasso回归、岭回归、多任务岭回归、核岭回归以及SVM-SVR模型在sklearn库中的实现。每个模型都包括了模型的创建、训练、预测和评估过程。在实际应用中,您需要根据具体问题选择合适的模型,并通过调整模型参数来优化模型性能。
sklearn库为各种回归算法提供了方便的接口,使得在Python中进行回归分析变得简单高效。通过理解和实践这些算法,您可以更好地解决实际问题,并在机器学习领域取得更好的成果。

![[Linux安全运维] Linux用户以及权限管理](https://img-blog.csdnimg.cn/direct/3be28ba78f3c4a7293eaeb71dc53aa7a.png#pic_center)



![[leetcode]minimum-cost-to-reach-destination-in-time 规定时间内到达终点的最小费用](https://i-blog.csdnimg.cn/direct/1c0613d540824a82bd09728d28dfbde0.png)