“在已有的成熟稳定的滤波器基础上，根据业务需要对原设计进行优化调整以得到新的滤波器” 是滤波器设计的一种常用方法。
MIC用有源带通滤波器
介绍一种简单直观的带通滤波器以及计算过程，以作未来可参考的基线设计。该滤波器可用于音频信号（从MIC原始输出）的放大和处理。
符号定义：
Vin —— 麦克风输出原始信号幅值（Vpeak or Vrms）
Vout —— 滤波器输出信号（Vpeak or Vrms）
Ri —— 麦克风内阻，也可以是人为串联的输入电阻
Ro —— 滤波器输出负载，既下一级电路的输入电阻
Kp —— 滤波器通带内目标增益
ωpl —— 滤波器通带低频截止频率，在该频点滤波器增益降低设计目标下限△Kpl
ωph —— 滤波器通带高频截止频率，在该频点滤波器增益降低设计目标下限△Kph
ωcl —— 滤波器低频-3dB截止频率（高通滤波器极点频率）
ωch —— 滤波器高频-3dB截止频率（低通滤波器极点频率）
A(ω) —— 滤波器在ω频点上的增益
设计目标：
| Vin | Vout | Ri | Ro | ωpl | A(ωpl) | ωph | A(ωph) |
| 1V | 34V | 2.2Kohm | 10Kohm | 20Hz*2π | Kp-0.5dB | 20KHz*2π | Kp-0.1dB |
设计步骤：
- 根据目标输出Vout要求计算Kp
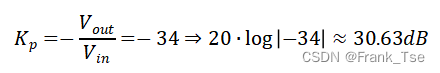
- 根据Kp计算反馈电阻Rf
该构型下放大器的增益
，已知Ri=2.2KΩ，故Rf=75KΩ
- 使用低通滤波器设计式（巴特沃斯逼近）计算高边截止频率ωch（高频极点）
一阶低通滤波器设计式如下
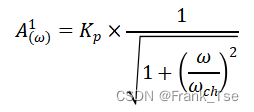
该滤波器中仅有1个由Rf Cf负反馈构成的一阶低通网络，故n取1。同时希望在ωph = 20KHz*2π 频点上将增益波动控制在-0.1dB，即令
，代入设计式可得
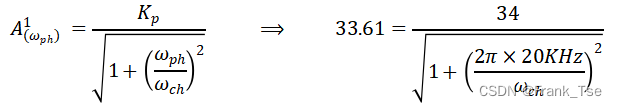
推导可得Rf*Cf负反馈构成的一阶低通网络所需的截止频率（高频极点）ωch
- 使用高边截止频率ωch（极点）计算反馈电容Cf
因截止频率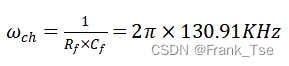
，而Rf已设计为75KΩ，故可得
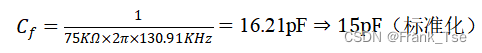
- 使用高通滤波器设计式（巴特沃斯逼近）计算低边截止频率（低频极点）ωcl
高通滤波器设计式如下，其中n为滤波器阶数：
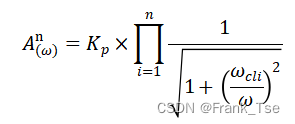
该滤波器中有由Ri*Ci和Ro*Co构成的二阶高通网络，故n取2。同时希望在ωpl = 2π*20Hz频点上将增益波动控制在-0.5dB，即令
，代入设计式可得
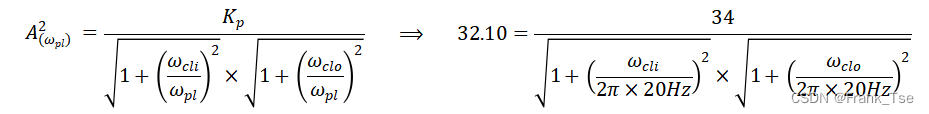
我们希望二阶滤波器的2个极点重合，以在通带外获得最大的滚降速率，既
，可得
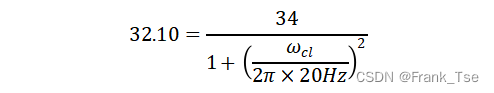
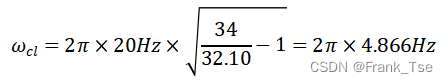
- 使用低边截止频率ωcl（极点）计算反馈电容Ci和Co
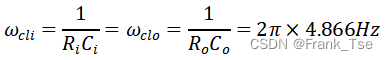
其中Ri和Ro已知，故可得
- 将放大器的直流工作点（偏置电压）设置为VCC中位电压
选择100kΩ 作为Rb1和Rb2的值，直流工作点Vbias = VCC/2
- 设计Cb构成低通滤波器过滤电源引入到Vbias的纹波和噪声
对于交流信号，VCC电源等效与GND短路，故Rb1和Rb2等效为并联，既Rb=50KΩ
设计截止频率为1Hz的低通滤波器，则可得
- 通过TINA-TI仿真检查设计
运放模型需选用理想运放（无限带宽、无限压摆率、无限输出电压、零输出电阻、无限大输入电阻）
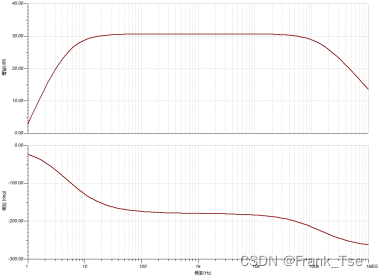
通带内增益30.65dB，20Hz上增益波动-0.494dB，20KHz上增益波动-0.086dB，满足设计要求。
- 加入实际运放模型再次进行仿真，调整RC参数
实际运放存在带宽、输入电阻、输出电阻等限制，而上述计算是假设运放为理想运放获得的结果，因此在使用实际运放搭建电路后其实测结果会偏离设计值。
若可获得实际运放SPICE模型，则最好再使用该运放模型进行仿真，并对相关的RC进行微调。
本案例中加入LM358运放的SPICE模型再次仿真后得到的频响曲线如下
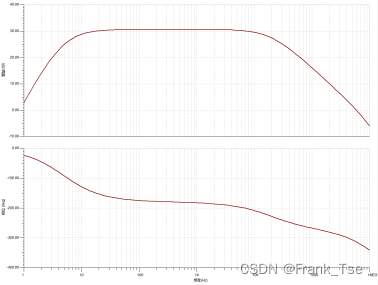
通带内增益30.64dB，20Hz上增益波动-0.483dB，20KHz上增益波动-3.21dB，可见在高频边界上的增益衰减大幅增加，无法满足设计要求！
此时先尝试将Cf Rf设计得更小，企图令滤波器高频截止频率提高，然而仿真发现将Cf直接断开后，在20KHz上的增益波动仍达到了-2.57dB，故可判断是LM358的带宽无法满足本案例的应用需求。
从LM358规格书中得知该运放的增益带宽积GBW=1MHz，而在不同增益下的频响曲线如下
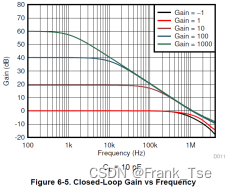
在该应用34倍增益需求下，LM358的理论带宽仅有29KHz，已经非常接近应用所需的20KHz。可见，该设计需要使用带宽性能更高的运放。
最终，选用GBW=6.4MHz的OPA404运放（在34倍增益下理论带宽为188KHz），并将Cf改为4.7pF，仿真结果如下
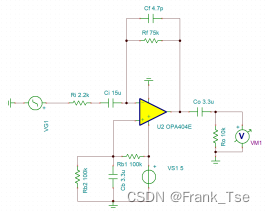
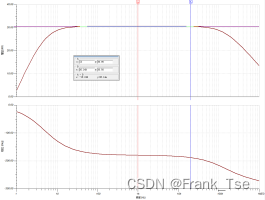
通带内增益30.64dB，20Hz上增益波动-0.494dB，20KHz上增益波动-0.088dB，满足设计要求。
附录：
由n个1阶滤波器构成的n阶低通滤波器设计式
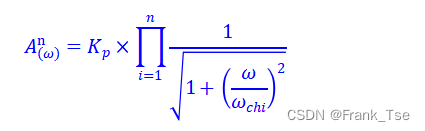
由n个1阶滤波器构成的n阶高通滤波器设计式
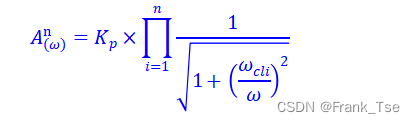
实际上该公式描述的就是伯德图上以【-20n(dB)/十倍频】速度滚降的幅频曲线。
可见随着阶数n提高，所描述曲线的滚降速率会成 -20dB 的倍数增长，如二阶滤波器滚降速率变为 -40dB/十倍频。
