判断一个正整数是否是2的整数次幂(如16是2的4次方,返回true;18不是2的整数次幂,则返回false),要求性能尽可能高。
使用一个整型变量,让它从1开始不断乘以2,将每一次乘2的结果和 目标整数进行比较。
def power2(a):temp=1#循环while temp<=a:#如果相等,就是2的整数次幂if a==temp:return True#每次乘以2# temp*=2#可以修改成,向左移1位temp=temp<<1return Falseif __name__ == '__main__':print(power2(16))print(power2(19))这样确实有一定优化。但目前算法的时间复杂度仍然是O (logn),本质上没有变。
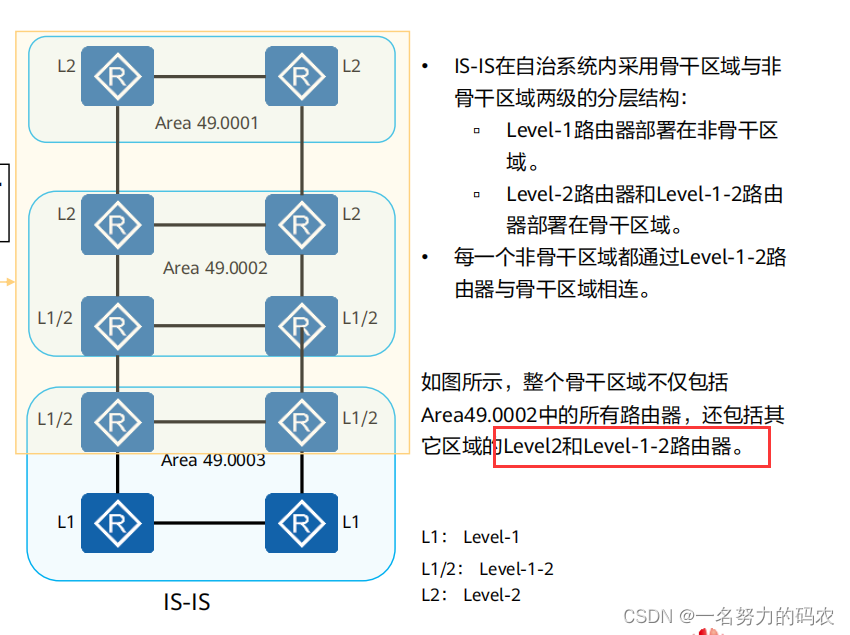
如果把2的整数次幂转换成二进制数,会有什么样的共同点?
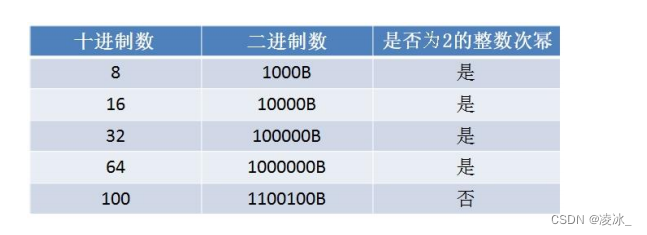
上面都是一个整数是2的整数次幂,当它转化成二进制数时,只有最高位是1,其他位都是0
减1

发现: 2的整数次幂一旦减1,它的二进制数的数字就全部变成了1!
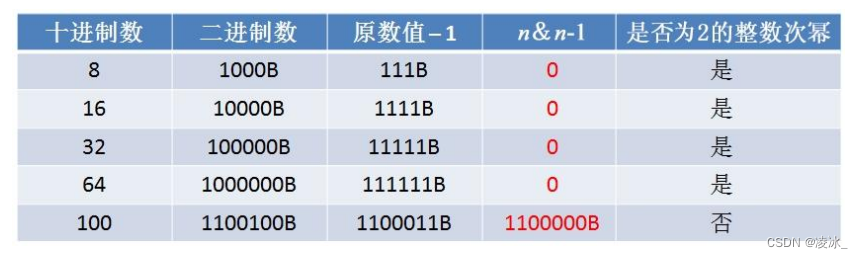
发现: 0和1按位与运算的结果是0,所以凡是2的整数次幂和它本身减1的结果进行与运 算,结果都必定是0。反之,如果一个整数不是2的整数次幂,结果一定不是0
对于一个整数n,只需要计算n& (n-1)的结果是不是0。这个方法的时间复杂度只有O (1)。
def power2_proirity(a):return a &(a-1)==0