论文阅读
https://arxiv.org/pdf/1710.10903
abstract
GAT,作用于图结构数据,采用masked self-attention layers来弥补之前图卷积或类似图卷积方法的缺点。通过堆叠layers,让节点可以添加其邻居的特征,我们就可以给不同的邻居节点不同的权重,而这一步操作不需要使用任何昂贵的矩阵计算(比如求逆矩阵),也不需要依赖对图结构的了解。
可以很容易地应用于inductive,transductive 问题(归纳、直推)。
introduction
CNN:grid-like structure, efficiently reuse their local filters, with learnable parameters, by applying them to all the input positions.
但是很多任务的数据并不能表示成grid-like structure。
->GNN->两种方案:spectral approaches,non-spectral approaches(谱方法、非谱方法)
- spectral approaches
采用图的谱表示方法,已经被成功应用于node classification。依赖于laplacian eigenbasis(拉普拉斯特征基),而laplacian eigenbasis又依赖于图结构,因此在一个图结构上训练的模型并不能直接应用于另一种结构的图。 - non-spectral approaches
定义一个算子,使其能够在不同大小的邻域上工作并且保证CNN的权值共享。
->注意力机制:允许不同大小的输入,专注于输入中最相关的部分来做决策。->通过邻居,找到节点的hidden representation
GAT architecture
graph attentional layer
输入是一系列节点特征:
这里N表示节点的数量,F表示每个节点的特征的数量
而这一层会产生一系列新的节点特征(这里特征的数量可能不同了):
为了获得足够的表达能力将输入的特征转换到更高阶的特征,我们至少需要一个可学习的线性变换->因此出事步骤是一个共享的线性变换,将一个权重矩阵应用于所有的节点。紧接着,我们对节点使用self-attention:
计算注意力系数:
这表明了节点j的特征对节点i的重要程度。->这就允许了每个节点都可以影响其他的节点,从而放弃所有的结构信息。我们通过masked attention(对于节点只计算
,这里
表示节点i在图中的一些邻居->对于对于属于i的邻居的j,只计算ij之间的关系)将其引入图结构。这里邻居指的是节点i的一阶邻居,并且包含了节点i。为了让不同节点之间的系数更好比较,做normalization(归一化)
这里的注意力机制a是一个单层的前馈神经网络,用一个权重向量进行参数化,之后使用LeakyReLU做非线性。->注意力机制的系数可以表示为:
这里T表示转置,||表示连接操作
一旦得到归一化的注意力系数,酒可以用于计算计算与之对应的特征的线性组合。为了能够作为每个节点最终的输出特征(在使用一个潜在的非线性之后):
为了稳定自我注意的学习过程,使用multi-head。K个独立注意机制执行表达式的变换,然后将它们的特征连接起来,得到如下输出特征表示:

这里||表示连接,表示由第k个注意力机制(
)和于输入的线性变换相关的权重矩阵
计算的归一化注意力参数。最后返回的输出
中的每个节点包含
特征(而不是
)。
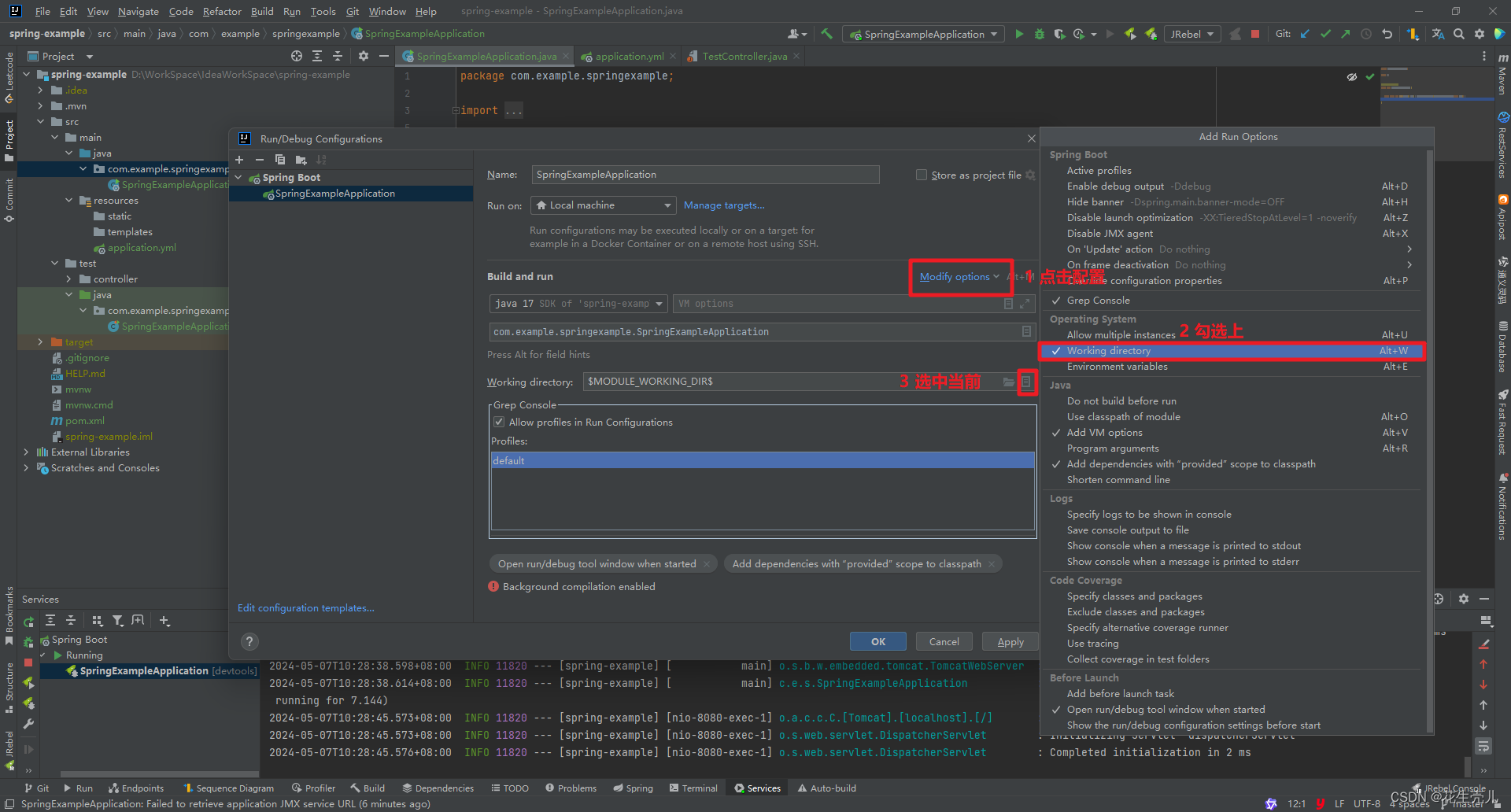
如果我们在网络的最后一层使用multi-head attention,这时,连接就显得不再好用了,这时我们采用的是取平均,并在之后应用非线性:

如上图所示右侧为多头图注意力层(multi-head graph attentional layer)
comparisons to related work
优点
1. 计算高效:self-attention layer上的操作可以在所有边上并行执行,并且对于输出特真多计算可以在节点间并行计算。并且不需要昂贵的特征分解或者类似的昂贵的矩阵计算。
2. 与GCN相比,隐式允许在同一片邻域中赋不同的权重->model capacity↗️↗️
3. 共享。因此,它不依赖于对全局图结构或所有节点(特征)的预先访问(这是许多先前技术的限制)。->不需要图是无向图,并且可以适用于归纳式学习,将模型应用于训练时没有见过的图。
4. 不假设有任何排序
5. 使用节点特征进行相似性计算,而不是节点的结构属性(这将假设预先知道图形结构)。
补充
论文后面的部分就是实验了。
这里摘录一些博客的内容
向往的GAT(图注意力网络的原理、实现及计算复杂度) - 知乎
与GCN的联系与区别
无独有偶,我们可以发现本质上而言:GCN与GAT都是将邻居顶点的特征聚合到中心顶点上(一种aggregate运算),利用graph上的local stationary学习新的顶点特征表达。不同的是GCN利用了拉普拉斯矩阵,GAT利用attention系数。一定程度上而言,GAT会更强,因为 顶点特征之间的相关性被更好地融入到模型中。
为什么GAT适用于有向图?
我认为最根本的原因是GAT的运算方式是逐顶点的运算(node-wise),这一点可从公式(1)—公式(3)中很明显地看出。每一次运算都需要循环遍历图上的所有顶点来完成。逐顶点运算意味着,摆脱了拉普利矩阵的束缚,使得有向图问题迎刃而解。
为什么GAT适用于inductive任务?
GAT中重要的学习参数是与
,因为上述的逐顶点运算方式,这两个参数仅与1.1节阐述的顶点特征相关,与图的结构毫无关系。所以测试任务中改变图的结构,对于GAT影响并不大,只需要改变
,重新计算即可。
与此相反的是,GCN是一种全图的计算方式,一次计算就更新全图的节点特征。学习的参数很大程度与图结构相关,这使得GCN在inductive任务上遇到困境。
下面谈谈我对这一段的理解吧。
首先,第一个GCN和GAT都利用了图的结构关系,区别在于,GCN中节点i的邻域中节点的重要性是图结构确认时就已经定下的,并不是需要学习的参数。在前面的学习中也能看出,一个节点j对节点i越专心,就意味着这个节点天然会分到更大的权重。这一特点同样会影响应用与有向图,假设一个场景,我在微博上关注了一个明星A,并且我很专一,只关注明星A,并且只和明星A互动,如果laplacian,那我就会分到超大的权重,这显然是不合理的。
表示的是节点i的邻域(实际上是节点i的一部分邻居节点),
表示的是一个映射。
我们回顾一下前面的内容
这是在干什么呢?->对于顶点i,计算其邻居与其之间的相似系数

深入理解图注意力机制 - 知乎








![正点原子[第二期]Linux之ARM(MX6U)裸机篇学习笔记-14-主频和时钟配置](https://img-blog.csdnimg.cn/direct/5e42f9ec90ba4351a57deb9dee320b30.png)