目录
- 题目1: 455. 分发饼干
- 1- 思路
- 2- 题解
- ⭐分发饼干 ——题解思路
- 题目2: 摆动序列
- 1- 思路
- 2- 题解
- ⭐摆动序列 ——题解思路
- 题目3: 最大子数组和
- 1- 思路
- 2- 题解
- ⭐ 最大子数组和 ——题解思路
题目1: 455. 分发饼干
- 题目链接:455. 分发饼干
1- 思路
- 贪心的思路,使得饼干和胃口都有序,定义两个指针使得饼干满足孩子胃口进行计数。
2- 题解
⭐分发饼干 ——题解思路

class Solution {public int findContentChildren(int[] g, int[] s) {Arrays.sort(g);Arrays.sort(s);int res = 0;for(int i =0,j=0 ; i<g.length && j<s.length;){if(s[j]>=g[i]){res++;i++;j++;}else{j++;}}return res;}
}
题目2: 摆动序列
- 题目链接:376.摆动序列
1- 思路
- 贪心的思路:局部最优为 删除单调坡 上的元素,只留拐点
- 重点在于摆动的判断:
- ① 单纯峰值:
prediff > 0curdiff <0
- ① 单纯峰值:
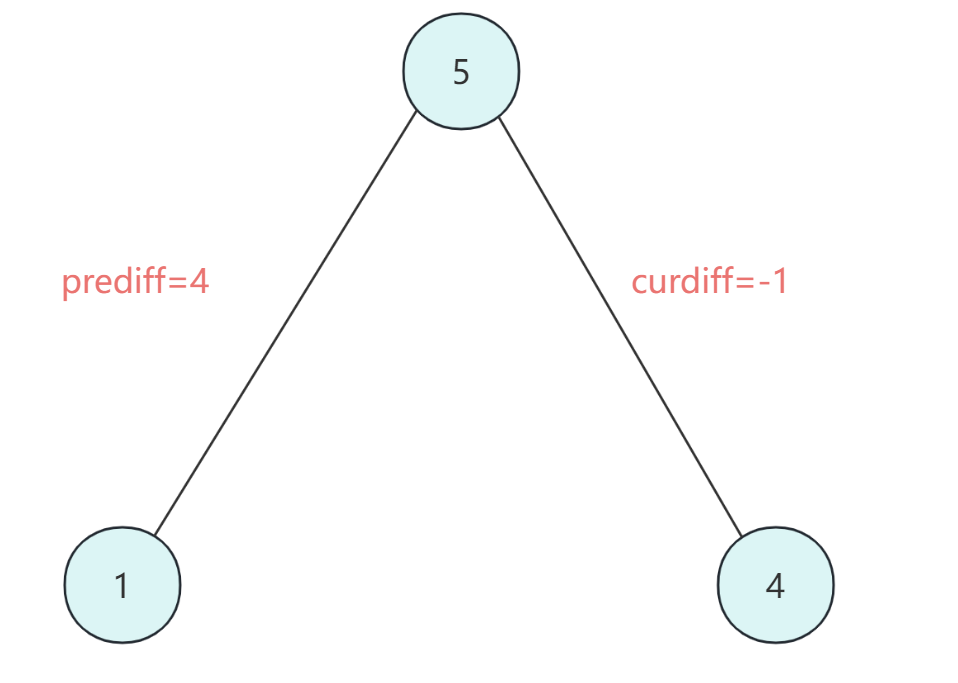
- ② 有平坡:
prediff = 0curdiff <0** **此时也算作摆动
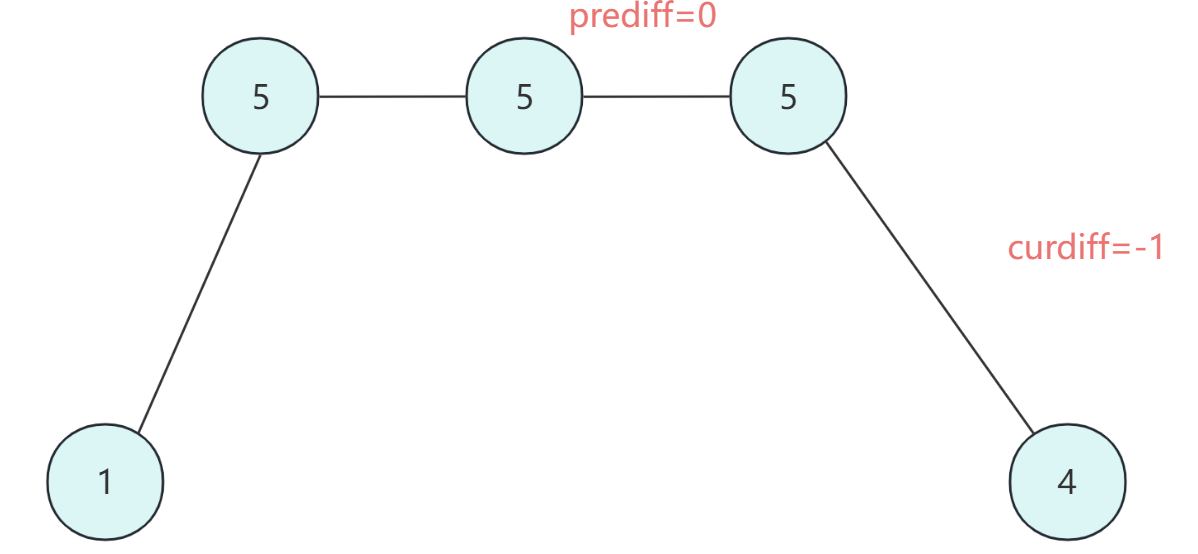
- 借助
prediffcurdiff,其中 prediff 初始化为0,curdiff初始化为1- 此场景是假设 prediff 之前有一个平坡,同时默认序列的最后一个元素是一个摆动
三种结果收集情况
- ①
prediff<=0 && curdiff>0收集结果 ,谷点 - ②
prediff>=0 && curdiff<0收集结果 ,峰点 - ③ 单调有平坡,此时平坡后的一个上升节点不应该统计结果——> 解决办法:不用每次更新
prediff,只在有坡度变化的情况下更新prediff
2- 题解
⭐摆动序列 ——题解思路

class Solution {public int wiggleMaxLength(int[] nums) {int prediff = 0;int curdiff = 0;int res = 1;for(int i = 0 ; i < nums.length-1;i++){curdiff = nums[i+1] - nums[i];if(prediff<=0 && curdiff>0){res++;prediff = curdiff;}else if(prediff >=0 && curdiff<0){res++;prediff = curdiff;}}return res;}
}
题目3: 最大子数组和
- 题目链接:53. 最大子数组和
1- 思路
- 贪心思路,只要当前加了该值,求和结果 > 当前结果 ,即可收集结果
- 如果结果小于 0 ,此时需要重新计算,令
res = 0
2- 题解
⭐ 最大子数组和 ——题解思路

class Solution {public int maxSubArray(int[] nums) {int sum = 0;int res = Integer.MIN_VALUE;for(int i = 0 ; i < nums.length;i++){sum+=nums[i];if(sum>=res){res = sum;}if(sum<0) sum=0;}return res;}
}