详解数据结构：队列（含栈与队列扩展）

一、顺序队列

有一种线性序列，特点是先进先出，这种存储结构称为队列。队列也是一种线性表，只不过它是操作受限的线性表，只能再两端操作：一端进、一端出。进的一端称为队尾，出的一端称为队头。队列可以用顺序存储，也可以使用链式存储。

1、顺序队列的定义

队列的顺序存储采用一段连续的空间存储数据元素，并用两个整型变量记录队头和队尾元素的下标。顺序存储方式的队列如下图：

顺序队列的结构体定义如下：

typedef  struct SqQueue{ElemType *base; //空间基地址int front,rear; //头指针,尾指针
}SqQueue;

说明：

  • ElemType是指元素类型，需要什么类型就写什么类型。
  • typedef将结构体等价于类型名SqQueue。

顺序队列定义好了之后，还要先定义一个最大分配空间，顺序结构都是如此，需要预先分配空间，因此可以采用宏定义。

#define Maxsize 100

上面的结构体定义采用了动态分配的形式，也可以采用静态分配的形式，使用一个定长数组存储数据元素，用两个整型变量记录队头和队尾元素的下标。静态分配的顺序队列结构体定义如下：

typedef  struct SqQueue{ElemType data[Maxszie]; //定长数组int front,rear; //头指针,尾指针
}SqQueue;

注意：队列只能在一端进，一端出，不允许在中间查找、取值、插入、删除等操作，先进先出是人为规定的，如果破坏规则，就不是队列了。

完美图解：

假设现在顺序队列Q分配了6个空间，然后继续入队和出队操作。

注意：Q.front和Q.rear都是整型下标。

（1）开始时为空队，Q.front=Q.rear。如下图

（2）元素a­1入队，放入队尾Q.rear的位置，然后Q.rear后移一位。

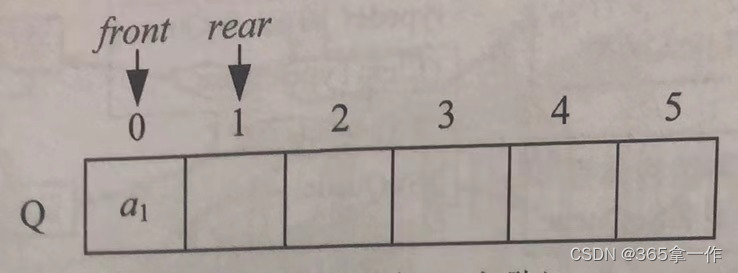
（3）元素a2入队，放入队尾Q.rear的位置，然后Q.rear后移一位。

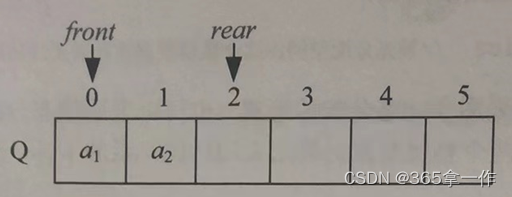
（4）元素a3、a4、a5分别按顺序入队，队尾Q.rear依次后移。

（5）元素a1出队，队头Q.front后移一位。

（6）元素a2­出队，队头Q.front后移一位。

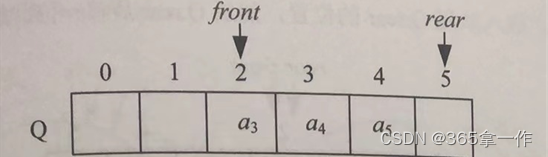
（7）元素a6进队，放在队尾Q.rear的位置，然后Q.rear后移一位。

（8）元素a7­入队，此时队尾Q.rear已经超过了数组的最大下标，无法再进队，但是前面还有两个空间却出现了队满的情况，这种情况称为“假溢出”。

解决方法：上面第七步元素a6进队之后，队尾Q.rear要后移一个位置，此时已经超过了数组的最大下标，即Q.rear+1=Maxsize（最大空间为6），那么如果前面有空闲，Q.rear可以转向前面下标为0的位置。

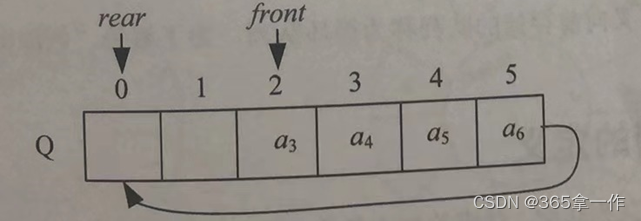
元素a7进队，放入队尾Q.rear的位置，然后Q.rear后移一位。

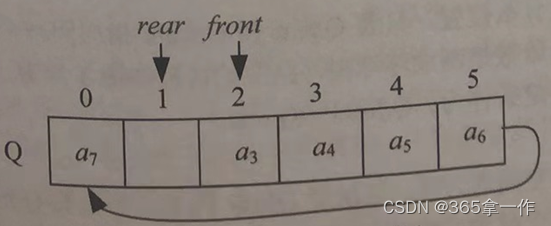
元素a8入队，放入队尾Q.rear的位置，然后Q.rear后移一位。

这时，虽然队列空间存满了，但是出现了一个大问题！当队满了，Q.front=Q.rear，这和队空的条件一模一样，这样无法区分到底是队空还是队满。

解决办法：

  • 设置一个标志，标记队空和队满；
  • 浪费一个空间，当队尾Q.rear的下一个位置是Q.front时，就认为是队满。

上述到达尾部又向前存储的队列称为循环队列，为了避免“假溢出”，顺序队列往2、往采用循环队列。

2、循环队列的定义

首先简述循环队列队空、队满的判定条件，以及出队、队列元素个数计算等基本操作方法。

（1）队空

无论队头和队尾在什么位置，只有Q.rear和Q.front指向同一个位置，就认为队空。如果将循环队列中的一维数组画成环形图，队空的情况如下图：

循环队列空的判定条件为Q.front==Q.rear。

（2）队满

在此采用浪费一个空间的方法，当队尾Q.rear的下一个位置Q.front时，就认为是队满。但是Q.rear向后移动一个位置(Q.rear+1)后，就很有可能超出数组的最大下标，这时它的下一个位置应该是0。

图中，队列的最大空间是Maxsize，当Q,rear=Maxsize-1时，Q.rear+1=Maxszie。而根据循环队列的规则，Q.rear的下一个位置是0。可以考了取余运算，即(Q.rear+1)%Maxsize=0。而此时Q.front=0，即(Q.rear+1)%Maxsize=Q.front，此时为队满的临界状态。

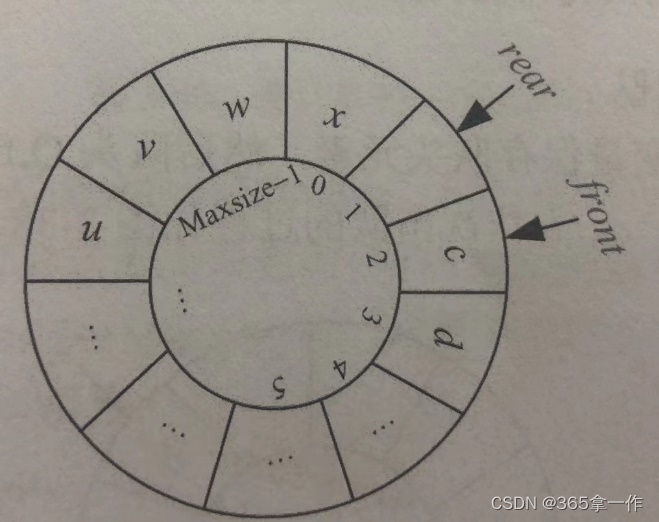
在上图中，加入最大空间数Maxsize=100，当Q.rear=1时，Q.rear+1=2，取余后(Q.rear+1)%Maxsize=2，而此时Q.front=2，即(Q.rear+1)%Maxsize=Q.front。队满的一般状态也可以采用此公式判断队满。因为一个不大于Maxsize的数与Maxisze取余运算，结果仍然为该数本身，所以一般状态下，取余运算没有任何影响。只有在临界状态(Q.rear+1=Maxsize)下，取余运算才会变成0.

因此，循环队列队满的判定条件为：(Q.rear+1)%Maxsize=Q.front

（3）入队

入队时，首先将元素x放入Q.rear所指的空间，然后Q,rear后移一位。

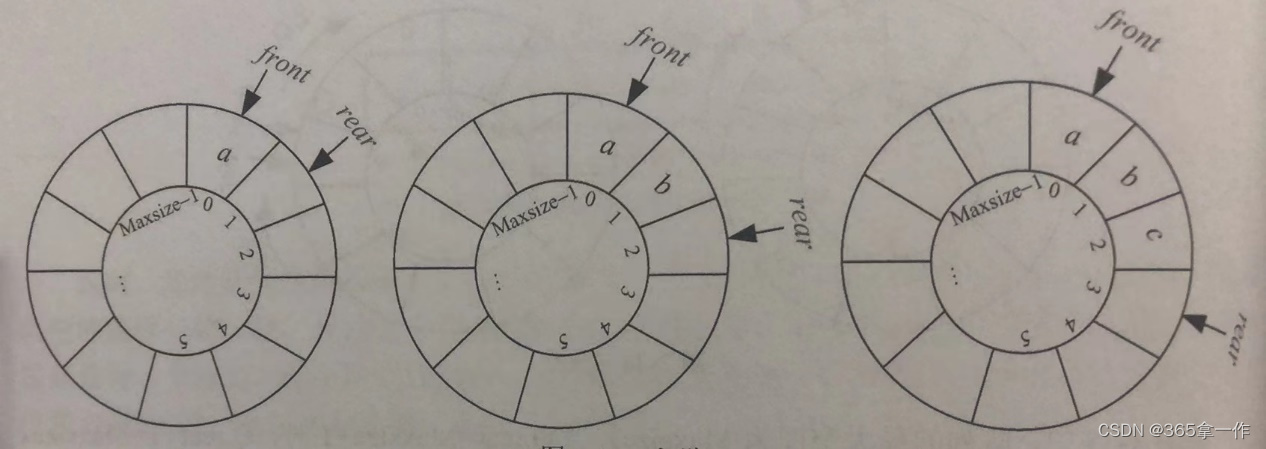
入队操作，当Q.rear后移一位，为了处理临界状态(Q.rear+1)=Maxsize，需要加1后取余运算。

代码实现：

        Q.base[Q.rear]=e; //新元素插入队尾

        Q.rear=(Q.rear+1)%Maxsize; //队尾指针加1

（4）出队

先用变量保存队头元素，然后队头Q.front后移一位。

出队操作，当Q.rear后移一位时，为了处理临界状态(Q.front+1)=Maxsize，需要加1后取余运算。

代码实现：

    e=Q.base[Q.front]; //保存队头元素

    Q.front=(Q.front+1)%Maxsize; //队头指针加1

注意：循环队列无论使出对还是入队，队尾、队头加1后都要取余运算，主要是为了处理临界状态。

（5）队列元素个数计算

循环队列中到底存了多少个元素，循环队列的内容实际上为Q.front~Q.rear-1这一切邮件的数据元素，但是不可以直接用两个下标相减得到。因为队列是循环的，所以存在两种情况：

①Q.rear≥Q.front

②Q.rear<Q.front

可以看到循环队列中的元素实际上为6个，当两者之差是负数的时候，可以将差值加上Maxsize计算元素个数，即Q.rear-Q.front+Maxsize。

因此在计算元素个数时，可以分为两种情况判断：

①Q.rear≥Q.front：元素个数为Q.rear-Q.front

②Q.rear<Q.front：元素个数为Q.rear-Q.front+Maxsize。

也可以采用取余的方法及那个这两种情况巧妙地统一为一个语句。

队列元素的个数为：(Q.rear-Q.front+Maxsize)%Maxsize。

（6）小结

队空：

Q.front==Q.rear;//Q.rear和Q.front指向同一个位置

队满：

(Q.rear+1)%Maxsize==Q.front;//Q.rear向后移一位正好是Q.front

入队：

Q.base[Q.rear]=e; //新元素插入队尾Q.rear=(Q.rear+1)%Maxsize; //队尾指针加1

出队：

e=Q.base[Q.front]; //保存队头元素Q.front=(Q.front+1)%Maxsize; //队头指针加1

队列中元素个数：

(Q.rear-Q.front+Maxsize)%Maxsize。

3、循环队列的基本操作

循环队列的基本包括初始化、入队、出队、取队头元素、求队列长度。

（1）初始化

初始化循环队列，首先分配一个大小为Maxsize的空间，然后令Q.rear=Q.front=0，即队头和队尾为0，队列为空。

代码实现：

bool InitQueue(SqQueue &Q)//注意使用引用参数，否则出了函数，其改变无效
{Q.base=new int[Maxsize];//分配空间if(!Q.base) return false;Q.front=Q.rear=0; //头指针和尾指针置为零，队列为空return true;
}

（2）入队

入队时，首先判断队列是狗已满，如果已满，则入队失败；如果未满，则将新元素插入队尾，队尾后移一位。

代码实现：

bool EnQueue(SqQueue &Q,int e)//将元素e放入Q的队尾
{if((Q.rear+1)%Maxsize==Q.front) //尾指针后移一位等于头指针，表明队满return false;Q.base[Q.rear]=e; //新元素插入队尾Q.rear=(Q.rear+1)%Maxsize; //队尾指针加1return true;
}

（3）出队

出队时，首先判断队列是否为空，如果队列为空，则出队失败；如果队列不空，则用变量保存队头元素，然后队头后移一位。

代码实现：

bool DeQueue(SqQueue &Q, int &e) //删除Q的队头元素，用e返回其值
{if(Q.front==Q.rear)return false; //队空e=Q.base[Q.front]; //保存队头元素Q.front=(Q.front+1)%Maxsize; //队头指针加1return true;
}

 （4）取队头元素

取队头元素时，只要把队头元素数据复制一份即可，并未改变队头位置，因此队列中的内容没有改变。

代码实现：

int GetHead(SqQueue Q)//返回Q的队头元素，不修改队头指针
{if(Q.front!=Q.rear) //队列非空return Q.base[Q.front];return -1;
}

（5）求队列的长度

通过前面的分析，我们已经知道循环队列中的元素个数为：(Q.rear-Q.front+Maxsize)%Maxsize，循环队列中元素个数即为循环队列的元素。

代码实现：

int QueueLength(SqQueue Q)
{return (Q.rear-Q.front+Maxsize)%Maxsize;
}

二、链队列

队列除了用顺序存储，也可以用链式存储。

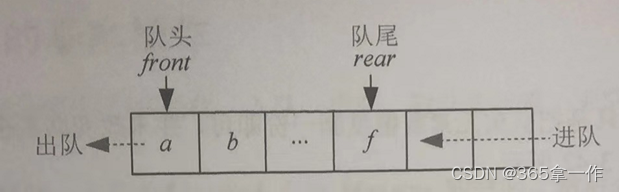
顺序队列是分配一段连续的空间，用两个整型下标front和rear分别指向队头和队尾。而链队列类似一个单链表，需要两个指针front和rear分别指向队头和队尾。从队头出列，从队尾入队，为了出队时删除元素方便，可以增加一个头结点。

注意：链队列需要头结点。

因为链队列是一个单链表的形式，因此可以借助单链表的定义。

链队列中节点的结构体定义如下：

typedef  struct Qnode{int data;struct Qnode *next;
}Qnode,*Qptr;
链队列的结构体定义如下图：
typedef struct{Qnode *front;Qnode *rear;
}LinkQueue;

链队列的操作和单链表一样，只不过他只能队头删除，在队尾插入，是操作受限的单链表。

1、初始化

链队列的初始化，即创建一个头结点，头指针和尾指针指向头结点。

代码实现：

void InitQueue(LinkQueue &Q)//注意使用引用参数，否则出了函数，其改变无效
{Q.front=Q.rear=new Qnode; //创建头结点，头指针和尾指针指向头结点Q.front->next=NULL;
}

2、入队

先创建一个新节点，将元素e存入该节点的数值域。

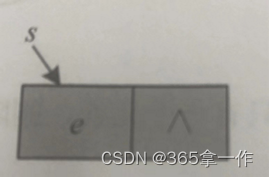
然后将新节点插入队列，尾指针后移。

赋值解释：

①Q.rear->next=s：把s节点的地址赋值给队尾节点的next域，即尾节点的next指针指向s。

②Q.rear=s：把s节点的地址赋值给尾指针，即尾指针指向s，尾指针永远指向队尾。

代码实现：

void EnQueue(LinkQueue &Q,int e)//将元素e放入队尾
{Qptr s;s=new Qnode;s->data=e;s->next=NULL;Q.rear->next=s;//新元素插入队尾Q.rear=s;     //队尾指针后移
}

3、出队

出队相当于删除第一个元素，即将第一个元素节点跳过去。首先用p指针指向第一个数据节点，然后跳过该节点，即Q.front->next=p->next。

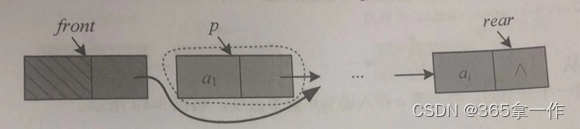
若队列中只有一个元素，删除后需要修改尾指针。

代码实现：

bool DeQueue(LinkQueue &Q,int &e) //删除Q的队头元素，用e返回其值{Qptr p;if(Q.front==Q.rear)//队空return false;p=Q.front->next;e=p->data;     //保存队头元素Q.front->next=p->next;if(Q.rear==p) //若队列中只有一个元素，删除后需要修改队尾指针Q.rear=Q.front;delete p;return true;}

4、取队头元素

队头元素实际上是Q.front->next指向的节点，即第一个数据节点，队头元素就是该节点的数据域存储的元素。

代码实现：

int GetHead(LinkQueue Q)//返回Q的队头元素，不修改队头指针{if (Q.front!=Q.rear) //队列非空return Q.front->next->data;return -1;}

三、栈和队列的应用

1、数制的转换

题目：将一个十进制数n转换为二进制数

解题思路：十进制转换为二进制，可以采用辗转相除法，取余数的方法得到。例如十进制数11转二进制，先求余数11%2=1，求商11/2=5，然后用商5求余数，求商，直到商为0，结束。

先求出的余数是二进制的低位，后求出的余数是二进制的高位，将得到的余数逆序输出就是所要的二进制数，逆序输出正号符合栈的先入后出的性质，因此可以借助栈来实现。

算法步骤：

  1. 初始化一个栈。
  2. 如果n!=0，将n%2入栈，更新n=n/2。
  3. 重复运行第二步，直到n=0为止。
  4. 如果栈不空，弹出栈顶元素e，输出e，知道栈空。

完美图解：

十进制11转换为二进制的计算步骤如下：

  1. 初始化n=11;
  2. n%2=1，1入栈，更新n=11/2=5;
  3. n%2=1，1入栈，更新n=5/2=2;
  4. n%2=0，0入栈，更新n=2/2=1;
  5. n%2=1，1入栈，更新n=1/2=0;
  6. n=0，算法停止。

入栈过程如下图：

如果栈不空，则一直出栈，出栈过程如下：

出栈的结果正好事十进制数11转化为二进制数1011。

代码实现：

void binaryconversion(int n){SqStack S;//定义一个栈Sint e;InitStack(S);//初始化栈while(n){Push(S,n%2);//将n%2压入栈中n=n/2;}while(!Empty(S))//如果栈不空{Pop(S,e);//出栈cout<<e<<"\t";//输出栈顶元素}}

算法复杂度分析：

每次取余后除以2，n除以2多少次变为1那么第一个while语句就执行了多少次，假设执行了x次，则n/2x=1，x=log2n，因此复杂度为为O(log2n)，使用的栈空间大小也是log2n，空间复杂度也是O(log2n)。

2、回文判定

题目：回文是指正反读均相同的字符序列，也就是字符串沿中心线对称。写一算法判定给定的字符串是否为回文。

解题思路：回文是中心对称的，可以将字符串前一半入栈，然后，栈中元素和字符串后一般进行比较。即将第一个出栈元素和后一半中第一个字符比较，如相等，则再将出栈一个元素与后一个字符比较……直到栈空为止，则字符序列为回文。在出栈元素与串中字符比较不等时，则字符序列不是回文。

算法步骤：

  1. 初始化一个栈S。
  2. 求字符串长度，将前面一半的字符串依次入栈S。
  3. 如果栈不空，弹出栈顶元素e，与字符串后一半元素比较。若n为激素，则跳过中心点，比较中心点后面的元素。如果元素相等，则继续比较直到栈空，返回true；如果元素不等，则返回false。

完美图解：

代码实现：

bool palindrome(char *str)//判断字符串是否为回文{SqStack S;//定义一个栈Sint len,i;char e;len=strlen(str);//返回字符串长度InitStack(S);//初始化栈for(i=0;i<len/2;i++)//将字符串前一半依次入栈Push(S,str[i]);if(len%2==1)//字符串长度为奇数，跳过中心点i++;while(!Empty(S))//如果栈不空{Pop(S,e);//出栈if(e!=str[i])//比较元素是否相等return false;elsei++;}return true;}

算法复杂度分析：

如果字符串长度为n，将前一半入栈，后一半依次和出栈元素比较，相当于扫描了整个字符串，因此时间复杂度为O(n)，使用栈空间大小是n/2，空间复杂度也为O(n)。

3、双端队列

题目：设计一个数据结构，使其具有栈和队列两种特性。

解题思路：

栈是后进先出，队列是先进先出。

栈是在一端进出，队列是在一端进、另一端出。

允许两端都可以进行入队和出队的队列，就是双端队列。

双端队列是比较特殊的线性表，具有队列两种性质。

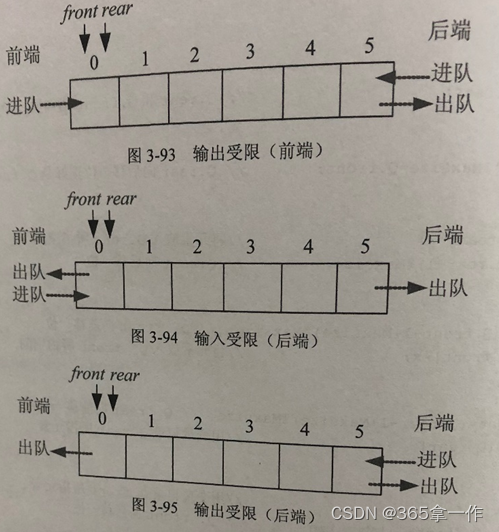
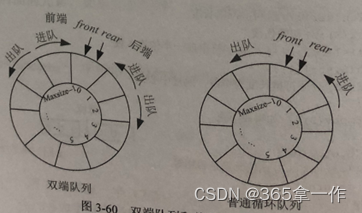
循环队列表示的双端队列，可以用环形形象地表达出来。双端队列和普通循环队列地区别如下图。双端队列包括前端和后端，可以从前端进入、前端出队、后端进队、后端出队。

1、双端队列结构体定义

双端队列可以用两个整型变量front和rear分别指向队头和队尾，采用顺序存储。静态分配空间形式地双端队列，其结构体定义如下：

typedef  struct SqQueue{ElemType base[Maxsize]; //一维数组存储，也可以设置指针动态分配空间int front,rear; //头指针,尾指针}DuQueue;

注意：在顺序存储中，静态分配空间采用的是以为定长数组存储数据，动态分配空间是在程序运行中使用new动态分配空间。

完美图解

（1）前端进队时，先令Q.front前移一位，再将元素放入Q.front的位置，a、b、c依次从前端进队。

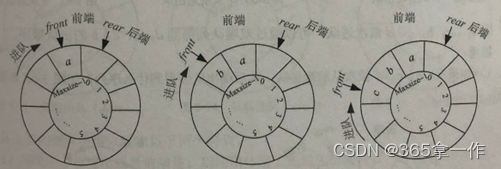
（2）后端进队时，先将元素放入Q.rear的位置，再令Q.rear后移动一位，d从后端进队。

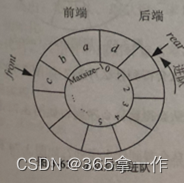
（3）此时d从后端出队，先令Q.rear前移一位，再将Q.rear位置取出。

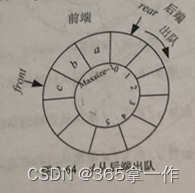
（4）此时a从后端出队，先将Q.rear前移一位，再将Q.rear的元素取出。

（5）此时c从前端出队，先将Q.front位置元素取出，再令Q.front后移一位。

（6）此时b从前端出队，先将Q.front位置元素取出，再令Q.front后移一位。

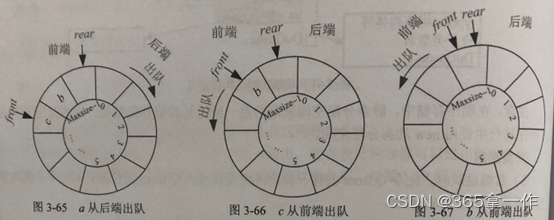
因此，a、b、c、d依次进队，可以通过双端队列得到 d、a、c、b的出队顺序。

从上面的图中可以看出以下两个特点：

  1. 后端进、前端出或者前端进、后端出体现了先进先出的特点，符合队列的特性。
  2. 后端进、后端出或者前端进、前端出提点了后进先出的特点，符合栈的特性。

所以说，循环队列实现的双端队列，具有栈和队列两种性质。

2、双端队列的基本操作

双端队列的基本操作包括初始化、判队满、尾进、尾出、头进、头出、取队头、取队尾、求长度、遍历。

（1）初始化

初始化时，头指针和尾指针为零，双端队列为空。

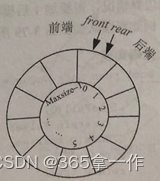
代码实现：

void InitQueue(DuQueue &Q)//注意使用引用参数，否则出了函数，其改变无效{Q.front=Q.rear=0; //头指针和尾指针置为零，队列为空}

（2）判队满

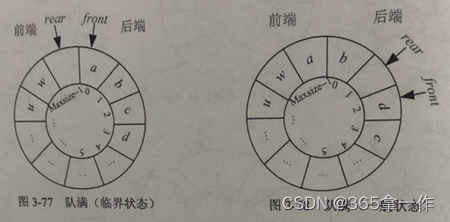
当队尾后移一位等于队头，表明队满，队尾后移一位即Q.rear+1，加1后有可能等于Maxsize，此时下一个位置为0，因此为处理临界状态，需要与Maxsize取余运算。队满的临界状态和一般状态如下图：

代码实现：

bool isFull(DuQueue Q){if((Q.rear+1)%Maxsize==Q.front) //尾指针后移一位等于头指针，表明队满return true;elsereturn false;}

（3）尾进

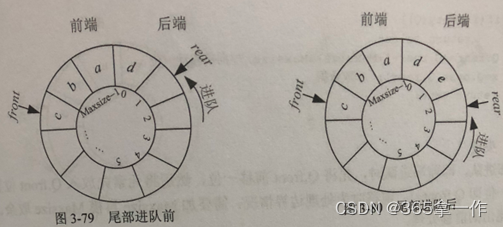
尾部进队，即后端进队时，先将元素放入Q.rear位置，然后Q.rear后移一位，后移时为处理边界情况，需要加1后模Maxsize取余。

代码实现：

bool push_back(DuQueue &Q,ElemType e){if(isFull(Q))return false;Q.base[Q.rear]=e; //先放入Q.rear=(Q.rear+1)%Maxsize;//向后移动一位return true;}

（4）尾出

尾部出队，即后端出队时，先将Q.rear前移一位，然后取出元素。前移一位即Q.rear-1，当Q.rear为0时，Q.rear-1为负值，因此加上Maxsize，正好时Maxsize-1的位置。那么，Q.rear-1为正值时，加上Maxsize就超过了下标范围，需要模Maxsize取余。

尾出时，Q.rear前移一位的处理如下图所示。

代码实现：

bool pop_back(DuQueue &Q,ElemType &x){if(isEmpty(Q))return false;Q.rear=(Q.rear-1+Maxsize)%Maxsize;//向前移动一位x=Q.base[Q.rear]; //取数据return true;}

（5）头进

头部进队时，即前端进队时，先将Q.front前移动一位，然后将元素放入Q.front位置。队头前移一位即Q.front-1，前移时为处理边界情况，需要加Maxsize再模Maxsize取余。和尾出的前移处理一样。

代码实现：

bool push_front(DuQueue &Q,ElemType e){if(isFull(Q))return false;Q.front=(Q.front-1+Maxsize)%Maxsize;//先向前移动一位Q.base[Q.front]=e; //后放入return true;}

（6）头出

头部进队，即前端出队时，先取出元素，然后Q.front后移一位，即Q.front+1，后移时为处理边界情况，需要模Maxsize取余。

代码实现：

bool pop_front(DuQueue &Q,ElemType &x){if(isEmpty(Q))return false;x=Q.base[Q.front]; //取数据Q.front=(Q.front+1)%Maxsize;//向后移动一位return true;}

（7）取队头

取队头是将Q.front位置的元素取出来，Q.front未改变。

代码实现：

bool get_front(DuQueue Q,ElemType &x){if(isEmpty(Q))return false;x=Q.base[Q.front]; //取队头数据;return true;}

（8）取队尾

因为Q.rear指针永远指向空，因此取队尾时，取Q.rear前面的那个位置，要想得到前面位置，为处理边界情况，需要加Maxsize再模Maxsize取余。注意：取队尾时，尾指针不移动。

代码实现：

bool get_back(DuQueue Q,ElemType &x){if(isEmpty(Q))return false;x=Q.base[(Q.rear-1+Maxsize)%Maxsize];return true;}

（9）求长度

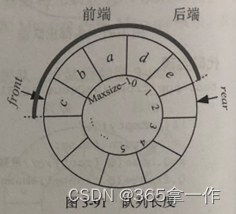
和普通循环队列求长度的方法一样，都是从队头到队尾之间的元素个数。因为循环队列减法有可能有负值，因此需要加入Maxsize再模Maxsize取余。

代码实现：

int length(DuQueue Q){return (Q.rear-Q.front+Maxsize)%Maxsize;}

（10）遍历

双端队列的遍历，即从头到尾输出整个队列的元素，在输出过程中，队头和队尾元素并不移动，因此借助一个暂时变量即可。

代码实现：

void traverse(DuQueue Q){if(isEmpty(Q)){cout<<"DuQueue is empty"<<endl;return ;}int temp=Q.front;//设置一个暂存变量，头指针未移动while(temp!=Q.rear){cout<<Q.base[temp]<<"\t";temp=(temp+1)%Maxsize;}cout<<endl<<"traverse is over!"<<endl;}

此外，还有另外两种方法：

（1)输出受限的双端队列

允许在一端进队和出队，另一端只允许进队，这样的双端队列称为输出受限的双端队列。

（2）输入受限的双端队列

允许在一端进队和出队，另一端只允许出队，这样的双端队列称为输入受限的双端队列。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://xiahunao.cn/news/2980992.html

如若内容造成侵权/违法违规/事实不符，请联系瞎胡闹网进行投诉反馈，一经查实，立即删除！

相关文章

贪心算法在单位时间任务调度问题中的应用

贪心算法在单位时间任务调度问题中的应用

贪心算法在单位时间任务调度问题中的应用 一、引言二、问题描述与算法设计三、算法证明四、算法实现与效率分析五、C语言实现示例六、结论 一、引言 单位时间任务调度问题是一类经典的优化问题&#xff0c;旨在分配任务到不同的时间槽中&#xff0c;使得某种性能指标达到最优。…
阅读更多...
RTU遥测终端为城市排水安全保驾护航！

RTU遥测终端为城市排水安全保驾护航！

近年来&#xff0c;全球气候变迁与城市化进程不断加速&#xff0c;导致强降雨事件频发&#xff0c;道路低洼地带、下穿式立交桥和隧道等区域在暴雨中常易积水&#xff0c;严重阻碍了人民的出行&#xff0c;甚至危及生命与财产安全。而传统的排水管网管理方式已难以适应现代城市…
阅读更多...
elasticsearch-8.1.0安装记录

elasticsearch-8.1.0安装记录

目录 零、版本说明一、安装二、使用客户端访问 零、版本说明 centos [rootnode1 ~]# cat /etc/redhat-release CentOS Linux release 7.9.2009 (Core)elasticsearch elasticsearch-8.1.0-linux-x86_64一、安装 systemctl stop firewalld.servicesystemctl disable firewal…
阅读更多...
MATLAB 数据类型

MATLAB 数据类型

MATLAB 数据类型 MATLAB 不需要任何类型声明或维度语句。每当 MATLAB 遇到一个新的变量名&#xff0c;它就创建变量并分配适当的内存空间。 如果变量已经存在&#xff0c;那么MATLAB将用新内容替换原始内容&#xff0c;并在必要时分配新的存储空间。 例如&#xff0c; Tota…
阅读更多...
【Linux】深入理解Linux文件系统与日志分析

【Linux】深入理解Linux文件系统与日志分析

目录 一、inode与block 1.block与inode概述 2.inode的内容 3.inode号码 4.inode的大小 5.访问文件的简单流程 6.inode的特殊作用 7.通过indoe号删除rm常规方法删除不掉的文件 二、硬链接和软链接 三、恢复误删除的文件 1.恢复EXT类型的文件 示例 2.xfs类型文件备份…
阅读更多...
通信场景：动态调整对象池大小

通信场景：动态调整对象池大小

通信场景&#xff1a;动态调整对象池大小 文章目录 通信场景&#xff1a;动态调整对象池大小前言历史通信量队列长度系统资源响应时间结语 前言 在做通信相关的开发时&#xff0c;使用对象池管理用于存放接收数据的内存块&#xff0c;是一种常见的优化技术。特别是在需要频繁分…
阅读更多...
jvm中的引用类型

jvm中的引用类型

Java中的引用类型 1.强引用 一个对象A被局部变量、静态变量引用了就产生了强引用。因为局部变量、静态变量都是被GC Root对象关联上的&#xff0c;所以被引用的对象A&#xff0c;就在GC Root的引用链上了。只要这一层关系存在&#xff0c;对象A就不会被垃圾回收器回收。所以只要…
阅读更多...
洛基计划project loki加速器推荐 免费低延迟联机加速器分享

洛基计划project loki加速器推荐 免费低延迟联机加速器分享

洛基计划project loki加速器推荐 免费低延迟联机加速器分享 《洛基计划》是一款团队PVP游戏&#xff0c;融合有动作、英雄设计、大逃杀等元素&#xff0c;由前拳头游戏、Bungie和暴雪娱乐员工创立的新工作室Theorycraft Games共同发布。《洛基计划》汇集了一些大型团队PVP游戏…
阅读更多...
原生js实现一个简化版的h函数

原生js实现一个简化版的h函数

原生js实现一个简化版的h函数 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>Document</title&…
阅读更多...
轻量和ECS对比：阿里云轻量应用服务器和云服务器有啥区别？

轻量和ECS对比：阿里云轻量应用服务器和云服务器有啥区别？

阿里云轻量应用服务器和云服务器ECS区别对照表&#xff0c;一看就懂的适用人群、使用场景、优缺点、使用限制、计费方式、网路和镜像系统全方位对比&#xff0c;阿里云服务器网aliyunfuwuqi.com整理ECS和轻量应用服务器区别对照表&#xff0c;可以在阿里云CLUB中心领取 aliyun.…
阅读更多...
HTML5+CSS3小实例：炫彩荧光线条登录框

HTML5+CSS3小实例：炫彩荧光线条登录框

实例：炫彩荧光线条登录框 技术栈：HTML+CSS 效果： 源码： 【HTML】 <!DOCTYPE html> <html lang="zh-CN"><head><meta charset="UTF-8"><meta name="viewport" content="width=device-width, initial-sca…
阅读更多...
OpenTelemetry-2.Go接入Jaeger（grpc，gin-http）

OpenTelemetry-2.Go接入Jaeger（grpc，gin-http）

目录 1.什么是OpenTelemetry 2.搭建jaeger 3.链路追踪 本地调用 远程调用 GRPC proto server端 client端 Gin-HTTP 调用流程 api1 api2 grpc 4.完整代码 1.什么是OpenTelemetry 参考&#xff1a;OpenTelemetry-1.介绍-CSDN博客 2.搭建jaeger 参考&#xff1a;…
阅读更多...
第100+6步 ChatGPT文献复现：ARIMAX预测新冠

第100+6步 ChatGPT文献复现：ARIMAX预测新冠

基于WIN10的64位系统演示 一、写在前面 我们继续来解读ARIMAX模型文章&#xff0c;这一轮带来的是&#xff1a; 《PLoS One》杂志的2022年一篇题目为《A data-driven eXtreme gradient boosting machine learning model to predict COVID-19 transmission with meteorologic…
阅读更多...
Android视角看鸿蒙第十二课-鸿蒙的布局之相对布局RelativeContainer

Android视角看鸿蒙第十二课-鸿蒙的布局之相对布局RelativeContainer

Android视角看鸿蒙第十二课-鸿蒙的布局之相对布局RelativeContainer 导读 相对布局和线性、层叠布局一样都是类似于Android布局的&#xff0c;之前两篇文章已经了解线性、层叠布局的使用方法&#xff0c;这篇文章一起来学习下鸿蒙中的相对布局。 之前的文章中&#xff0c;我偶…
阅读更多...
【驱动】AM437x中出现很多bioset进程，杀不掉，有影响吗？

【驱动】AM437x中出现很多bioset进程，杀不掉，有影响吗？

1、问题描述 查看linux系统进程时，发现很多bioset进程 2、问题分析 1）bioset进程是内核线程 这些bioset进程与Linux内核的块I/O（Block Input/Output）层有关，它们是内核线程，不是用户空间的进程。 Linux的块I/O层负责管理磁盘和其他块设备的数据传输。当系统读写磁盘…
阅读更多...
【python程序打包教程】PyInstaller一键打包Python程序为独立可执行exe文件

【python程序打包教程】PyInstaller一键打包Python程序为独立可执行exe文件

《博主简介》 小伙伴们好&#xff0c;我是阿旭。专注于人工智能、AIGC、python、计算机视觉相关分享研究。 ✌更多学习资源&#xff0c;可关注公-仲-hao:【阿旭算法与机器学习】&#xff0c;共同学习交流~ &#x1f44d;感谢小伙伴们点赞、关注&#xff01; 《------往期经典推…
阅读更多...
AI大模型探索之路-认知篇4：大语言模型预训练基础认知

AI大模型探索之路-认知篇4：大语言模型预训练基础认知

文章目录 前言一、预训练流程分析二、预训练两大挑战三、预训练网络通信四、预训练数据并行五、预训练模型并行六、预训练3D并行七、预训练代码示例总结 前言 在人工智能的宏伟蓝图中&#xff0c;大语言模型&#xff08;LLM&#xff09;的预训练是构筑智慧之塔的基石。预训练过…
阅读更多...
嵌入式s5p5818核心板介绍

嵌入式s5p5818核心板介绍

底板寻址空间介绍 s5p6818 寻址空间采用统一编址方式进行管理 寻址空间映射图&#xff1a; 独立寻址&#xff1a;片内片外存储器只能选择其中一个 统一寻址&#xff1a;片内片外存储器都能使用&#xff0c;且使用的是同一片连续的寻址空间 reserved保留&#xff0c;Normaol …
阅读更多...
Ubuntu20.04安装redis5.0.7

Ubuntu20.04安装redis5.0.7

redis下载命令&#xff1a; wget https://download.redis.io/releases/redis-5.0.7.tar.gz 解压到 opt目录下 tar -zxvf redis-5.0.7.tar.gz -C /opt apt install -y gcc # 安装gccapt install make # 安装make 后面执行make一直报错 make报错后清除&#xff1a; make …
阅读更多...
【03-掌握Scikit-learn：深入机器学习的实用技术】

【03-掌握Scikit-learn：深入机器学习的实用技术】

文章目录 前言数据预处理缺失值处理数据缩放特征选择模型训练参数调整模型评估总结前言 经过了对Python和Scikit-learn的基础安装及简单应用，我们现在将更深入地探究Scikit-learn的实用技术，以进一步提升我们的数据科学技能。在本文中，我们将涵盖数据预处理、特征选择、模型…
阅读更多...
最新文章

Copyright @ 2022~2023