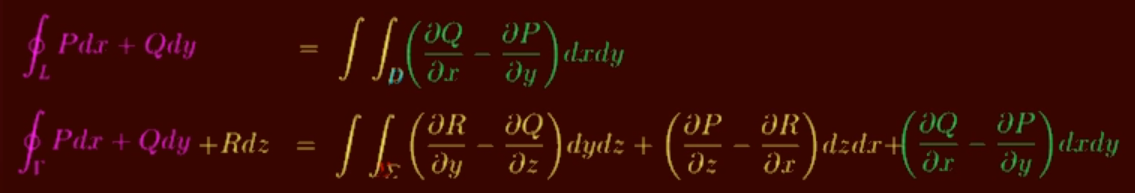文章目录
- 一、数学
- (一) 高数
- 0.初等数学补充
- 1.函数、极限、连续
- 2.导数
- 3.中值定理
- 4.积分
- 5.微分方程
- 6.空间解析几何
- 7.多元微分
- 8.重积分
- 9.曲线曲面积分
- 10.无穷级数
- 11.其他杂记
- (二) 线代
- 0.串联各章的等价条件
- 1.行列式、矩阵的秩、矩阵的初等变换
- 2.向量
- 3.方程组、矩阵方程AX=B
- 4.特征值、特征向量
- 5.二次型
- (三) 概率
- 如何刷套卷
- 二、专业课
- (一) 数据结构
- (二) 计组
- (三) 操作系统
- (四) 计网
- 咸鱼学长传记
- 三、英语
- (一) 完型
- (二) 阅读
- (三) 新题型
- (四) 翻译:划分句子成分
- (五) 作文
- 学习方法
- 1.学累了的休息方式:4s
- 2.学习感悟
- 3.对抗焦虑
一、数学
(一) 高数
0.初等数学补充
1.初等数学公式:
(1)立方和公式: a 3 + b 3 = ( a + b ) ( a 2 − a b + b 2 ) a^3+b^3=(a+b)(a^2-ab+b^2) a3+b3=(a+b)(a2−ab+b2) 【例如: 1 + x 6 = 1 + ( x 2 ) 3 = ( 1 + x 2 ) ( x 4 − x 2 + 1 ) 1+x^6=1+(x^2)^3=(1+x^2)(x^4-x^2+1) 1+x6=1+(x2)3=(1+x2)(x4−x2+1)】
(2)立方差公式: a 3 − b 3 = ( a − b ) ( a 2 + a b + b 2 ) a^3-b^3=(a-b)(a^2+ab+b^2) a3−b3=(a−b)(a2+ab+b2) 【例如: t 3 − 1 = ( t − 1 ) ( t 2 + t + 1 ) t^3-1=(t-1)(t^2+t+1) t3−1=(t−1)(t2+t+1)】
(3)球体体积: V = 4 3 π R 3 V=\dfrac{4}{3}πR^3 V=34πR3
球体的表面积: S 球表面积 = 4 π R 2 S_{球表面积}=4πR^2 S球表面积=4πR2
(4)诱导公式: ( sin θ + cos θ ) 2 2 = sin ( θ + π 4 ) (\sinθ+\cosθ)\dfrac{\sqrt{2}}{2}=\sin(θ+\dfrac{π}{4}) (sinθ+cosθ)22=sin(θ+4π)
2.高等数学拓展公式:
① x n − 1 = ( x − 1 ) ( x n − 1 + x n − 2 + . . . + x + 1 ) x^n-1=(x-1)(x^{n-1}+x^{n-2}+...+x+1) xn−1=(x−1)(xn−1+xn−2+...+x+1)
3.极坐标:
极点:原点
极轴:x轴
4.拓展
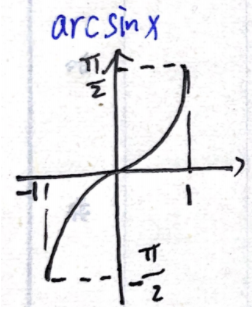
(1) arcsin x \arcsin x arcsinx
① arcsin x + arccos x = π 2 \arcsin x+\arccos x=\dfrac{π}{2} arcsinx+arccosx=2π
② arcsin 1 2 = π 6 \arcsin \dfrac{1}{2}=\dfrac{π}{6} arcsin21=6π 【 sin x = 1 2 \sin x=\dfrac{1}{2} sinx=21,则 x = π 6 x=\dfrac{π}{6} x=6π】
(2)公式: 1 2 + 2 2 + . . . + n 2 = n ( n + 1 ) ( 2 n + 1 ) 6 1²+2²+...+n^2=\dfrac{n(n+1)(2n+1)}{6} 12+22+...+n2=6n(n+1)(2n+1)
1.函数、极限、连续
1.求极限:
①非零因子可以先算出来,其他不行:
Ⅰ.同一极限号下,不能求二次极限,尤其是幂指函数。要用 x = e ln x x=e^{\ln x} x=elnx 【660 T133】 (但其他均为常数,则可直接求出来,如880 第一章综合填空4)
Ⅱ.等价无穷小只能 分子、分母 整除,内函数不可以等价代换。(如幂函数、幂指函数的指数、底数)
2.可去间断点:左右极限存在且相等
3.等价无穷小:
1 − cos α x ∼ α ( 1 − cos x ) ∼ α 2 x 2 1-\cos^αx\sim α(1-\cos x)\sim \dfrac{α}{2}x^2 1−cosαx∼α(1−cosx)∼2αx2
4.判断是夹逼原理还是定积分定义:看变化部分的最大值与主体部分相比较:
①是次量级:夹逼
②是同量级:定积分定义 【高数辅导讲义 P30】
5.幂指函数求极限:
① x = e ln x x=e^{\ln x} x=elnx
② [ 1 + α ( x ) ] β ( x ) − 1 ∼ α ( x ) ⋅ β ( x ) [1+α(x)]^{β(x)}-1\sim α(x)·β(x) [1+α(x)]β(x)−1∼α(x)⋅β(x) 【当 α ( x ) → 0 , α ( x ) ⋅ β ( x ) → 0 α(x)→0,α(x)·β(x)→0 α(x)→0,α(x)⋅β(x)→0时】
6.函数四性态:
③周期性: f ( x ) f(x) f(x)是以T为周期的可导周期函数 ⇨ f ′ ( x ) f'(x) f′(x)也是以T为周期的周期函数 【可导的周期函数的导函数,仍为周期函数 】
④有界性: f ′ ( x ) f'(x) f′(x)在有限区间I上有界 ⇒ \Rightarrow ⇒ f ( x ) f(x) f(x)在有限区间I上有界
7.开根要带绝对值: a 2 = ∣ a ∣ \sqrt{a^2}=|a| a2=∣a∣
8.求数列极限有下界:数学归纳法 【18年19.】
x 1 > 0 x_1>0 x1>0,设 x n > 0 x_n>0 xn>0,则 x n + 1 = . . . > 0 x_{n+1}=...>0 xn+1=...>0
由数学归纳法可知,对所有正整数n,有 x n > 0 x_n>0 xn>0成立
∴数列{ x n x_n xn}有下界0
2.导数
1.含绝对值的函数可以求导:分正负(x>0,x<0),分别求导,导函数是分段函数 【660 T152】
结论: ∣ x ∣ x n |x|x^n ∣x∣xn 在x=0处n阶可导
2.增减区间的书写规范:
①多个增(减)区间 用 , 或 和 连接
②同一用开区间 (),避免端点没有定义或者端点不单调
3.导数公式:
① ( tan x ) ′ = sec x 2 (\tan x)'=\sec x^2 (tanx)′=secx2
② ( sec x ) ′ = sec x tan x (\sec x)'=\sec x\tan x (secx)′=secxtanx
4.导数定义:
(1)导函数的定义
① y ′ = lim Δ x → 0 f ( x + Δ x ) − f ( x ) Δ x y'=\lim\limits_{Δx→0}\dfrac{f(x+Δx)-f(x)}{Δx} y′=Δx→0limΔxf(x+Δx)−f(x)
② f ′ ( x ) = lim h → 0 f ( x + h ) − f ( x ) h f'(x)=\lim\limits_{h→0}\dfrac{f(x+h)-f(x)}{h} f′(x)=h→0limhf(x+h)−f(x) 【15年18.】
3.中值定理
1.微分中值定理证明题:
(1)第一问的结论,往往作为求证第二问的条件
中值定理:【13年18、16年19】
(2)方程的根、证明不等式、微分中值定理:
基本思想:①移到一边 ②设辅助函数,看奇偶性 ③求导
2.证明拉格朗日中值定理:【09年18.】
构造辅助函数F(x)=f(x)-g(x),用罗尔定理F(a)=F(b)=0
3.方程的根的存在性及个数:【11年17、17年18】
4.介值定理:
f(x)在[a,b]上连续,C介于f(a)和f(b)之间。则 ∃ ξ ∈ ( a , b ) \exist ξ∈(a,b) ∃ξ∈(a,b)使得 f ( ξ ) = C f(ξ)=C f(ξ)=C。
5.放缩:
①绝对值: ∣ a ± b ∣ ≤ ∣ a ∣ + ∣ b ∣ |a±b|≤|a|+|b| ∣a±b∣≤∣a∣+∣b∣
②最大值函数max: a + b ≤ 2 max { a , b } a+b≤2\max\{a,b\} a+b≤2max{a,b}
6.泰勒公式
(1)泰勒公式:
f ( x ) = f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) + f ′ ′ ( x 0 ) 2 ! ( x − x 0 ) 2 + f ′ ′ ′ ( x 0 ) 3 ! ( x − x 0 ) 3 + . . . + f ( n ) ( x 0 ) n ! ( x − x 0 ) n + R n ( x ) f(x)=f(x_0)+f'(x_0)(x-x_0)+\dfrac{f''(x_0)}{2!}(x-x_0)^2+\dfrac{f'''(x_0)}{3!}(x-x_0)^3+...+\dfrac{f^{(n)}(x_0)}{n!}(x-x_0)^n+\rm R_n(x) f(x)=f(x0)+f′(x0)(x−x0)+2!f′′(x0)(x−x0)2+3!f′′′(x0)(x−x0)3+...+n!f(n)(x0)(x−x0)n+Rn(x)
(2)麦克劳林公式:令 x 0 = 0 x_0=0 x0=0
f ( x ) = f ( 0 ) + f ′ ( 0 ) x + f ′ ′ ( 0 ) 2 ! x 2 + f ′ ′ ′ ( 0 ) 3 ! x 3 + . . . + f ( n ) ( 0 ) n ! x n + o ( x n ) f(x)=f(0)+f'(0)x+\dfrac{f''(0)}{2!}x^2+\dfrac{f'''(0)}{3!}x^3+...+\dfrac{f^{(n)}(0)}{n!}x^n+o(x^n) f(x)=f(0)+f′(0)x+2!f′′(0)x2+3!f′′′(0)x3+...+n!f(n)(0)xn+o(xn)
(3)泰勒公式展开
展开到几次:
Ⅰ.加减关系:同次幂系数相加减不为0
Ⅱ.乘除关系:上下同此幂
Ⅲ.泰勒展开,展少了,会导致系数不对。尤其是展开项要乘多项式的时候,容易漏。
展多了,计算了一些没用的数值,浪费考试时间。
例如:16年12. 求 f ′ ′ ′ ( 0 ) f'''(0) f′′′(0),就展开到3阶, f ′ ′ ′ ( 0 ) 3 ! = a 3 \dfrac{f'''(0)}{3!}=a_3 3!f′′′(0)=a3
7.极值点与拐点:
①可导函数,某点若是极值点则一定不是拐点,若为拐点则一定不为极值点。
② f ( x ) f(x) f(x)在某点不可导 (如分段函数的分界点),则可能同时为极值点和拐点。
变上限积分的链式求导错误,导致f’(x)求错,无法消去多余项,导致驻点求不出。【10年16】
8.渐近线:
偶函数的渐近线:偶函数关于x=0对称,只求x→+∞方向,然后左右对称。
①水平渐近线:右边有,左边就是共享同一条 【0或1条】
②垂直渐近线:若有,1条x=0 或 偶数条垂直渐近线(左右对称) 【0,1,2,4,…】
③斜渐近线:
Ⅰ.若偶函数有水平渐近线,则两方向均无斜渐近线【0条)】
Ⅱ.若偶函数无水平渐近线,则有 0或2条 斜渐近线。若偶函数在x→+∞时有斜渐近线 y = a x + b y=ax+b y=ax+b,则x→-∞有斜渐近线 y = − a x + b y=-ax+b y=−ax+b
9.不等式问题:
(1)函数不等式:
①先看奇偶性,用f(-x)去试。若为偶函数,则只需要证明右半边。尤其是x属于对称区间。【12年15.】
②移到一边构造辅助函数,求导看单调性。
③若f’(x)不好看出正负:Ⅰ.放缩:根据x的取值范围,进行适当的放缩,使得导数>0或<0 。Ⅱ.求二阶导
10.证明常用:
(1) cos x \cos x cosx 在 ( 0 , π 2 ) (0,\dfrac{π}{2}) (0,2π)上单调减少
【2014年19:当 0 < a n < π 2 , 0 < b n < π 2 0<a_n<\dfrac{π}{2},0<b_n<\dfrac{π}{2} 0<an<2π,0<bn<2π时,若有 cos b n < cos a n \cos b_n<\cos a_n cosbn<cosan,∵ cos x \cos x cosx 在 ( 0 , π 2 ) (0,\dfrac{π}{2}) (0,2π)上单调减少 ∴ 0 < a n < b n < π 2 0<a_n<b_n<\dfrac{π}{2} 0<an<bn<2π】
(2)基本不等式
① sin x < x < tan x , x ∈ ( 0 , π 2 ) \sin x<x<\tan x,x∈(0,\dfrac{π}{2}) sinx<x<tanx,x∈(0,2π)
② x 1 + x < ln ( 1 + x ) < x , x ∈ ( 0 , + ∞ ) \dfrac{x}{1+x}<\ln(1+x)<x,x∈(0,+∞) 1+xx<ln(1+x)<x,x∈(0,+∞) ⇨ 1 n + 1 < ln ( 1 + 1 n ) < 1 n \dfrac{1}{n+1}<\ln(1+\dfrac{1}{n})<\dfrac{1}{n} n+11<ln(1+n1)<n1
③ a 2 + b 2 ≥ 2 a b a^2+b^2≥2ab a2+b2≥2ab
④ ∣ x ± y ∣ ≤ ∣ x ∣ + ∣ y ∣ |x±y|≤|x|+|y| ∣x±y∣≤∣x∣+∣y∣ (和差的绝对值 不超过 绝对值的和)
4.积分
1.不定积分公式: ∫ 1 a 2 + x 2 d x = 1 a arctan x a + C \int\dfrac{1}{a^2+x^2}dx=\dfrac{1}{a}\arctan\dfrac{x}{a}+C ∫a2+x21dx=a1arctanax+C
∫ sec 2 x d x = tan x + C \int\sec^2xdx=\tan x+C ∫sec2xdx=tanx+C
∫ sec x tan x d x = sec x + C \int\sec x\tan xdx=\sec x+C ∫secxtanxdx=secx+C
∫ sec x d x = ln ∣ sec x + tan x ∣ + C \int\sec xdx=\ln|\sec x+\tan x|+C ∫secxdx=ln∣secx+tanx∣+C
2.变上限积分的可导性:
f ( x ) f(x) f(x)在 [ a , b ] [a,b] [a,b]上除 x = x 0 ∈ ( a , b ) x=x_0∈(a,b) x=x0∈(a,b)外均连续,则在点 x = x 0 x=x_0 x=x0处,则
| f(x)在 x = x 0 x=x_0 x=x0处 | ∫ a x f ( t ) d t \int_a^xf(t)dt ∫axf(t)dt |
|---|---|
| ①连续 | 可导 |
| ②可去间断点 | 可导 |
| ③跳跃间断点 | 连续但不可导 |
3.反常积分判敛散性:
先看是两种反常积分的哪一种,若两种都包含,则拆分区间拆成两种 【16年1.】
(1)定义:凑微分求出原函数,代入端点值看是否收敛
(2)比较判别法:
(3)P积分:
4.三角代换
a 2 + x 2 \sqrt{a^2+x^2} a2+x2 令 x = a tan t x=a\tan t x=atant
5.微分方程
6.空间解析几何
1.两面垂直 ⇔ \Leftrightarrow ⇔ n 1 ⃗ ⊥ n 2 ⃗ \vec{n_1}⊥\vec{n_2} n1⊥n2 ⇔ \Leftrightarrow ⇔ n 1 ⃗ ⋅ n 2 ⃗ = 0 \vec{n_1}·\vec{n_2}=0 n1⋅n2=0
xOy面:即z=0。法向量为 (0,0,1)
2.曲面与空间曲线:
(1)旋转曲面 【13年19.】
(2)投影曲线 【17年19.(1)】
7.多元微分
1.多元函数
z = f ( u ) = f ( e x cos y ) z=f(u)=f(e^x\cos y) z=f(u)=f(excosy)是一元函数, f ′ = f ′ , f ′ ′ = f ′ ′ f'=f',f''=f'' f′=f′,f′′=f′′
2.梯度:
梯度的模: ∣ g r a d f ∣ ⃗ = ( ∂ f ∂ x ) 2 + ( ∂ f ∂ y ) 2 = f x ′ 2 + f y ′ 2 |\vec{\rm gradf|}=\sqrt{(\dfrac{∂f}{∂x})^2+(\dfrac{∂f}{∂y})^2}=\sqrt{f'^2_x+f'^2_y} ∣gradf∣=(∂x∂f)2+(∂y∂f)2=fx′2+fy′2 【15年17.】
8.重积分
1.求质心、形心,注意对称性:关于x轴对称则 y ˉ = 0 \bar{y}=0 yˉ=0;关于y轴对称则 x ˉ = 0 \bar{x}=0 xˉ=0 【13年19.】
9.曲线曲面积分
1.曲面的侧判断曲面是否封闭:
(1)内侧、外侧:已封闭,直接用高斯公式 【21年14.】
(2)上侧、下侧、左侧、右侧、前侧、后侧:未封闭,补面用高斯公式
10.无穷级数
1.泰勒级数
arctan x = ∑ n = 0 ∞ ( − 1 ) n x 2 n + 1 2 n + 1 = ∑ n = 1 ∞ ( − 1 ) n − 1 x 2 n − 1 2 n − 1 ( − 1 ≤ x ≤ 1 ) = x − x 3 3 + x 5 5 + . . . \arctan x=\sum\limits_{n=0}^∞(-1)^n\dfrac{x^{2n+1}}{2n+1}=\sum\limits_{n=1}^∞(-1)^{n-1}\dfrac{x^{2n-1}}{2n-1} \quad (-1≤x≤1)=x-\dfrac{x^3}{3}+\dfrac{x^5}{5}+... arctanx=n=0∑∞(−1)n2n+1x2n+1=n=1∑∞(−1)n−12n−1x2n−1(−1≤x≤1)=x−3x3+5x5+...
2.求幂级数的和函数:
(1)提出x作分母:对x≠0,x=0分类讨论。 【2012年17】
(2)要用逐项求导,先求收敛区间。 【2013年16(1)】
3.逐项求导,只在开区间(-R,R)上成立。端点值要单独讨论。 【2021年18(2)】
11.其他杂记
1.高数常用技巧:减项、加项
2.简化计算:
(1)等价变形:
① ln 1 + x 1 − x = ln ( 1 + x ) − ln ( 1 − x ) \ln\dfrac{1+x}{1-x}=\ln(1+x)-\ln(1-x) ln1−x1+x=ln(1+x)−ln(1−x)
② ln ( 1 + e x ) = x + ln ( 1 + e − x ) \ln(1+e^x)=x+\ln(1+e^{-x}) ln(1+ex)=x+ln(1+e−x) 【提出ex】
(2)图形面积
① ∫ 0 π sin x = 2 \int_0^{π}\sin x=2 ∫0πsinx=2, ∫ 0 π sin 2 x = π 2 \int_0^{π}\sin^2 x=\dfrac{π}{2} ∫0πsin2x=2π
② ∫ 0 + ∞ e − x = 1 \int_0^{+∞}e^{-x}=1 ∫0+∞e−x=1
3.多元积分:【第二类线面是重点】
(1)三大公式【均是求二类】
格林公式:封闭的二维二类线积分→二重积分
斯托克斯公式:封闭的三维二类线积分→曲面积分 (平面则用一类面,曲面用二类面)
高斯公式:二类面积分→三重积分
(2)奇偶性:
圆(球)、椭圆(椭球),关于x轴、y轴 (xoy、yoz、zox面)均对称,遇到x、y、z的奇函数,其二重积分、三重积分、一类线、一类面积分为0
(3)形心公式
求二重积分、三重积分、一类线ds、一类面dS对x,y,z的积分时,可以考虑形心公式。
如: ∮ x d s = x ˉ ⋅ l \oint xds=\bar{x}·l ∮xds=xˉ⋅l
4.①牛顿-莱布尼茨公式: f ( x 2 ) − f ( x 1 ) = ∫ L d f = ∫ x 1 x 2 d f d t d t f(x_2)-f(x_1)=\int_Ldf=\int_{x_1}^{x_2}\dfrac{df}{dt}dt f(x2)−f(x1)=∫Ldf=∫x1x2dtdfdt 【联系了积分和微分】
②Green公式: ∮ L P d x + Q d y = ∬ D ( ∂ Q ∂ x − ∂ P ∂ y ) d x d y \oint_LPdx+Qdy=\iint_D(\dfrac{∂Q}{∂x}-\dfrac{∂P}{∂y})dxdy ∮LPdx+Qdy=∬D(∂x∂Q−∂y∂P)dxdy 【联系了封闭的第二类曲线积分和二重积分】
③斯托克斯公式是格林公式的推广:若把斯托克斯公式的第三列的第二行、第三行都取0,然后按第三列展开,发现就是格林公式。
④Gauss公式: ∯ Σ P d y d z + Q d z d x + R d x d y = ∭ Ω ( ∂ P ∂ x + ∂ Q ∂ y + ∂ R ∂ z ) d v \oiint_Σ Pdydz+Qdzdx+Rdxdy=\iiint\limits_Ω(\dfrac{∂P}{∂x}+\dfrac{∂Q}{∂y}+\dfrac{∂R}{∂z})dv ∬ΣPdydz+Qdzdx+Rdxdy=Ω∭(∂x∂P+∂y∂Q+∂z∂R)dv 【联系了封闭的第二类曲面积分和三重积分】
5.高斯公式 + 有奇点,要挖洞:
I = ∯ Σ = ∯ Σ + Σ 1 − ∯ Σ 1 I=\oiint\limits_Σ=\oiint\limits_{Σ+Σ_1}-\oiint\limits_{Σ_1} I=Σ∬=Σ+Σ1∬−Σ1∬
6.武老师押题:
①数列极限,22 23考的泰勒
②不考傅里叶级数,23考过。傅里叶级数只会出选填。
③二类线积分 (我猜大概率是格林 + 挖洞 ),22考的二型线 斯托克斯,23考的二类面 高斯
7.第二型曲面积分的含义是:对三维空间中的曲面,在二维平面上的投影做二重积分

8.空间曲面的面积× cos γ \cosγ cosγ=投影到xoy平面的面积
空间曲面的面积 = ∬ Σ 1 d S =\iint\limits_Σ1dS =Σ∬1dS
投影到xoy平面的面积 = ∬ D 1 d σ =\iint\limits_D1dσ =D∬1dσ
cos γ = 1 1 + z x 2 + z y 2 \cosγ=\dfrac{1}{\sqrt{1+z^2_x+z^2_y}} cosγ=1+zx2+zy21
9.第二类曲面积分,对dxdy就是投影到xoy面。若f(x)投影到xoy面是一条直线或曲线,不是投影成带阴影的面积,则积分为0。【二类面,直接法,投影成线,积分为0】
10.画空间平面的方法(求曲线曲面积分时):如x+y+z=0、x+y+z=1、z=x+y (x+y-z=0)
①令z=0,得xoy面上的直线
②根据平面方程易得平面法向量。根据法向量的方向将平面直线延伸为空间平面。
11.选择题:
①直接法
②排除法:具体函数法、特殊值法
排除法尽量用在:①直接法不方便求解、计算繁琐 ②验证答案 时使用
举例:讲义P156例2
12.高数真题:
(1)多元微分怎么考?
选择考概念,大题考多元极值、最值
(2)无穷级数怎么考?
选择考常数项级数的敛散性判断,大题考求和函数
(3)数一的高数4道大题都考哪些考点?
①求函数极限、导数和微分方程的几何应用:求单调区间和极值、多元微分求极值
②无穷级数:求和函数
③数列极限:递推、夹逼/单调有界求极限
④曲线曲面积分、旋转曲面、多元微分集合应用
⑤微分中值定理
(二) 线代
0.串联各章的等价条件
1. ①A可逆
⇦⇨②|A|≠0
⇦⇨③r(A)=n,A满秩
⇦⇨④Ax=0仅有零解
⇦⇨⑤A的列向量 α₁,α₂,…αn线性无关
⇦⇨⑥A的特征值均不为0 【17年5.】
2. ①A不可逆
⇦⇨②|A|=0
⇦⇨③r(A)<n,A不满秩
⇦⇨④Ax=0有非零解
⇦⇨⑤A的列向量 α₁,α₂,…αn线性相关
⇦⇨⑥A有零特征值
1.行列式、矩阵的秩、矩阵的初等变换
1. r ( A ) = k r(A)=k r(A)=k:
最高阶非零子式的阶数为k;至少存在一个k阶子式不为0,所有高于k阶的子式全为0
2. r ( A ) = 1 r(A)=1 r(A)=1,则:
①特征值为 tr(A) 及 n-1个0
②tr(A)≠0,则A可相似对角化;tr(A)=0,则A不可相似对角化。
3.秩的性质:
(1) r ( A ) \rm r(A) r(A) = r ( A T ) = r ( A A T ) = \rm =r(A^T)=r(AA^T)= =r(AT)=r(AAT)= r ( A T A ) \rm r(A^TA) r(ATA) 【2012年21(1)】
(2) r ( A + B ) ≤ r ( A ) + r ( B ) \rm r(A+B)≤r(A)+r(B) r(A+B)≤r(A)+r(B) 【2013年21(2)】
4.初等矩阵:
①互换初等矩阵 E i j E_{ij} Eij的逆和转置为本身: E i j − 1 = E i j = E i j T {E_{ij}}^{-1}=E_{ij}={E_{ij}}^T Eij−1=Eij=EijT
②倍加初等矩阵 E i j ( k ) E_{ij}(k) Eij(k): [ E i j ( k ) ] − 1 = E i j ( − k ) [E_{ij}(k)]^{-1}=E_{ij}(-k) [Eij(k)]−1=Eij(−k)
【 E i j ( k ) E_{ij}(k) Eij(k):第i列的k倍加到第j列,或 第j行的k倍加到第i行】
5.矩阵的初等变换:
(1)左乘行变换,右乘列变换
(2)矩阵A可经初等列变换化为矩阵B ⇦⇨ 矩阵方程AX=B有解 ⇦⇨ r(A)=r(A,B) 【18年21.】
2.向量
1.向量个数与维数的关系:
①方程个数<未知数个数,即个数>维数,则线性相关。
②n维向量空间,若要向量组线性无关,最多只能有n个向量。即:若线性无关,则个数≤维数 (逆否命题)
2.向量空间:向量 = 基 ·坐标
β = ( α 1 , α 2 , α 3 ) ⋅ ( x 1 x 2 x 3 ) = x 1 α 1 + x 2 α 2 + x 3 α 3 β =(α_1,α_2,α_3)·\left(\begin{array}{c} x_1 \\ x_2 \\ x_3 \end{array}\right)=x_1α_1+x_2α_2+x_3α_3 β=(α1,α2,α3)⋅ x1x2x3 =x1α1+x2α2+x3α3
3.向量空间:过渡矩阵:原基 右乘过渡矩阵,到新基
A P = B AP = B AP=B,则 P = A − 1 B P=A^{-1}B P=A−1B
小技巧: ( A ∣ B ) → ( E ∣ A − 1 B ) (A|B)→(E|A^{-1}B) (A∣B)→(E∣A−1B)
4.n维非零列向量的性质:
对任意非零列向量 α,β,有以下性质:
① r ( β α T ) = r ( α α T ) = r ( β β T ) = 1 \rm r(βα^T)=r(αα^T)=r(ββ^T)=1 r(βαT)=r(ααT)=r(ββT)=1 【2013年21(2)】
② t r ( β α T ) = α T β \rm tr(βα^T)=α^Tβ tr(βαT)=αTβ, t r ( α α T ) = α T α , t r ( β β T ) = β T β \rm tr(αα^T)=α^Tα,tr(ββ^T)=β^Tβ tr(ααT)=αTα,tr(ββT)=βTβ
3.方程组、矩阵方程AX=B
1.Ax=0有非零解:
⇦⇨ |A|=0 【15年20.(2)】
⇦⇨ A的列向量 α1,α2,…,αn 线性相关
⇦⇨ r(A)<n
⇦⇨ A不可逆
(1)证明 α 1 , α 2 , … α n α₁,α₂,…α_n α1,α2,…αn线性无关:【09年20.(Ⅱ)】
①定义法
②|A|≠0
(2) A 11 ≠ 0 A_{11}≠0 A11=0 (除去第一行第一列的剩下n-1阶矩阵不全为0),则:
① r ( A ) ≥ n − 1 r(A)≥n-1 r(A)≥n−1
② α 2 , α 3 , . . . , α n α_2,α_3,...,α_n α2,α3,...,αn线性无关
2.非齐次线性方程组的几何意义
3.同解方程组的充要条件:行向量组等价
4.方程组Ax=0与Bx=0的公共解:
①A、B都为具体的方程组: 公共解为 联立方程组 ( A B ) x = 0 \dbinom{A}{B}x=0 (BA)x=0的解
②A为具体方程组,B为基础解系:将B的通解代入A
③A、B均为基础解系:r=通解1=通解2=通解1-通解2
5.Ax=0:相关性
Ax=β:表示性
6.非齐次Am×nx=β有两个不同的解 : 【880 方程组综合选择3、数一2010年20.】
⇨ 齐次Ax=0有非零解 ⇦⇨ r(A)<n,A的列向量组线性相关
⇦⇨r(A)=r(A|b)<n,Am×nx=β有无穷多解
7.与Ax=0的基础解系等价的线性无关的向量组,也是Ax=0的基础解系 [880 方程组 综合解答3]
8.写行列式、矩阵,注意不要漏抄负号、平方号!
9.求非齐次特解:令自由变量均为0
求齐次通解:令自由变量为 (1,0) (0,1)
4.特征值、特征向量
1.相似: P − 1 A P = B P^{-1}AP=B P−1AP=B,则 A ∼ B A\sim B A∼B
相似对角化: P − 1 A P = Λ P^{-1}AP=Λ P−1AP=Λ,则 A ∼ Λ A\sim Λ A∼Λ
2.相似与合同
相似⇨特征值相同、秩相同:r(A)=r(B)、r(λE-A)=r(λE-B)
合同⇨正负惯性指数相同
3.求特征值λ对应的特征向量:
①求出 ( λ E − A ) x = 0 (λE-A)x=0 (λE−A)x=0的基础解系 ξ 1 , ξ 2 , . . . , ξ n ξ_1,ξ_2,...,ξ_n ξ1,ξ2,...,ξn
②矩阵A的属于特征值λ的全部特征向量为:齐次方程组 ( λ E − A ) x = 0 (λE-A)x=0 (λE−A)x=0的通解去掉零解,即 k 1 ξ 1 + k 2 ξ 2 + . . . + k n ξ n k_1ξ_1+k_2ξ_2+...+k_nξ_n k1ξ1+k2ξ2+...+knξn (k1,k2,…,kn不全为0)
即 全部特征向量,是方程组 ( λ E − A ) x = 0 (λE-A)x=0 (λE−A)x=0的非零通解
4.求可逆矩阵P,使得 P − 1 A P = Λ P^{-1}AP=Λ P−1AP=Λ:
①求全部特征值 λ₁ λ₂ λ₃和对应的特征向量 α₁ α₂ α₃
②令 P = ( α 1 , α 2 , α 3 ) P=(α₁,α₂,α₃) P=(α1,α2,α3),则 P − 1 A P = Λ = ( λ 1 λ 2 λ 3 ) P^{-1}AP=Λ=\left(\begin{array}{cc} λ₁ & & \\ & λ₂ & \\ & & λ₃\\ \end{array}\right) P−1AP=Λ= λ1λ2λ3
5.已知矩阵A、B。要求可逆矩阵P,使得 P − 1 A P = B P^{-1}AP=B P−1AP=B。
我们没有学过直接相似的定理。都需要经过对角矩阵来实现传递性,即 A ∼ Λ , B ∼ Λ A\sim Λ,B\sim Λ A∼Λ,B∼Λ ⇨ A ∼ B A\sim B A∼B。即有 P 1 − 1 A P 1 = Λ , P 2 − 1 B P 2 = Λ P_1^{-1}AP_1=Λ,P_2^{-1}BP_2=Λ P1−1AP1=Λ,P2−1BP2=Λ, ∴ P 1 − 1 A P 1 = P 2 − 1 B P 2 ∴P_1^{-1}AP_1=P_2^{-1}BP_2 ∴P1−1AP1=P2−1BP2, ∴ P 2 P 1 − 1 A P 1 P 2 − 1 = B ∴P_2P_1^{-1}AP_1P_2^{-1}=B ∴P2P1−1AP1P2−1=B。即 存在 P = P 1 P 2 − 1 P=P_1P_2^{-1} P=P1P2−1,使得 P − 1 A P = B P^{-1}AP=B P−1AP=B 【14年21.】
6.施密特正交化:
β 1 = α 1 β₁=α₁ β1=α1
β 2 = α 2 − ( α 2 , β 1 ) ( β 1 , β 1 ) β 1 β₂=α₂-\dfrac{(α₂,β₁)}{(β₁,β₁)}β₁ β2=α2−(β1,β1)(α2,β1)β1
β 3 = α 3 − ( α 3 , β 1 ) ( β 1 , β 1 ) β 1 − ( α 3 , β 2 ) ( β 2 , β 2 ) β 2 β₃=α₃-\dfrac{(α₃,β₁)}{(β₁,β₁)}β₁-\dfrac{(α₃,β₂)}{(β₂,β₂)}β₂ β3=α3−(β1,β1)(α3,β1)β1−(β2,β2)(α3,β2)β2
7.定理:
设A是m×n矩阵,若 r ( A ) = r < n r(A)=r<n r(A)=r<n,则齐次线性方程组 A x = 0 Ax=0 Ax=0 存在基础解系,并且基础解系由 n − r n-r n−r 个线性无关的解向量构成
s=n-r:齐次线性方程组Ax=0的基础解系中线性无关的解向量的个数 = 自由变量的个数
8.若λ=a是A的二重特征值:
则λ=a对应2个线性无关的特征向量,s=n-r(aE-A)=2
∴r(aE-A)=n-s=3-2=1
9. s = n − r ( λ E − A ) \rm s=n-r(λE-A) s=n−r(λE−A)的含义:【14年21.】
方程组 ( λ E − A ) x = 0 (λE-A)x=0 (λE−A)x=0有s个线性无关的解
齐次线性方程组 ( λ E − A ) x = 0 (λE-A)x=0 (λE−A)x=0的基础解系有 s=n-r(λE-A)个解向量
∵基础解系的解向量线性无关
∴ ( λ E − A ) x = 0 (λE-A)x=0 (λE−A)x=0有 s=n-r(λE-A )个线性无关的特征向量
【n为矩阵的列数,即未知数的个数。 [若A的n×m矩阵,则s=m-r]】
9. A 2 = A A^2=A A2=A ⇨ λ 2 = λ λ^2=λ λ2=λ
10.完全立方公式:
( a + b ) 3 = a 3 + 3 a 2 b + 3 a b 2 + b 3 (a+b)^3=a^3+3a^2b+3ab^2+b^3 (a+b)3=a3+3a2b+3ab2+b3
( a − b ) 3 = a 3 − 3 a 2 b + 3 a b 2 − b 3 (a-b)^3=a^3-3a^2b+3ab^2-b^3 (a−b)3=a3−3a2b+3ab2−b3
例: λ 3 + 3 λ 2 + 3 λ + 1 = ( λ + 1 ) 3 λ^3+3λ^2+3λ+1=(λ+1)^3 λ3+3λ2+3λ+1=(λ+1)3
11.特征值的性质:
(4)设 f ( x ) f(x) f(x)为多项式,若 λ 1 , λ 2 , . . . , λ n λ_1,λ_2,...,λ_n λ1,λ2,...,λn为A的特征值,则 f ( λ 1 ) , f ( λ 2 ) , . . . , f ( λ n ) f(λ_1),f(λ_2),...,f(λ_n) f(λ1),f(λ2),...,f(λn)为 f ( A ) f(A) f(A)的特征值 【17年5.】

12.行和相等的矩阵的性质:(以三阶矩阵A为例,每行元素之和均为k)
行和k 是A的一个特征值, ( 1 1 1 ) \left(\begin{array}{c} 1 \\ 1 \\ 1 \end{array}\right) 111 是对应 行和k 的一个特征向量
5.二次型
1.二次型与二次曲面:
解|λE-A|=0,求A的特征值,判断曲面类型
3.三种变换:
①线性变换:旋转、拉伸
②正交变换:仅旋转,不做拉伸。正交变换不改变向量的长度,||x||=||y||,是一种等距变换。(P为正交矩阵,则 P T = P − 1 P^T=P^{-1} PT=P−1)
③配方法:旋转、拉伸,研究正负惯性指数
4.①初等变换不改变矩阵的秩,可能改变特征值、迹、行列式的值。
②相似变换和正交变换,不改变矩阵的特征值。
5.正交变换:
(1)求正交变换 X=QY,或 求正交矩阵Q:
①|λE-A|=0,求所有特征值 λ₁ λ₂ λ₃
②求每个特征值对应的特征向量 是ξ₁ ξ₂ ξ₃
③将特征向量正交化、单位化,得 α₁ α₂ α₃。拼起来得正交矩阵Q=(α₁,α₂,α₃)
(2) Q − 1 A Q = Q T A Q = ( λ 1 λ 2 λ 3 ) Q^{-1}AQ=Q^TAQ=\left(\begin{array}{cc} λ₁ & & \\ & λ₂ & \\ & & λ₃\\ \end{array}\right) Q−1AQ=QTAQ= λ1λ2λ3 ,Q的列向量 α 1 , α 2 , α 3 α_1,α_2,α_3 α1,α2,α3就是矩阵A的对应于特征值 λ 1 , λ 2 , λ 3 λ_1,λ_2,λ_3 λ1,λ2,λ3的特征向量
正交变换不改变原图形的面积
6.配方法
(1)先凑所有含 x 1 x_1 x1的,再凑所有含 x 2 x_2 x2的,最后剩下 x 3 x_3 x3。令 y 1 , y 2 , y 3 y_1,y_2,y_3 y1,y2,y3分别等于这些平方项目
(2)若没有平方项,则创造平方项:令 { x 1 = y 1 + y 2 x 2 = y 1 − y 2 x 3 = y 3 \left\{\begin{aligned} x_1&=y_1+y_2\\ x_2&=y_1-y_2\\ x_3&=y_3 \end{aligned}\right. ⎩ ⎨ ⎧x1x2x3=y1+y2=y1−y2=y3
7.若二次型 f ( x 1 , x 2 , x 3 ) f(x_1,x_2,x_3) f(x1,x2,x3)在正交变换X=PY下的标准型为 2 y 1 2 + y 2 2 − y 3 2 2y_1^2+y_2^2-y_3^2 2y12+y22−y32 ,即 P T A P = ( 2 1 − 1 ) P^TAP=\left(\begin{array}{cc} 2 & & \\ & 1 & \\ && -1 \end{array}\right) PTAP= 21−1
8.正定二次型:
(1)定义:
当且仅当 x = 0 x=0 x=0 时,才有 f = x T A x = 0 f=x^TAx=0 f=xTAx=0。当 x ≠ 0 x≠0 x=0 时都有 f = x T A x > 0 f=x^TAx>0 f=xTAx>0,则 f f f为正定二次型
(2)性质:
①各阶顺序主子式 Δ i > 0 Δ_i>0 Δi>0
②特征值均为正 λ i > 0 λ_i>0 λi>0
9.二次型
f ≥ 0 f≥0 f≥0,则 f f f的负惯性指数为0
反证法:若f负惯性指数不为0,不妨设f=y₁²+y₂²-y₃²,取y₁=0,y₂=0,y₃=1,得f=-1<0。与f>=0矛盾.故f≥0时,f的负惯性指数为0
李烈老师线代押题:
①化二次型为二次型:正交变换法、配方法
②化二次型为标准型的应用:解方程组、证明瑞丽商、矩阵开方
③数二数三:相似对角化
(三) 概率
概率大题:①求概率密度 ②求数字特征 ③求矩估计、最大似然估计
1.一维连续型随机变量X的分布函数:
F ( x ) = P { X ≤ x } = ∫ − ∞ x f ( t ) d t F(x)=P\{X≤x\}=\int_{-∞}^xf(t)dt F(x)=P{X≤x}=∫−∞xf(t)dt
P { X > a } = 1 − P { X ≤ a } = 1 − F ( a ) = ∫ a + ∞ f ( x ) d x P\{X>a\}=1-P\{X≤a\}=1-F(a)=\int_a^{+∞}f(x)dx P{X>a}=1−P{X≤a}=1−F(a)=∫a+∞f(x)dx
2.二维连续型随机变量的概率密度: P { ( X , Y ) ∈ D } = ∬ D f ( x , y ) d x d y P\{(X,Y)∈D\}=\iint\limits_Df(x,y){\rm d}x{\rm d}y P{(X,Y)∈D}=D∬f(x,y)dxdy
例如: F Z ( z ) = P { Z ≤ z } = P { X + Y ≤ z } = ∬ x + y ≤ z f ( x , y ) d x d y F_Z(z)=P\{Z≤z\}=P\{X+Y≤z\}=\iint\limits_{x+y≤z}f(x,y)dxdy FZ(z)=P{Z≤z}=P{X+Y≤z}=x+y≤z∬f(x,y)dxdy
3.二维连续型随机变量的联合分布律、联合概率密度
①由f(x,y)求F(x,y): F ( x , y ) = ∫ − ∞ y ∫ − ∞ x f ( x , y ) d x d y F(x,y)=\int_{-∞}^y\int_{-∞}^xf(x,y)dxdy F(x,y)=∫−∞y∫−∞xf(x,y)dxdy
②由F(x,y)求f(x,y): f ( x , y ) = ∂ 2 F ( x , y ) ∂ x ∂ y f(x,y)=\dfrac{∂^2F(x,y)}{∂x∂y} f(x,y)=∂x∂y∂2F(x,y) [F(x,y)可导或f(x,y)在(x,y)连续]
4.求Z的概率密度:【17年23.(1)】
步骤:
①先求分布函数: F Z ( z ) = P { Z ≤ z } = . . . F_Z(z)=P\{Z≤z\}=... FZ(z)=P{Z≤z}=...,代入Z的表达式,对自变量的取值范围进行分类讨论
②再求导: f Z ( z ) = F Z ′ ( z ) f_Z(z)=F_Z'(z) fZ(z)=FZ′(z)
5.正态分布的独立可加性 【12年23(1)】
若X与Y分别服从正态分布 N ( μ 1 , σ 1 2 ) N(μ_1,σ_1^2) N(μ1,σ12)与 N ( μ 2 , σ 2 2 ) N(μ_2,σ_2^2) N(μ2,σ22),且X与Y相互独立。
则 Z = X − Y Z=X-Y Z=X−Y也服从正态分布, Z ∼ N ( μ 1 − μ 2 , σ 1 2 + σ 2 2 ) Z\sim N( μ_1-μ_2, σ_1^2+σ_2^2) Z∼N(μ1−μ2,σ12+σ22)
6.边缘概率密度:
f X ( x ) = ∫ − ∞ + ∞ f ( x , y ) d y f_X(x) = \int_{-∞}^{+∞}f(x,y){\rm d}y fX(x)=∫−∞+∞f(x,y)dy 【注意上下限是代y的取值,x是常数,所以最后得到的是关于x的函数】
f Y ( y ) = ∫ − ∞ + ∞ f ( x , y ) d x f_Y(y) = \int_{-∞}^{+∞}f(x,y){\rm d}x fY(y)=∫−∞+∞f(x,y)dx 【例题:880多维随机变量 基础解答(5)Ⅰ】
7.条件概率密度
f Y ∣ X ( y ∣ x ) = f ( x , y ) f X ( x ) f_{Y|X}(y|x)=\dfrac{f(x,y)}{f_X(x)} fY∣X(y∣x)=fX(x)f(x,y)
8.判断两变量是否相互独立:积事件的概率 是否等于 事件概率的乘积
P { U ≤ a , X ≤ b } = P { U ≤ a } ⋅ P { X ≤ b } P\{U≤a,X≤b\}=P\{U≤a\}·P\{X≤b\} P{U≤a,X≤b}=P{U≤a}⋅P{X≤b} 【16年22(2)、880数字特征 基础解答(4)Ⅲ】
9.数字特征
(1)期望E(X):
①离散型: E ( X ) = ∑ k = 1 ∞ x k ⋅ P { X = x k } E(X)=\sum\limits_{k=1}^∞x_k·P\{X=x_k\} E(X)=k=1∑∞xk⋅P{X=xk}
10.抽样分布定理
( n − 1 ) S 2 σ 2 \dfrac{(n-1)S^2}{σ^2} σ2(n−1)S2 = 1 σ 2 ∑ i = 1 n ( X i − X ‾ ) 2 = ∑ i = 1 n ( X i − X ‾ σ ) 2 =\dfrac{1}{σ^2}\sum\limits_{i=1}^n(X_i-\overline{X})^2=\sum\limits_{i=1}^n(\dfrac{X_i-\overline{X}}{σ})^2 =σ21i=1∑n(Xi−X)2=i=1∑n(σXi−X)2 ∼ χ 2 ( n − 1 ) \sim \chi^2(n-1) ∼χ2(n−1) 【17年18.】
11.泊松分布
P { X = k } = λ k k ! e − λ ( k = 0 , 1 , . . . ) P\{X=k\}=\dfrac{λ^k}{k!}e^{-λ} \quad (k=0,1,...) P{X=k}=k!λke−λ(k=0,1,...)
12.泊松积分
∫ − ∞ + ∞ e − t 2 d t = π \int_{-∞}^{+∞}e^{-t^2}dt=\sqrt{π} ∫−∞+∞e−t2dt=π、 ∫ 0 + ∞ e − t 2 d t = π 2 \int_{0}^{+∞}e^{-t^2}dt=\dfrac{\sqrt{π}}{2} ∫0+∞e−t2dt=2π
如何刷套卷
1.3h限时
2.熟悉会做的题先做,易得分的题先做
3.不空题,知道多少写多少
4.如何利用套卷提分?
查漏补缺,从失分的题中找分数
如考了90,则失了60分。目标是120分,还差30分。就从这丢的60分中找哪30分是经过努力可以拿到的分数,太难的就放过。【从丢掉的分数中找哪些分可以提高】
5.套卷不是刷得越多越好,比数量更重要的是质量。精刷,查漏补缺,真题要格外重视。在刷透真题的基础上,再刷模拟卷。
二、专业课
(一) 数据结构
1.算法题:
申请长度为n的辅助数组,并初始化为0
int *A = new int[n];
for(int i = 0 ;i < n; ++i) A[i] = 0;
算法题:
①给出数据结构类型的定义:单链表结点、二叉树结点
②要写函数名、所传参数,如 int Search_k (LinkList L, int k){ 【09年42.】
2.单链表结点的数据类型定义
typedef struct LNode{int data;struct LNode *next;
}LNode,*LinkList;
要表示一个单链表时,只需声明一个头指针L,指向单链表的第一个结点。
LinkList L;
使用LinkList:强调这是一个单链表
使用LNode *:强调这是一个结点
3.图 分类:无向图、有向图
无向边/边:(v , w) ,(m , n) 或 (w , v) , (n , m) 【17年(1)】
有向边/弧:<v , w> , <m , n>
4.合并有序表:
①最好:比较 min { m , n } \min\{m,n\} min{m,n}次
②最坏:比较 m + n − 1 m+n-1 m+n−1 次
5.结点数 = 1 + 度数 【16年42】
n 0 + n 1 + . . . + n k = 1 + 0 ⋅ n 0 + 1 ⋅ n 1 + . . . + k ⋅ n k n_0+n_1+...+n_k=1+0·n_0+1·n_1+...+k·n_k n0+n1+...+nk=1+0⋅n0+1⋅n1+...+k⋅nk
6.队列
(1)循环队列
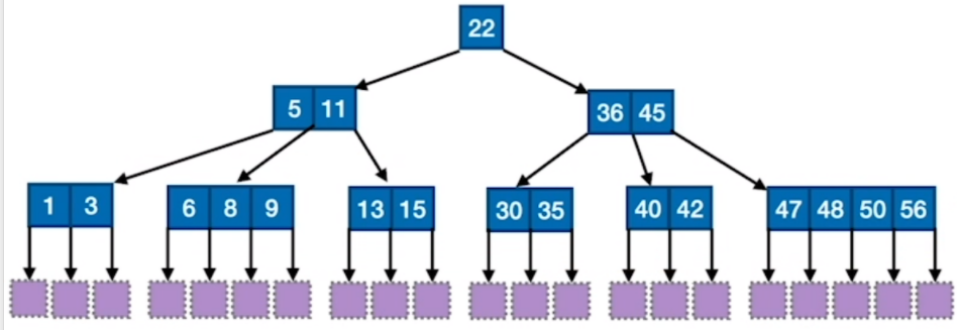
7.B树
(1)B树所有叶子结点都在同一层上 【09年8.】
(2)B树的阶就是子树的最大值m
(3)关键字永远比子树少1个,两棵子树中间夹一个关键字

8.外部排序
(1)最佳归并树:构造严格k叉树,需要补充的虚结点个数:k-1-u,u=(n-1)%(k-1)
(二) 计组
1.查页表在内存中的位置:
进程的PCB中有页表的起始地址,PCB将页表始址放到页表基址寄存器 PTBR中。
2.页表项地址 = 页表起始地址 + 页号×页表项长度
【其中页表项长度已知,只需要知道 页表始址 和 页号】
3.LA 逻辑地址:<虚拟页号,页内偏移量>
PA 物理地址:<物理页框号,页内偏移量>
4.二级页表:查页目录表(一级页表),由页目录号得到的物理页框号,是对应的二级页表存储的物理页框。在该页框中找到二级页表,再对比得到的物理页框号是页面所在的页框号。拼接得到页面的物理地址。
二级页表要查两次,但二级页表的TLB只查一次,对比的是完整的虚拟页号。
5.页面、页框 大小相等,页框是内存和磁盘之间数据交换的单位
主存块、Cache块 大小相等,块是内存和Cache之间数据交换的单位
6.Cache的三种映射的访存过程:
①全相联映射:高位均是Cache标记,直接查Cache标记
②直接映射:知道共有多少个Cache行,查行号,对比高位Cache标记是否匹配,有效位是否为1
③组相联映射:通过路数,求出共有多少组,查组号,对比高位Cache标记是否匹配,有效位是否为1
7.TLB只有全相联映射、组相联映射
8. 2 m 2^m 2m路组相联映射,有m bit LRU替换算法控制位
9.组相联映射:特定分组,组内任意位置。
映射的时候,每组只放一块,然后就轮到放下一组。【09年14.】
9.浮点数 ←→ 整数:
(1)int→float:当int的有效位大于24位时,int转float会丢失精度
(2)float→int:①当float表示的数,超过了int能表示的最大范围时,float转int会溢出 ②小数部分若丢失,也会丢失精度
10.溢出
(1)溢出判断:乘法指令【20年43.(4)②】
法一(符号):有符号数,若正数×正数=负数,则溢出
法二(表示范围):int型的表示范围 [-231,231-1],unsigned int型的表示范围 [0,232-1]
(2)用标志位判断溢出
OF = 1:带符号数溢出
CF =1 :无符号数溢出
(3)移位运算导致的溢出:无符号数移位不会溢出,只有带符号数移位才可能因为符号位变化产生溢出 【14年45(3)】
11.2n-1 的二进制表示为 n个1
12.左规(向左规格化):小数点不动,整体右移一位,阶码+1
右规(向右规格化):小数点不动,整体左移一位,阶码-1
13.移位运算:
左移1位 ⇔ \Leftrightarrow ⇔ 乘2
右移1位 ⇔ \Leftrightarrow ⇔ 除2
算数移位:带符号数
逻辑移位:无符号数
14.IEEE754 表示 (特殊情况)
(1)移码为255,尾数全0: + ∞ +∞ +∞或 − ∞ -∞ −∞ (正负看符号位)
(2)移码为0,尾数全0:+0 或 -0
(3)移码为255,尾数非0:NaN
(4)移码为0,尾数非0:非规格化数
15.函数调用的机器级表示:
(1)访问局部变量:
①定义的第一个局部变量:[ebp - 4]
②定义的第二个局部变量:[ebp - 8]
③定义的第三个局部变量:[ebp - 12]、[ebp - 0CH]
(2)访问函数调用的参数 (函数括号内的传递参数):
①第一个参数:[ebp+8]
②第二个参数:[ebp+12]
16.标志位的生成:
(1)CF = Cn⊕sub 【Cn为最高位的进位。加法sub=0,减法sub=1。异或是模二加法】
CF = 1 表示 无符号数溢出
17.计组 09-15年是唐朔飞老师命题,偏硬件。16-23年是袁春风老师命题,软件结合,没有那么硬了。
注释,打 [ ]是袁版,打()是唐版
18.短变长:先扩展,再解释:
无符号整数:零扩展
带符号整数:符号扩展
【A类型→B类型要扩展,是按原来类型A类型进行扩展】
19.x86特性:
①x86 所有的转移指令都是 相对寻址 (MIPS的转移指令也是相对寻址):转移指令的后一条指令的起始地址 + 偏移量 = 转移的目的地址,求偏移量 【2014年44.】
②x86的存储方式是 小端存储 (可以用所给数的16进制验证) 【2023年44.】
20.地址计算:长的地址 + 短的偏移量(补码/带符号整数):短的偏移量先进行符号扩展,再相加 【2013年44.(2)①】
21.条件转移指令向后跳转:向后是指地址增大 【2013年44.(1)】
22.指令异常:
(1)指令溢出:溢出是算术运算的现象。无符号数移位不会溢出。 【2014年45.(3)①】
(2)指令缺页:只有访存指令(load、store)可能产生缺页异常 【2014年45.(3)②】
23.Cache缺失次数:只和访存次数有关,与指令没有直接关系,所以要看每条指令的平均访存次数【2013年(4)】
24.指令Cache缺失率:每次执行指令,要先取指令,要访存。也就是先访问指令Cache,看其中有没有要执行的指令。 【2014年45.(2)】
25.从Cache中访问指令的过程、组相联映射的Cache缺失的处理过程 【20年(3)】
(2)Cache缺失处理过程:将 xxxxx(主存块号) 主存块整块放入Cache第x组的任意一行。将Cache行标记设为xxx(主存字块标记tag),有效位置为1,并修改LRU位。根据块内地址 xxx 从Cache行中取出指令字。
26.(1)Cache总容量 = 标记项容量 + 数据区容量 = Cache块数×(标记项 + 数据)
标记项 = ①tag + ②有效位 + ③脏位(一致性维护位) + ④LRU替换算法控制位
(2)Cache数据区容量 = Cache块数× 每块大小(数据) 【2014年45.(2)】
27.CPU访问主存的过程:
①将逻辑地址转换为物理地址:先查TLB,TLB不命中再查页表,页表不命中则缺页中断,访问磁盘。然后重新访问TLB,进行虚实地址转换。
②根据物理地址读取数据:先访问Cache,Cache不命中则访问主存。

28.寄存器:
(1)MAR位数 = 地址线根数,MDR位数 = 数据线根数,可寻址主存空间大小 = 2MAR位数×编址单元
(2)指令寄存器IR:
①作用:存放当前指令
②IR位数 = 指令字长 【若指令为不定长,则IR位数 = 最长的指令的位数】
(3)ALU宽度 = 机器字长
29.n位补码可表示的范围:-2n-1 ~ 2n-1-1
8位补码可表示的范围:-27 ~ 27-1 ,即 -128 ~ 127
30.RISC与CISC
(1)RISC大多数指令在一个时钟周期内完成 【09年17.】
(2)RISC的内部寄存器数量相对CISC多 【09年17.】
(3)RISC采用硬布线控制器,特点是:指令执行速度快,指令功能的修改和扩展困难【09年19.】
31.带符号整数加/减运算、无符号正数加/减运算,能利用同一个加法器辅助电路实现的理由:【11年43(3)】
①加法器只负责对二进制数进行计算并产生标志,运算前并不区分有无符号。
②加法a+b可用加法器直接实现。减法a-b = a + [-b]补可转化为加法进行计算。[-b]补为[b]补全部按位取反,再加1。
32.无符号整数加/减运算的结果溢出判断:
①OF = Cn⊕Cn-1 = 1,即加法器完成加法操作时,最高位的进位和次高位的进位不同,则无符号整数溢出
②加法器两个输入端的符号相同,但输出结果(和)与其符号不同
带符号整数加/减运算的结果溢出判断:CF = Cn⊕sub = 1 (加法sub = 0,减法sub = 1)
(三) 操作系统
1.开中断指令与关中断指令都是特权指令,只能在核心态下执行,不能在用户态下执行。故用户程序不能使用开/关中断指令。
2.PV操作:
(1)读者-写者问题:读读不互斥,读写、写写互斥
3.页表的最大长度:页表项数×页表项大小 = 2 页号位数 2^{页号位数} 2页号位数×页表项大小 【13年大题】
4.可用 “无符号右移 <<<” 和 “按位与 &” 操作,取出某几个二进制位的值
【13年大题】
页目录号的表达式:(LA>>>22) & 0x3FF
页号的表达式:(LA>>>12) & 0x3FF
5.访问虚拟地址的时间:【09年大题】
①映射为物理地址的时间:访问TLB、访问页表、处理缺页+重新访问TLB
②访问内存的时间
6.操作系统关心的是文件的物理结构(文件分配方式):连续分配、链接分配、索引分配
①连续分配方式中,FCB的内容:
文件名、文件起始块号、文件长度
7.文件系统:
①UFS文件系统:Unix操作系统的文件系统,使用索引结点 inode【在Unix⽂件系统中,每个⽂件的目录项对应⼀个inode结点,而inode结点的总数是有上限的(inode区大小 / inode结点大小 = inode个数),故该文件系统能存储的文件个数也有上限。】
②FAT文件系统:显式链接。文件分配表FAT固定存储在磁盘的某个块中。开机时就去该固定位置将整个FAT读入内存
③NTFS文件系统:Windows的磁盘文件系统
FAT32、NTFS、exFAT
8.文件目录的两种实现形式:
①每一个目录项:一个完整的FCB
②每一个目录项:文件名 + 索引结点编号 (inode结点:存除文件名外的其他信息 + 混合索引表)
在Unix文件系统UFS中,索引节点inode固定地集中存放在连续的某几个块,称为inode区,是一个数组。任何一个文件都对应一个索引结点。
9.访问某个文件的过程:
①根据目录文件,将inode读入内存
②根据inode中的混合索引表,将文件所在的磁盘块读入内存
10.索引结点:
①存放在磁盘分区的固定位置,磁盘块号是固定的:inode区
②每个索引结点(inode结点)的大小是固定的。可以通过inode区起始块号 + 索引结点的编号,随机存取某指定编号的索引结点
11.文件采用连续分配方式的优点:
磁盘寻道时间短,支持随机访问,效率高 【11年46.(1)】
12.FCB集中存放的优点:
随机查找文件名时,只需访问FCB对应的磁盘块。可减少磁盘I/O次数、磁头移动次数 【11年46.(2)】
(四) 计网
1.曼彻斯特编码:
以太网采用曼彻斯特编码,曼彻斯特编码的数据率:波特率一半
若以太网波特率为40MBaud,则数据率为:20Mb/s
2.基带、宽带(频带)
基带信号:将数字信号1和0直接用两种不同的电压表示,然后送到数字信道上传输 (基带传输)
宽带信号:将基带信号进行调制后形成频分复用模拟信号,然后送到模拟信道上传输 (宽带传输、频带传输)
3.编码与调制
编码:→数字信号
调制:→模拟信号
4.各层的主要功能:
①LLC子层:给高层提供服务与接口、建立和释放数据链路层的逻辑连接、差错控制、给帧加序号
②MAC子层:组帧和拆帧、比特差错检测、寻址
③物理层:信号的编码和译码、比特的接收与传输
LLC子层的作用:给帧加序号
5.曼彻斯特编码:速度传输率是码元传输率的一半
6.10Base T ,Base是指基带传输,数字信道
7.Internet和internet:
①Internet是因特网,internet是互联网
②因特网是最大的互联网
③广域网再大,仍然是单一网络。而互联网是多个网络互联。[∴因特网(多个网络互联)比最大的广域网(仍然是一个网络)更大,因为还互联了一些小的。]
8.报文段-IP数据报/IP分组-数据MAC帧-比特流
9.PPP协议,不可靠、不编号、不确认
10.以太网的特点(9个)
(1)以太网MAC帧的数据部分:46B~1500B
①进行填充:小于46B (2EH)
②进行分组:大于1500B
46B=2EH,若IP数据报总长度不足46B=2EH,则经过快速以太网传输时需要进行填充 [2012年(1)③]
11.交换机的自学习算法:无对应转发表表项,则会向除源端口外的其他端口广播 。并将来源MAC地址和端口写入转发表。
12.片偏移,每个分片大小是8B的整数倍。指的是分片的数据部分大小是8B的整数倍,不是加了首部后分片的总长度。
13.与255相与,值不变。与0相与,全为0。不必写成二进制进行与运算,可以简化计算。
14.TCP拥塞控制:
若下次翻倍后会超过门限值ssh,则取门限值作为下一轮的拥塞窗口大小,即 cwnd=ssh;
例如:门限值是6,则接收窗口变化应当是:1-2-4-6-7-8-9-…
15.使用UDP数据报封装的应用层协议:DNS、RIP
使用TCP封装的应用层的协议:BGP、FTP、SMTP、HTTP
16.主机和本地域名服务器中有高速缓存,可能存储了要访问的网站的域名与IP地址的映射,就不必再发出DNS查询请求。
17.GBN:累计确认:回复ACKn,则代表n及n以前的都正确接收
SR:没有累计确认的特性。一个一个确认。
18.数据链路层的滑动窗口 和 TCP的滑动窗口的区别:TCP的滑动窗口大小可变,而数据链路层的滑动窗口是固定死的,大小不可变。
19.主机封装DHCP发现报文的IP分组的源IP地址和目的IP地址?
源IP地址:0.0.0.0;目的IP地址:255.255.255.255
20.IP组播的MAC地址:
前24位 01-00-5E + 第25位是0 + 后23位用IP地址代替
21.HTTP 持久连接 非流水线方式:TCP连接建立后不断开,传web页面一个RTT,传每个元素一个RTT
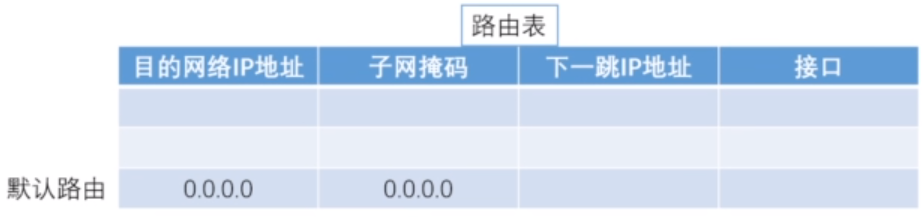
22.路由表表项:[目的网络IP地址,子网掩码,下一跳IP地址,接口 ]
默认路由的目的网络IP地址和子网掩码 都是 0.0.0.0
23.TCP连接建立过程中,从哪一次开始可以发送数据?
第三次握手 时可以携带数据。
24.网络 vs 网段
①网络:同一个广播域,路由器的同一个端口 + 子网掩码与网络号相与的结果相同 【同一个广播域,同一个路由器端口,不一定是同一个网络,可能接错了。如16年39.】
跨网络,则MAC地址发生变化。
②网段:同一个冲突域,交换机的同一个端口
25.MTU指该网段限制的数据部分的最大长度,不包含首部+尾部。
IP数据报的片偏移字段:仅指数据部分的偏移
27.生存时间TTL:是减去经过的路由器个数,而不是链路费用 (路径长度)
29.确认帧总由数据帧捎带,则计算信道利用率时, t 2 = t 1 t_2=t_1 t2=t1, T = t 1 + R R T + t 2 T=t_1+RRT+t_2 T=t1+RRT+t2
30.TCP流量控制:
seq、ack:以字节为单位 【16年(3)】
31.TCP报文段、IP数据报、MAC帧的题目:
(1)第一步,①将IP地址翻译为16进制,找到对应位置;②MAC地址找到对应位置。
(2)TCP首部长度:数据偏移字段,以4B为单位
(3)UDP数据报的总长度:以1B为单位。UDP首部为8B。
32.数据传输率的单位:将KB/s 化成 b/s,kb/s,Mb/s 【16年(3)②】
33.浏览器访问某域名所经历的详细过程:【2021年(2)(3)】
①DNS→IP地址:递归查询/迭代查询
②IP地址→MAC地址:ARP表有则直接转换。没有,则 ARP请求分组(广播)→,ARP响应分组(单播)←
③TCP连接建立 (三次握手)
④HTTP请求:html页面 + 图像等元素
34.十六进制→二进制→十进制的转换:
A = 10 = 1010B
B = 11 = 1011B
C = 12 = 1100B
D = 13 = 1101B
E = 14 = 1110B
F = 15 = 1111B
35.线路效率 = 吞吐率 信道带宽 \frac{吞吐率}{信道带宽} 信道带宽吞吐率
36.100Base-T:100Mb/s
37.套接字 Socket = (主机IP地址,端口号)
38.最小帧长 = RTT×数据传输率
以太网帧的最小帧长:64B
39.若有nbit主机号,则:
(1)总可用的主机IP地址个数为: 2 n − 2 2^n-2 2n−2
n n n位主机号,则可分配的主机IP地址有 2 n − 2 2^n-2 2n−2 个。(减去主机号全0的本网络、主机号全1的广播地址)【10年37.】
(2)还可分配的主机IP地址个数为: 2 n − 2 − 2^n-2- 2n−2−已分配的主机数 − - −已分配的路由器端口数
40.若A到B要经过多条链路,记得 每条链路都有发送时延(传输时延)
41.数据交换方式:
(1)报文交换:报文交换耗时为整数,总耗时长
(2)分组交换:分组交换,链路上有n个路由器,则多n个零头。总耗时短
42.要构造以太网数据帧时,用什么协议确定目的MAC地址? 【11年47.(2)】
ARP协议
每台主机都设有一个ARP高速缓存,用来存放本局域网上各主机和路由器的IP地址到MAC地址的映射表,称ARP表。以目的IP地址对照ARP表,若有对应MAC地址,则用该MAC地址作为目的MAC地址。若没有,则广播 ARP请求分组 FF-FF-FF-FF-FF-FF
咸鱼学长传记
咸鱼传记:
1.张鸿林,1994年生,云南普洱人,少数民族。15年大学毕业,18年二战考入北大软微(24岁),做操作系统。
2.本科:北京理工大学-软件工程,2012-2015。大学期间很浪,三个舍友都出国留学了,自己只能去打工。2015年毕业做java手游开发(不良人),月薪1w,年薪12w,但当时手游大火,年终奖发了24w。工作了一年很迷茫打算考研。
3.一战:16年8月辞职,复习了4个多月,没考上。一战数学56分,英语57分
4.二战:工作的钱花光了,不好意思向家里要钱,打算边工作边考研。被老父亲制止,说目光要放长远,目标是要考上研而不是省钱。脱产复习了一年,报了数学线下班,中间周期性焦虑,觉得自己考不上。
上考场时的复习进度:①408:只做了真题,单科书大题只做了一半。②数学:真题做了06-17年
5.二战成绩:①软微自命题:143 ②数学:117 ③英语:58 ④政治68 总分:386。二战上岸北大软微
6.入学前,风华招人兼职讲操作系统。发现还蛮喜欢讲课,就正式进入了王道。
7.喜欢音乐,初始时以五月天的《咸鱼》命名了自己的网名。
三、英语
(一) 完型
(二) 阅读
看题型:细节题、主旨题、推断题。答案都在文中能找到出处。
(三) 新题型
1.行文思路:①现象 → ②问题 → ③原因 →④解决方案 【13年新题型(七选五)】
2.段首、段尾、空前、空后
①小标题—段落中心
②排序题-关注首尾逻辑
③七选五-关注上下句逻辑:
3.排序首段:注意倒装句
In his 1936 work How to Win Friends and Influence People, Dale Carnegie wrote:…
该句的his是指代Dale Carnegie,是倒装句,句内指代。而不是指代上文。
4.末段作用:总结全文、点明主旨、深化中心、呼应开头、发出呼吁
(四) 翻译:划分句子成分
1.时间状语提至句首
2.注意不要将 短小的后置定语 错认为是主句的谓语和宾语。【15年:immigrants (bound for territory) crossed the Atlantic.】
1.谢一帆8分步骤:
不要直接写,先打草稿
①一个一个小短句写下来,按照顺序组起来
②根据文义把某些单词的意思改写,即意译
晶婷老师:前期训练需要先打草稿调整,只有训练的多了,考场上才能不打草稿直接出答案。
2.技巧:
①增译、删译
②补充主语
③根据语境,将某些单词的词意进行意译
④定语从句,可以拆分成两个句子。该名词在前一小句中作宾语,在后一小句中作主语。
3.中文和英文思维方式的区别:
①中文多主动,英文多被动
②中文多重复,英文多省略
③中文多短句,英文多长句
④英文定状后置,中文定状前置。(时间状语、地点状语前置)
(五) 作文
整理优秀的、通用的句子。分为 段首、段中、段尾,分别都要整理句子。
(1)小作文:书信为主:模板+结合题目
(2)大作文:英一图画:模板+扣题句
学习方法
1.学累了的休息方式:4s
①speak:和同学交流复述学过的内容 (费曼学习法)
②switch:学累了就换一科,大脑就能得到休息
③sports:运动。能增加神经元数量
④sleep:睡觉时大脑会处理废物,组织信息,加强记忆。 (空卡建议:睡前30分钟复习,别看手机)
2.学习感悟
1.学习的本质是重复,是温故而知新
2.实在不会做,照着答案边做边抄。抄一遍,效果会很好。【不会做,就照答案抄。抄着抄着就有感觉了】对于完全没有思路的题,只用眼睛看两遍答案是学不会的,过一周就全忘记了。得抄写答案的解答过程。
3.看起来越难的东西,其实考的越简单,套路越少。
看起来越简单的东西,其实考的越难,套路很多。
3.对抗焦虑