目录
1. Transform.Rotate 方法
使用
2. Transform.rotation 或 Transform.localRotation 属性与四元数
使用方式:
小案例 :目标旋转角度计算:targetRotation(Quaternion类型)
玩家发现敌人位置,玩家转向敌人的实现
3. Quaternion.LookAt 或 Transform.LookAt 方法
使用方式:
4. Quaternion.Euler 方法
使用方式:
5. 插值方法(如 Quaternion.Lerp 和 Quaternion.Slerp)
使用方式:
插值的拓展:
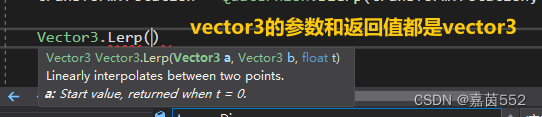
vector3.lerp()
vector3.erp()
Quaternion.Lerp()
Quaternion.Slerp()
区别:
Quaternion的返回值和参数都是Quaternion
编辑
Vector3的返回值和参数都是Vector3编辑
6.以上旋转区别与总结
案例
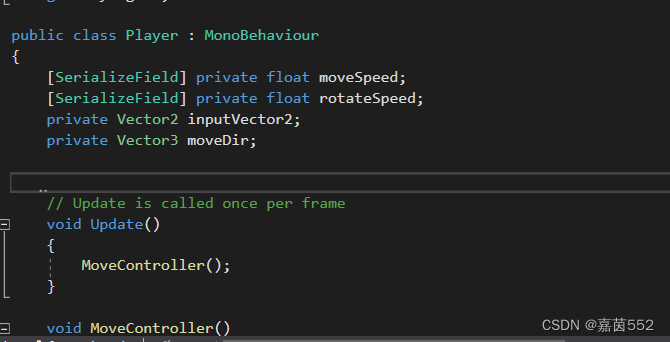
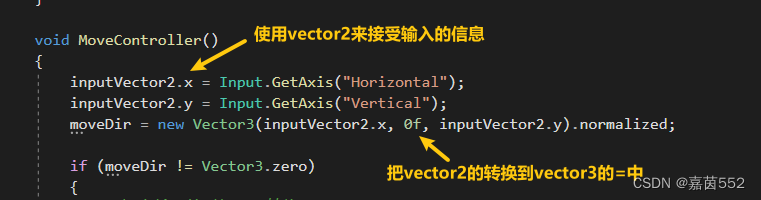
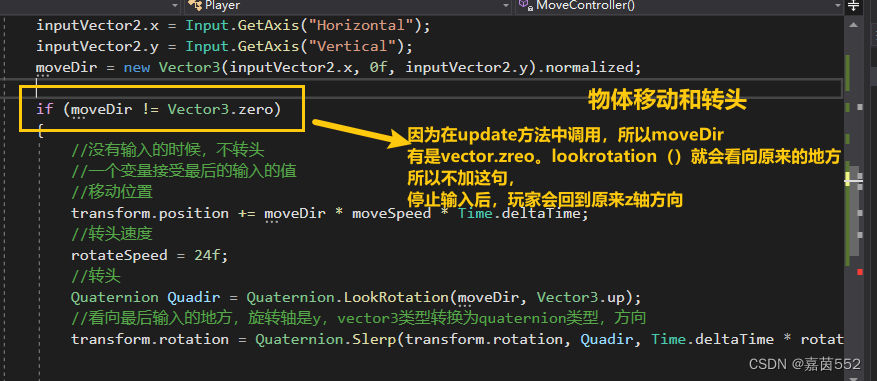
玩家通过输入来实现移动和转头
transform.rotation = 类型是 四元数
transform.eularAngle =
transform.LookAt () 类型是 vector3
平滑的插值--------------------
slerp lerp
vector3.slerp(vector3 a,vector3.b,float t); 意思是从a点到b点旋转时候,时间t
Quaternion.Lerp (quaternion类型,quaternion类型,float);
1. Transform.Rotate 方法
使用
transform.Rotate(Vector3.up * speed * Time.deltaTime);
描述:Rotate 方法直接对物体的本地坐标系应用旋转。它接受一个Vector3参数,表示沿X、Y、Z轴的旋转角度(以度为单位)。也可以接受一个额外的参数来指定旋转是在世界坐标系还是本地坐标系中进行。
特点:
- 直观易用,适用于简单的旋转需求。
- 由于是直接对角度进行累加,长期旋转可能导致数值不稳定或漂移。
2. Transform.rotation 或 Transform.localRotation 属性与四元数
Transform.rotation= quaternion类型Quaternion.Lerp (quaternion类型,quaternion类型,float)
//返回的是quaternion类型 //参数也是quaternion类型
使用方式:
Quaternion targetRotation = Quaternion.Euler(90, 0, 0);
transform.rotation = targetRotation; //接受的是四元数或者
Quaternion newRotation = Quaternion.Lerp(transform.rotation, targetRotation, Time.deltaTime * rotationSpeed); //四元数插值(本身的旋转角度,目标旋转角度,时间)
transform.rotation = newRotation;
小案例 :目标旋转角度计算:targetRotation(Quaternion类型)
Quaternion.LookRotation ( ve3-ve3);//返回的是Quaternion
Quaternion.Lerp()//参数(Quaternion,Quaternion,float)//返回值Quaternion
玩家发现敌人位置,玩家转向敌人的实现

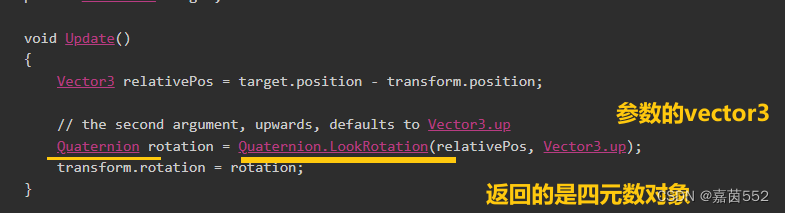

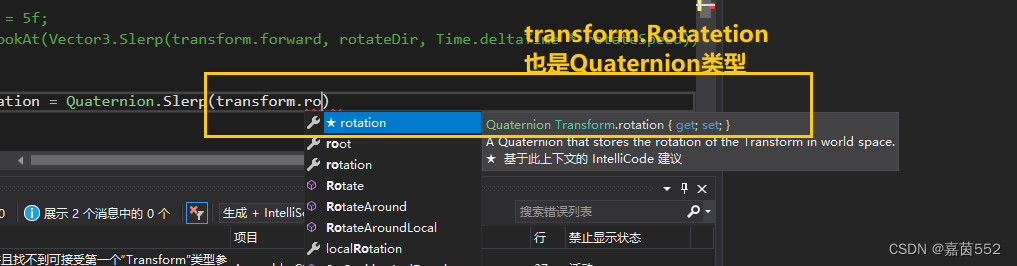
描述:
rotation 和 localRotation 属性分别表示物体在世界坐标系和本地坐标系中的旋转,它们都是Quaternion类型。可以使用四元数运算来平滑地插值或组合旋转。
特点:
- 四元数运算可以提供更稳定和平滑的旋转。
Lerp、Slerp等插值方法可以用于实现平滑过渡。- 需要对四元数有一定的理解才能正确使用。
3. Quaternion.LookAt 或 Transform.LookAt 方法
使用方式:
Quaternion targetRotation = Quaternion.LookAt(transform.position, target.position, Vector3.up); transform.rotation = targetRotation;或者
transform.LookAt(target.position);//敌人的位置 vector3类型
描述:
这些方法使物体朝向指定的位置或目标。Quaternion.LookAt返回一个四元数,表示从当前位置朝向目标位置的旋转;Transform.LookAt则直接应用这个旋转到物体的rotation属性上。
特点:
- 适用于让物体朝向特定目标的情况。
Transform.LookAt更简洁,但不如使用四元数灵活。
4. Quaternion.Euler 方法
使用方式:
Quaternion rotation = Quaternion.Euler(xAngle, yAngle, zAngle);
transform.rotation = rotation;
描述:
Quaternion.Euler 方法根据欧拉角(以度为单位)创建一个四元数。欧拉角是表示三维旋转的一种方式,由绕X、Y、Z轴的三个角度组成。
特点:
- 可以将欧拉角转换为四元数,方便进行旋转操作。
- 需要注意欧拉角的旋转顺序,不同的顺序可能导致不同的结果。
5. 插值方法(如 Quaternion.Lerp 和 Quaternion.Slerp)
使用方式:
Quaternion newRotation = Quaternion.Slerp(startRotation, endRotation, t);
transform.rotation = newRotation;
插值的拓展:
vector3.lerp()
vector3.erp()
Quaternion.Lerp()
Quaternion.Slerp()
区别:
Quaternion的返回值和参数都是Quaternion
Vector3的返回值和参数都是Vector3
描述:
Lerp(线性插值)和Slerp(球面线性插值)用于在两个四元数之间平滑过渡。它们接受起始四元数、结束四元数和一个插值因子t(范围在0到1之间),并返回一个新的四元数。
特点:
- 可以实现平滑的旋转过渡效果。
Slerp通常比Lerp更适合用于旋转插值,因为它考虑了旋转的最短路径。
6.以上旋转区别与总结
Transform.Rotate方法简单直观,但长期旋转可能导致数值不稳定。- 使用四元数和插值方法(如
Slerp)可以实现更稳定和平滑的旋转效果,但需要一定的数学基础。 Transform.LookAt和Quaternion.LookAt适用于让物体朝向特定目标。Quaternion.Euler可以将欧拉角转换为四元数进行旋转。
在选择使用哪种方法时,应根据具体需求、旋转的复杂性和性能要求来权衡。
对于简单的旋转,
Transform.Rotate可能足够;而对于需要平滑过渡或精确控制的旋转,使用四元数和插值方法可能更合适。
案例
玩家通过输入来实现移动和转头