一、整式

1. 同底数幂的乘法

公式：$a^m\ast a^n=a^{m+n}$

例：$a^3\ast a^2=a^{3+2}=a^5$

2. 幂的乘方

公式：$(a^m{)}^n=a^{m\ast n}$

例：$(a^2{)}^6=a^{2\ast 6}=a^{12}$

3. 积的乘方

公式：$(ab{)}^n=a^n\ast b^n=a^n{b}^n$

例：$(ab{)}^5=a^5\ast b^5=a^5{b}^5$

4. 乘法分配律

公式：$a\ast (b+c)=ab+ac$

例：$2x\ast (3x+y)=2x\ast 3x+2x\ast y=6x^2+2xy$

5. 同底数幂的除法

公式：$a^m÷a^n=a^{m-n}$

例：$6a^4{b}^{2}c÷2a^{2}b=3a^{4-2}{b}^{2-1}{c}^{1-0}=3a^{2}bc$

二、分式

1. 分式的乘法

公式：$\frac{b}{a}\ast \frac{d}{c}=\frac{b\ast d}{a\ast c}$

例：$\frac{1}{3}\ast \frac{2}{3}=\frac{1\ast 2}{3\ast 3}=\frac{2}{9}$

2. 分式的除法

公式：$\frac{b}{a}÷\frac{d}{c}=\frac{b}{a}\ast \frac{c}{d}$

例：$\frac{1}{3}÷\frac{2}{3}=\frac{1}{3}\ast \frac{3}{2}=\frac{3}{6}=\frac{1}{2}$

3. 分式的乘方

公式：$(\frac{b}{a}{)}^n=\frac{b^n}{a^n}$

例：$(\frac{2}{3}{)}^2=\frac{2^2}{3^2}=\frac{4}{9}$

4. 分式的最简公分母

最简公分母就是找到多个分式间的公分母，在分式加减和分式方程化简时会使用。

分式加减时，当异分母相加减时，需要先找到最简公分母进行通分，然后在进行分子的加减

分式方程化简时，需要先找到最简公分母，然后对分式进行化简，也就是利用最简公分母去掉分式的分母，最后再计算

找到最简公分母的规则：

1. 当所有分式都是单项式时：

(1) 找到所有分式的分母中的单项式的系数，然后取它们的最小公倍数

(2) 将所有分式的分母中的单项式的字母都罗列出来，当有字母相同时，留下次数高的

(3) 将最小公倍数和留下的字母进行拼接，就是最简公分母

2. 当分式中有多项式时，先判断多项式能否因式分解，能分解则先分解，不能分解就把整个多项式想象成单项式中的一个字母，然后再按照单项式的规则找到最简公分母

下面分别用单项式和多项式举例：

单项式，分式加法，例：

$$\begin{gathered} \frac{1}{3a^{2}bc}+\frac{1}{2a{b}^2} \\ =两个分式中分母的系数分别是3和2，所以它们的最小公倍数是6 \\ =两个分式中分母的字母有：a、b、c，遇见相同字母留下最高次数的字母，所以是a^2{b}^{2}c \\ =将最小公倍数和留下的字母进行拼接，得到最简公分母：6a^2{b}^{2}c \\ =然后让两个分式的分母都变成6a^2{b}^{2}c \\ =\frac{1}{3a^{2}bc}\ast \frac{2b}{2b}=\frac{2b}{6a^2{b}^{2}c} \\ =\frac{1}{2a{b}^2}\ast \frac{3ac}{3ac}=\frac{3ac}{6a^2{b}^{2}c} \\ =\frac{2b}{6a^2{b}^{2}c}+\frac{3ac}{6a^2{b}^{2}c}=\frac{2b+3ac}{6a^2{b}^{2}c} \end{gathered}$$

多项式，分式方程化简，例：

$$\begin{gathered} 2\ast \frac{8000}{x}=\frac{17600}{x+4} \\ =两个分式的分母分别是单项式x和多项式x+4，先判断x+4能否分解 \\ =x+4不能分解，那么就把x+4想象成单项式中的一个字母，然后套用单项式的规则找到最简公分母 \\ =两个分式中分母x和x+4的系数都是1，所以最小公倍数就是1 \\ =两个分式中分母的字母有：x、x+4，并且没有相同的字母，所以留下x和x+4 \\ =将最小公倍数和留下的字母进行拼接，得到最简公分母：1(x)(x+4)=x(x+4) \\ =得到最简公分母后就可以对分式方程进行化简 \\ =\frac{8000}{x}\ast x(x+4)=8000(x+4) \\ =\frac{17600}{x+4}\ast x(x+4)=17600x \\ =将两个化简后的分式带回到方程中 \\ =2\ast 8000(x+4)=17600x \\ =16000(x+4)=17600x \\ =16000x+64000=17600x \\ =x=40 \end{gathered}$$

5. 负指数幂

公式：$n^{-m}=\frac{1}{m^n}$

例：$5^{-5}=\frac{1}{5^5}$

6. 比例变形

公式：$\frac{b}{a}=\frac{d}{c}可变形为cb=ad，同理cb=ad也可变形为\frac{b}{a}=\frac{d}{c}$

例：$\frac{x}{y}=\frac{3}{2}，2x=3y$

公式：$a÷b÷c=\frac{a}{bc}$

例：$6÷3÷2=\frac{6}{2\ast 3}$

7. 分离常数法

用拆项使分式的分子为常数

例：

$\frac{x+2}{x+1}=\frac{x+1+1}{x+1}=\frac{x+1}{x+1}+\frac{1}{x+1}=1+\frac{1}{x+1}$

三、二次根式

0. 平方根和算数平方根的重要概念

一个数小于 $0$ 时，它没有平方根，算式是错误的，不成立，没意义。

一个数等于 $0$ 时，它只有一个平方根，就是 $0$

一个数大于 $0$ 时，它有两个平方根，分别是 $\sqrt{x}$ 和 $-\sqrt{x}$，其中 $\sqrt{x}$ 叫做 $x$ 的算数平方根

如果题中是求 a 的平方根，这个时候 $a$ 是有两个平方根的，分别是 $\sqrt{a}$ 和 $-\sqrt{a}$，这两个叫做 $a$ 的平方根。如果题中是求 $\sqrt{a}$，这时候其实只要求出 $\sqrt{a}$ 就可以，这个叫做算术平方根，千万千万不要弄混，例如： 如果题目是求 $9$ 的平方根，那么 9 有两个平方根，分别是 $\sqrt{9}$ 和 $-\sqrt{9}$，结果是 $\pm 3$。如果题目是求 $\sqrt{9}$ ，这时候让求的不是 9 的平方根，而是 9 的算术平方根，结果就是 3

1. 乘方去根号

${\sqrt{a}}^2=a，\sqrt{a^2}=|a|$

例：${\sqrt{3}}^2=3，\sqrt{-3^2}=|-3|$

2. 二次根式的加减

二次根式的加减需要满足两个根式是同类二次根式，也就是根号下的数值必须是一样的

减法：$3\sqrt{a}-2\sqrt{a}=\sqrt{a}$

加法：$\sqrt{a}+\sqrt{a}=2\sqrt{a}$

例：$\sqrt{3}+\sqrt{3}=2\sqrt{3}$

3. 二次根式的乘法

$\sqrt{a}\ast \sqrt{b}=\sqrt{a\ast b}$

例：$\sqrt{2}\ast \sqrt{3}=\sqrt{2\ast 3}=\sqrt{6}$

4. 二次根式的除法

$\frac{\sqrt{a}}{\sqrt{b}}=\sqrt{a}÷\sqrt{b}=\sqrt{\frac{a}{b}}$

例：$\frac{\sqrt{2}}{\sqrt{3}}=\sqrt{2}÷\sqrt{3}=\sqrt{\frac{2}{3}}$

5. 二次根式的化简

二次根式的化简有二个原则：

1. 能开出来的，必须开出来
   找到根号下数值的所有自身以外的因数，判断因数能否开根，能开根则就要对这个二次根式进行化简
   例：
   $\sqrt{6}，其自身以外的因数是2\ast 3，\sqrt{2}、\sqrt{3}都不能开根，所以\sqrt{6}无法化简$
   $$\begin{gathered} \sqrt{18}，其自身以外的因数有3\ast 6和2\ast 9，\sqrt{3}、\sqrt{6}不能开根， \\ 所以就得试另一组因数\sqrt{2}、\sqrt{9}，因为\sqrt{9}可以被开根，其开根后的算数平方根是3， \\ 所以\sqrt{18}是可以被化简的，其化简后为\sqrt{2\ast 9}=\sqrt{2}\ast \sqrt{9}=3\sqrt{2} \end{gathered}$$

2. 根号里不能有分母，分母里不能有分号
   公式：
   $\sqrt{\frac{b}{a}}\to \sqrt{\frac{b}{a}}\ast \sqrt{\frac{a}{a}}=\frac{\sqrt{b}\ast \sqrt{a}}{\sqrt{a}\ast \sqrt{a}}=\frac{\sqrt{ab}}{\sqrt{a^2}}=\frac{\sqrt{ab}}{a}$

   例：
   $\sqrt{\frac{2}{3}}\to \sqrt{\frac{2}{3}}\ast \sqrt{\frac{3}{3}}=\frac{\sqrt{2}\ast \sqrt{3}}{\sqrt{3}\ast \sqrt{3}}=\frac{\sqrt{6}}{\sqrt{9}}=\frac{\sqrt{6}}{3}$

6. 有理化

有理化是在一些特定场合中，需要将式子中无法直接化简的根号去掉，以便于计算，需要多刷题才能有感觉

举个代入式的例子：

$$\begin{gathered} x=\frac{4+3\sqrt{5}}{2}，求8x(x-4)得多少？ \\ 移项：2x=4+3\sqrt{5} \\ 移项：2x-4=3\sqrt{5} \\ 有理化：(2x-4{)}^2=(3\sqrt{5}{)}^2 \\ 左边的式子利用平方差公式后为：4x^2-16x+16=45 \\ 左边的式子再提取公因式为：4x(x-4)=29 \\ 然后带入到要求的式子里：8x(x-4)=2\ast 4x(x-4)=29\ast 2=58 \end{gathered}$$

再举个分母有理化的例子：
$$\begin{gathered} \frac{1}{\sqrt{3}-\sqrt{2}} \\ 想让分母不包含根式，我们需要对分母进行乘方， \\ \frac{(1{)}^2}{(\sqrt{3}-\sqrt{2}{)}^2}，然后利用完全平方公式展开，\frac{1}{3-2\sqrt{6}+2}，会发现结果还有根式 \\ 所以这里不适合对整个分母进行乘方，可以让其分别乘方，变成{\sqrt{3}}^2-{\sqrt{2}}^2， \\ 仔细观察这就是平方差公式，所以： \\ \frac{1\ast (\sqrt{3}+\sqrt{2})}{(\sqrt{3}-\sqrt{2})(\sqrt{3}+\sqrt{2})}=\frac{\sqrt{3}+\sqrt{2}}{{\sqrt{3}}^2-{\sqrt{2}}^2}=\sqrt{3}+\sqrt{2} \end{gathered}$$

四、因式分解和解一元二次方程的相关内容

因式分解公式：提取公因式、平方差公式、立方和公式、立方差公式、完全平方公式、首一十字相乘、非首一十字相乘

解一元二次方程的公式：配方法、直接开平方、公式法

因式分解的本意是将多项式变为整式乘积的一个过程，但是这个过程中可以解开一些一元二次方程，所以因式分解的这些公式，有时候也可以用来解一元二次方程

1. 提取公因式

找到多项式中公共的因式并提取出来，公式：$a\ast b+a\ast c=a\ast (b+c)$

例：$2x^{2}y+6x{y}^2=2xy\ast (x+3y)$，两个多项式的公共因式：$2xy$

2. 平方差公式

公式：$a^2-b^2=(a+b)(a-b)$

例：
$$\begin{gathered} a{x}^2-9a \\ =a\ast (x^2-9)（先用提取公因式的方式，提取两个多项式的公共因式a） \\ =a\ast (x^2-3^2)（x^2-3^2满足平方差公式的条件） \\ =a\ast (x+3)(x-3)（使用平方差公式，因式分解完成） \end{gathered}$$

3. 立方和公式

公式：$a^3+b^3=(a+b)(a^2-ab+b^2)$

例：

$3^3+2^3=(3+2)\ast (3^2-3\ast 2+2^2)=35$

4. 立方差公式

公式：$a^3-b^3=(a-b)(a^2+ab+b^2)$

例：

$3^3-2^3=(3-2)\ast (3^2+3\ast 2+2^2)=19$

5. 完全平方公式

公式：$a^2\pm 2ab+b^2=(a\pm b{)}^2$

例：
$$\begin{gathered} m{a}^2-4ma+4m \\ =m\ast (a^2-4a+4)（先用提取公因式的方式，提取三个多项式的公共因式m） \\ =m\ast (a^2-(2\ast a\ast 2)+2^2)（a^2-(2\ast a\ast 2)+2^2满足完全平方公式的条件） \\ =m\ast (a-2{)}^2（使用完全平方公式，因式分解完成） \end{gathered}$$

6. 首一十字相乘

公式：$x^2+(a+b)x+ab=(x+a)(x+b)$

例：
$$\begin{gathered} x^2-x-12 \\ =x^2+(-1)x-12 \\ =先找到和是-1并且乘积是12的两个数，分别为-4和3 \\ =(x+3)(x-4)（直接将-4和3套入十字相乘公式，因式分解完成） \end{gathered}$$

7. 非首一十字相乘

公式：$$\begin{gathered} a{x}^2+bx+c=(a_{1}x+c_1)(a_{2}x+c_2) \\ a=a_1\ast a_2 \\ c=c_1\ast c_2 \\ b=a_1{c}_2+a_2{c}_1 \end{gathered}$$

例：
$$\begin{gathered} 8a^2+46ab+63b^2 \\ =找到8a^2系数的因数，（a_1=1,a_2=8）、（a_1=8,a_2=1）、（a_1=2,a_2=4）、（a_1=4,a_2=2） \\ =找到63b^2系数的因数，（c_1=1,c_2=63）、（c_1=63,c_2=1）、（c_1=3,c_2=21）、（c_1=21,c_2=3）、（c_1=7,c_2=9）、（c_1=9,c_2=7） \\ =分别交叉试验8a^2和63b^2的因数，让（a_1{c}_2+a_2{c}_1）=46 \\ =先试（a_1=1,a_2=8）和（c_1=1,c_2=63）交叉相乘，1\ast 8+1\ast 63不等于46 \\ =再试（a_1=2,a_2=4）和（c_1=7,c_2=9）交叉相乘，7\ast 4+9\ast 2=46，满足非首一十字相乘的条件 \\ =所以(a_{1}x+c_1)(a_{2}x+c_2)=(2a+7b)(4a+9b) \end{gathered}$$

8. 配方法

原理：利用配方法，让表达式满足完全平方公式

公式：$x^2+bx=x^2+bx+(\frac{b}{2}{)}^2-(\frac{b}{2}{)}^2=(x+\frac{b}{2}{)}^2-(\frac{b}{2}{)}^2$

例：$x^2+4x+5=x^2+4x+(\frac{5}{2}{)}^2-(\frac{5}{2}{)}^2+5=(x+\frac{5}{2}{)}^2-(\frac{5}{2}{)}^2+5$

当二次项的系数不为1时，要先将二次项的系数消除，例如：

$$\begin{gathered} 3x^2+4x+5 \\ =(3x^2\ast \frac{1}{3})+(4x\ast \frac{1}{3})+(5\ast \frac{1}{3}) \\ =x^2+\frac{4}{3}x+\frac{5}{3} \\ =（将二次项的系数变为1后，就可以使用配方法） \\ =x^2+\frac{4}{3}x+(\frac{4}{3}\ast \frac{1}{2}{)}^2-(\frac{4}{3}\ast \frac{1}{2}{)}^2+\frac{5}{3} \\ =(x+\frac{2}{3}{)}^2-(\frac{4}{3}\ast \frac{1}{2}{)}^2+\frac{5}{3} \\ =(x+\frac{2}{3}{)}^2+(-\frac{4}{9}+\frac{5}{3}) \\ =(x+\frac{2}{3}{)}^2+\frac{11}{9} \end{gathered}$$

8. 直接开平方法

公式：$a^2=\pm \sqrt{a}，等号右边不要忘了正负号$

例1：
$$\begin{gathered} (2x+1{)}^2=(5-x{)}^2 \\ 步骤1：\sqrt{(2x+1{)}^2}=\pm \sqrt{(5-x{)}^2} \\ 步骤2：2x+1=\pm (5-x) \\ 结果：x_1=\frac{4}{3}，x_2=-6 \end{gathered}$$

例2：
$$\begin{gathered} (x-2{)}^2=7 \\ 步骤1：\sqrt{(x-2{)}^2}=\pm \sqrt{7} \\ 步骤2：x-2=\pm \sqrt{7} \\ 结果：x_1=\sqrt{7}+2，x_2=-\sqrt{7}+2 \end{gathered}$$

9. 公式法和根的判别式

公式：$\frac{-b\pm \sqrt{b^2-4ac}}{2a}$

使用这个公式的前提，方程必须满足 $a{x}^2+bx+c=0$，这个结构

公式中 $b^2-4ac，也可以称作根的判别式，可以用希腊字母德尔塔（Delta）\Delta 表示$

当 $\Delta =b^2-4ac>0$ 时，表示方程有两个不等的实根
当 $\Delta =b^2-4ac=0$时，表示方程有两个相等的实根
当 $\Delta =b^2-4ac<0$时，表示方程没有实根，这个方程不需要继续计算了

例：

$$\begin{gathered} 2x^2+3x+1=6x+2 \\ 步骤1，让方程满足标准公式，所以要移项，：2x^2+3x-6x+1-2=0 \\ 步骤2，合并同类项，：2x^2-3x-1=0，这时候已经满足标准二次方程结构了 \\ 步骤3，和标准一元二次方程结构对比，a{x}^2+bx+c=0，得到a=2，b=-3，c=-1 \\ 步骤4，将abc套入根的判别式中，判断是否需要继续解方程 \\ \Delta =(-3{)}^2-4\ast 2\ast (-1)>0，说明有两个不等的实根，需要继续解方程 \\ 步骤5，拿abc直接套入公式法，\frac{-(-3)\pm \sqrt{(-3{)}^2-4\ast 2\ast (-1)}}{2\ast 2} \\ 结果，合并同类项，得到：x_1=\frac{3+\sqrt{17}}{4}，x_2=\frac{3-\sqrt{17}}{4} \end{gathered}$$

10. 根与系数的关系

当 $\Delta =b^2-4ac>=0$ 时，表示方程有两个实根，两个实根的关系如下：

两个根的和为：$x_1+x_2=-\frac{b}{a}$

两个根的乘积为：$x_1\ast x_2=\frac{c}{a}$

两个根的平方和为：$x_1^2+x_2^2=(x_1+x_2{)}^2-2\ast x_1\ast x_2$

两个根的倒数和为：$\frac{1}{x_1}+\frac{1}{x_2}=\frac{x_1+x_2}{x_1\ast x_2}$

两个根的差的绝对值为：$|x_1-x_2|=\sqrt{(x_1+x_2{)}^2-4\ast x_1\ast x_2}$

例：
已知 $$\begin{gathered} \Delta =2x^2-3x-4>0，求x_1+x_2和x_1\ast x_2 \\ 步骤1，对比标准一元二次方程结构，a{x}^2+bx+c=0，得到a=2，b=-3，c=-4 \\ 步骤2，直接套入公式：x_1+x_2=-\frac{b}{a}和x_1\ast x_2=\frac{c}{a} \\ 结果： \\ {x}_1+x_2=-\frac{-3}{2}=\frac{3}{2} \\ {x}_1\ast x_2=\frac{-4}{2}=-\frac{4}{2}=-2 \end{gathered}$$

五、函数

1. 函数

函数标准式：$y=kx，其中k是系数，k\ne 0$

2. 一次函数的标准式和图像

一次函数标准式：$y=kx+b，k是系数，k\ne 0、b为常数，b可以为0$

一次函数图像：

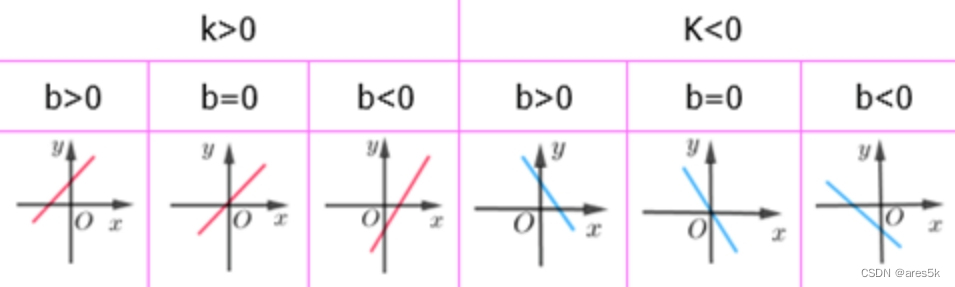
一次函数图像中，当 k 是正数时，直线是从左下到右上，当 k 是负数时，直线是从右下到左上

3. 二次函数标准式和图像

二次函数标准式：$y=a{x}^2+bx+c，其中b、c是常数可以为0，a\ne 0$

二次图像中：

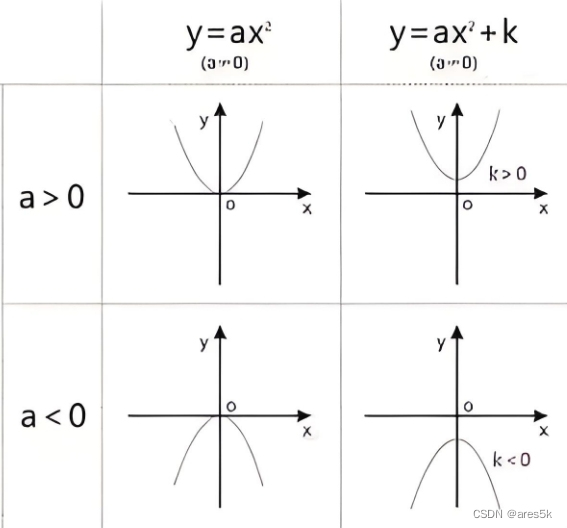
二次图像中，当 a 是正数时，抛物线开口向上，当 a 是负数时，抛物线开口向下

4. 二次函数顶点式

顶点式：$y=a(x-h{)}^2+k，对称轴：x=h时，顶点(h,k)$

5. 从标准式到顶点式

$利用提取公因式法和配方法从标准式中找到顶点式，既从a{x}^2+b+c中找到a(x-h{)}^2+k结构$

公式：
$顶点式=a(x+\frac{b}{2a}{)}^2+\frac{4ac-b^2}{4a}$
$h=-\frac{b}{2a}$
$k=\frac{4ac-b^2}{4a}$

$公式来历：$
$$\begin{gathered} a{x}^2+b+c \\ 步骤一，提取公因式a，a(x^2+\frac{b}{a})+c \\ 步骤二，利用配方法，a(x^2+\frac{b}{a}+\frac{b^2}{4a^2})-a\ast \frac{b^2}{4a^2}+c \\ 步骤三，利用完全平方公式因式分解，a(x+\frac{b}{2a}{)}^2-\frac{b^2}{4a}+c \\ 步骤三，通分后得到顶点式，a(x+\frac{b}{2a}{)}^2+\frac{4ac-b^2}{4a} \\ 结果，和顶点式a(x-h{)}^2+k比较得：h=-\frac{b}{2a},k=\frac{4ac-b^2}{4a} \end{gathered}$$

例：

$$\begin{gathered} 从2x^2+8x+5中找到h、k \\ 直接套入公式即可 \\ h=-\frac{b}{2a}=-\frac{8}{4}=-2 \\ k=\frac{4ac-b^2}{4a}=\frac{4\ast 2\ast 5-8^2}{4\ast 2}=-3 \end{gathered}$$

6. x轴的交点式

求解析式时，当题目给了两个交与x轴的坐标时，就可以使用交点式代替标准式，更快的计算

公式： $y=a(x-x_1)(x-x_2)$

例：

抛物线过点（-1，0）、（4，0）和（0，-2），求它的解析式。

解，使用交点式，更方便：

$$\begin{gathered} 步骤1：先将两个交与x的坐标套入交点式：y=a(x-(-1))(x-4)=a(x+1)(x-4) \\ 步骤2：在将未交于x点的坐标代入交点式求a：-2=a(0+1)(0-4) \\ 步骤3：得到a=\frac{1}{2} \\ 步骤4：将a代入到步骤1中的交点式：y=\frac{1}{2}(x+1)(x-4) \\ 结果：方程展开后得到一元二次函数，y=\frac{1}{2}{x}^2-\frac{3}{2}x-2 \end{gathered}$$

解，如果是用标准式，就很麻烦：

$$\begin{gathered} 设:y=a{x}^2+bx+c \\ 解3元方程组： \\ a-b+c=0 \\ 16a+4b+c=0 \\ c=-2 \end{gathered}$$

7. 一元二次方程和二次函数

$一元二次方程a{x}^2+b+c=n相当于在二次函数y=a{x}^2+b+c的图像上做一条横切线$

$当n>二次函数的顶点坐标中的y轴坐标时，横切线与二次函数图像有两个交点$

$当n=二次函数的顶点坐标中的y轴坐标时，横切线与二次函数图像有一个交点$

$当n<二次函数的顶点坐标中的y轴坐标时，横切线与二次函数图像没有交点$

8. 反比例函数的标准式和图像

反比例函数的标准式： $y=\frac{k}{x}$

反比例函数的图像：

• 当 k > 0 时：
  当 x > 0 时，图像在第一象限， 当 x < 0 时，图像在第三象限
  y 随 x 增大而减小
• 当 k < 0 时：
  当 x > 0 时，图像在第二象限， 当 x < 0 时，图像在第四象限
  y 随 x 增大而增大

一三或二四象限的图像同时出现时称作双曲线，其有两条对称轴 $y=-x和y=x$

两个双曲线的 k 如果互为相反数，那么图像关于 $x$ 轴对称

9. 反比例函数中k的几何意义

在反比例图像中任取一点，向两个轴做垂线，其组成的图形的面积公式为： $x\ast y=|k|$

例：反比例函数为 $y=\frac{4}{x}$, 在其图像的（1，4）中分别向两条轴做垂线，其围成的图形的面积是：1 * 4 = 4

10. 反比例函数图像上的点坐标乘积相等

在同一反比例函数图像上的所有点坐标的乘积都相等

例：

$(2,3)(6,1)这两个点在同一反比例函数图像上，(5,7)(1,3)这两个点就不在同一反比例函数图像上$

11. 一次、二次、反比例函数图像的平移

口诀：上加下减在末尾，左加右减在 $x$

左右平移指的是，$y$ 轴不变，$x$ 轴左右平移

上下平移指的是，$x$ 轴不变，$y$ 轴上下平移

一次函数 $y=kx+b$ 平移，例：

左移五个单位，$y=k(x+5)+b$

右移五个单位，$y=k(x-5)+b$

上移五个单位，$y=kx+b+5$

下移五个单位，$y=kx+b-5$

二次函数 $y=a{x}^2+bx+c$ 平移，例：

左移五个单位，$y=a(x+5{)}^2+b(x+5)+c$

右移五个单位，$y=a(x-5{)}^2+b(x-5)+c$

上移五个单位，$y=y=a{x}^2+bx+c+5$

下移五个单位，$y=y=a{x}^2+bx+c-5$

反比例函数 $y=\frac{k}{x}$ 平移，例：

左移五个单位，$y=\frac{k}{x+5}$

右移五个单位，$y=\frac{k}{x-5}$

上移五个单位，$y=\frac{k}{x}+5$

下移五个单位，$y=\frac{k}{x}-5$