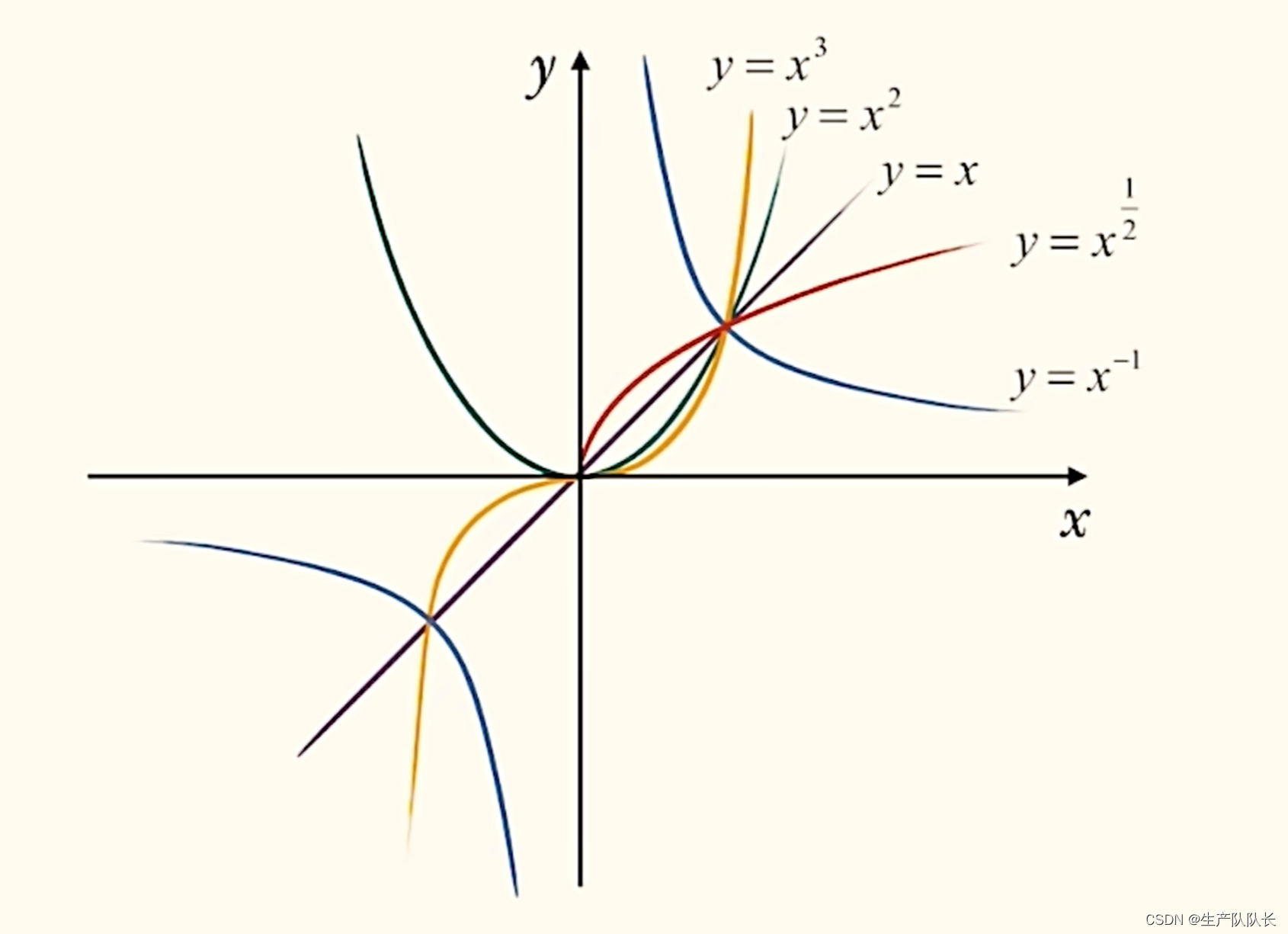
一、三大基本函数图像
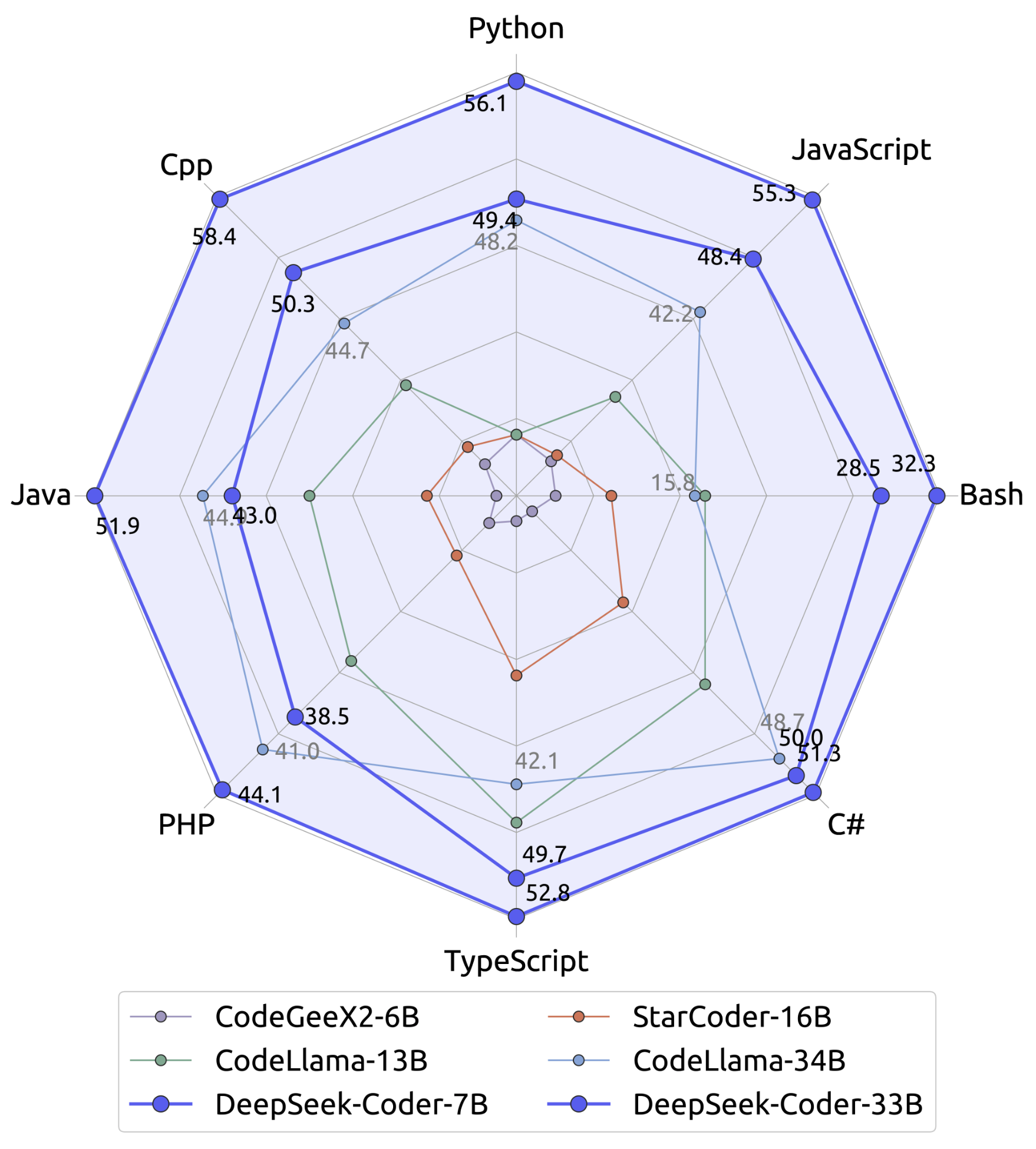
1、指数函数图像
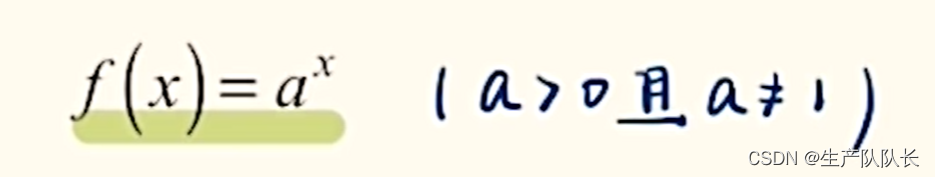

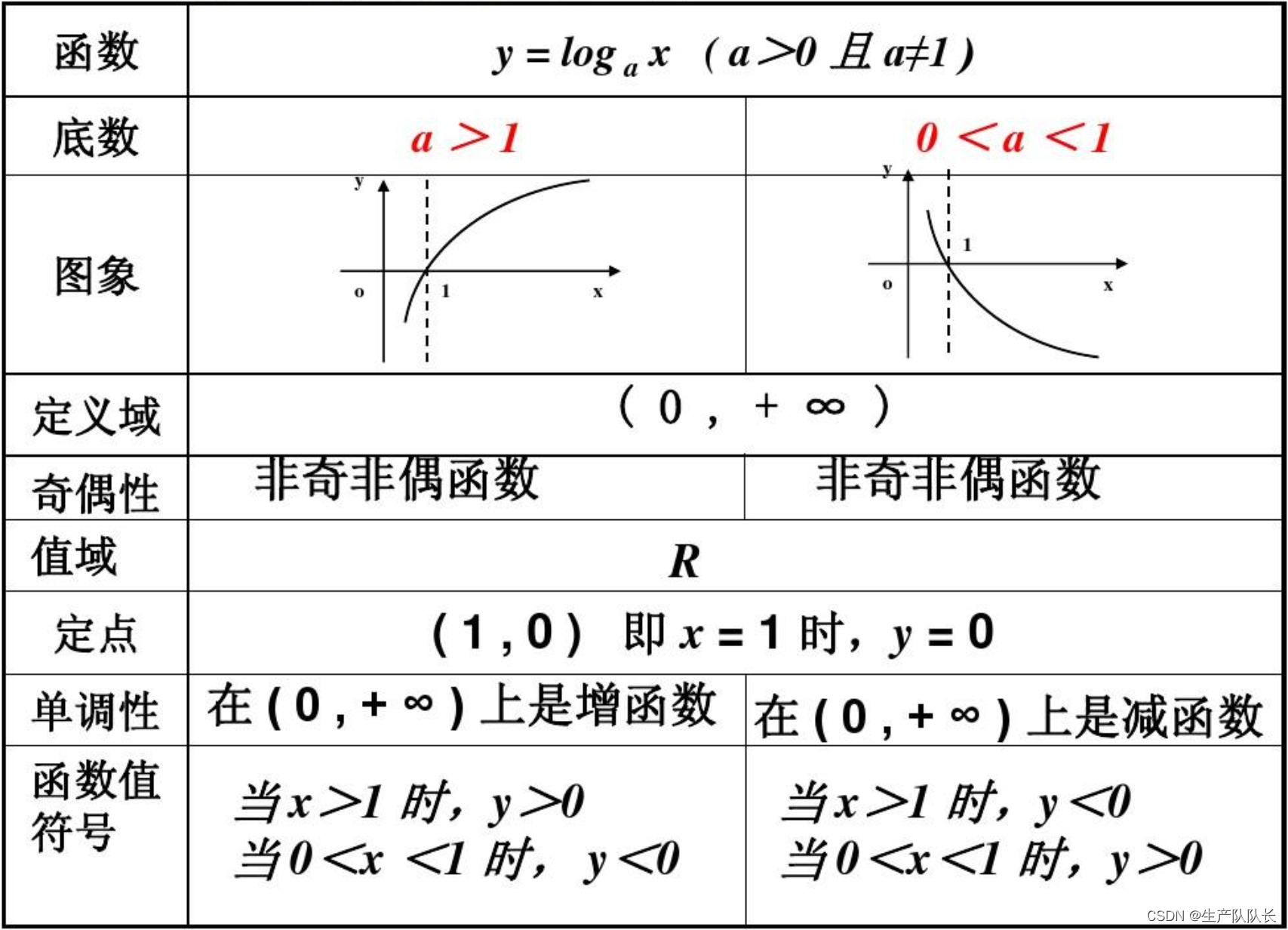
2、对数函数图像
3、幂函数图像
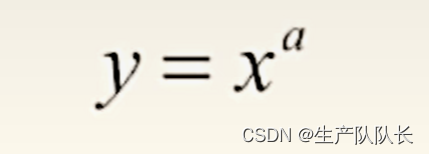
二、案例
口诀:上加下减,左加右减
1、指数函数图像变化规律
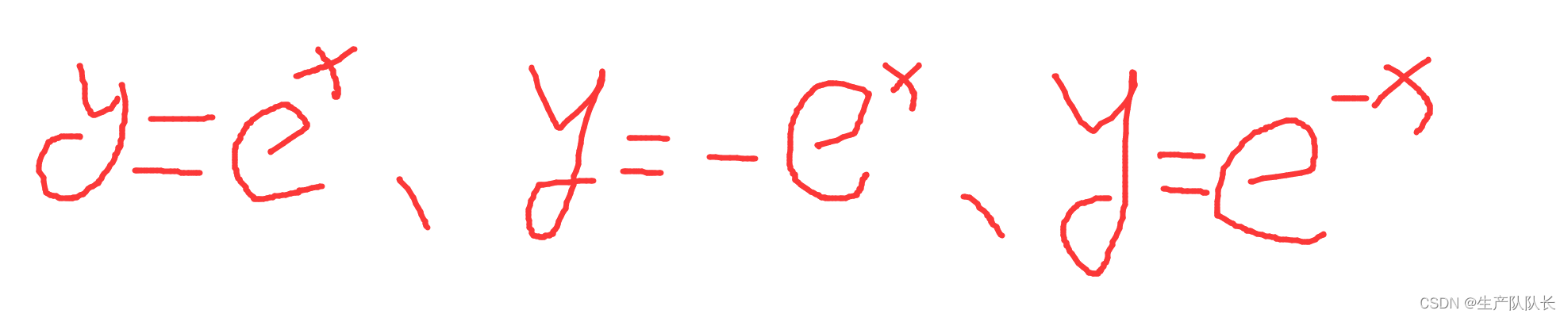
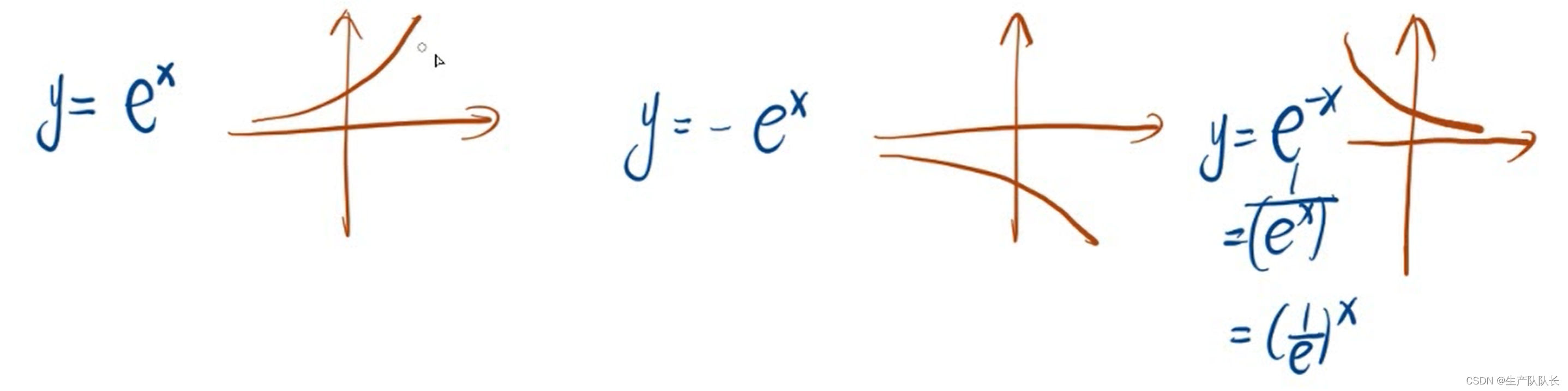
2、带绝对值的函数图像
情况1:绝对值套住整个函数表达式
画法原则:x轴下方的图像,对称到x轴上方
本例画法:
1、求定义域
2、先画出绝对值里面的指数函数图像
3、上加下减
4、x轴下方图像翻转到x轴上方
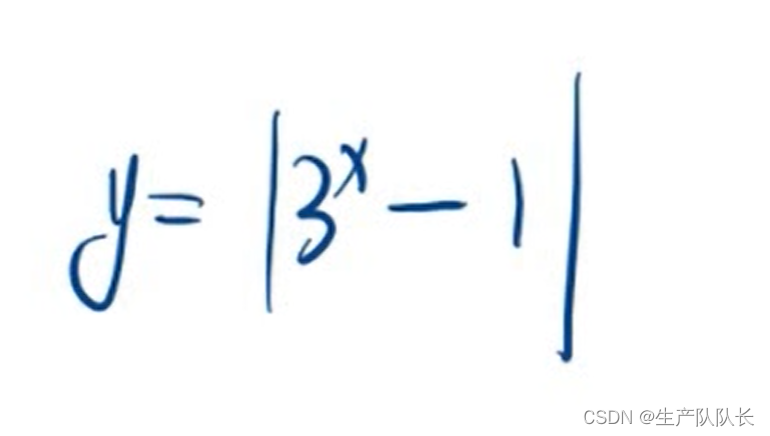

情况2:绝对值套住自变量x
画法原则:找出0点,去绝对值,分类讨论
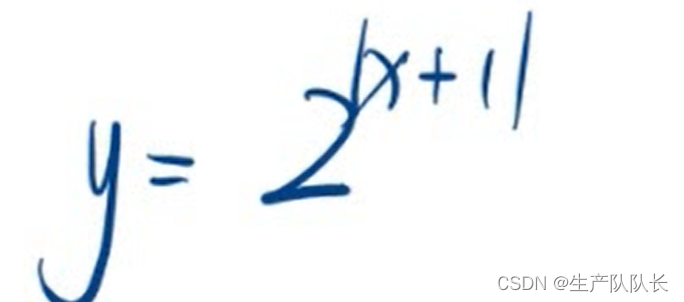
本例画法:
1、求定义域
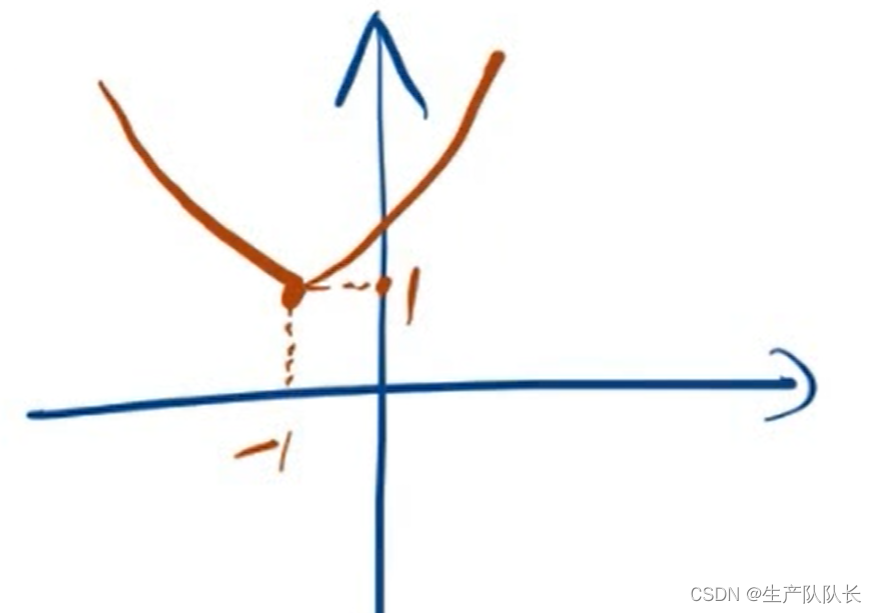
2、分区间讨论
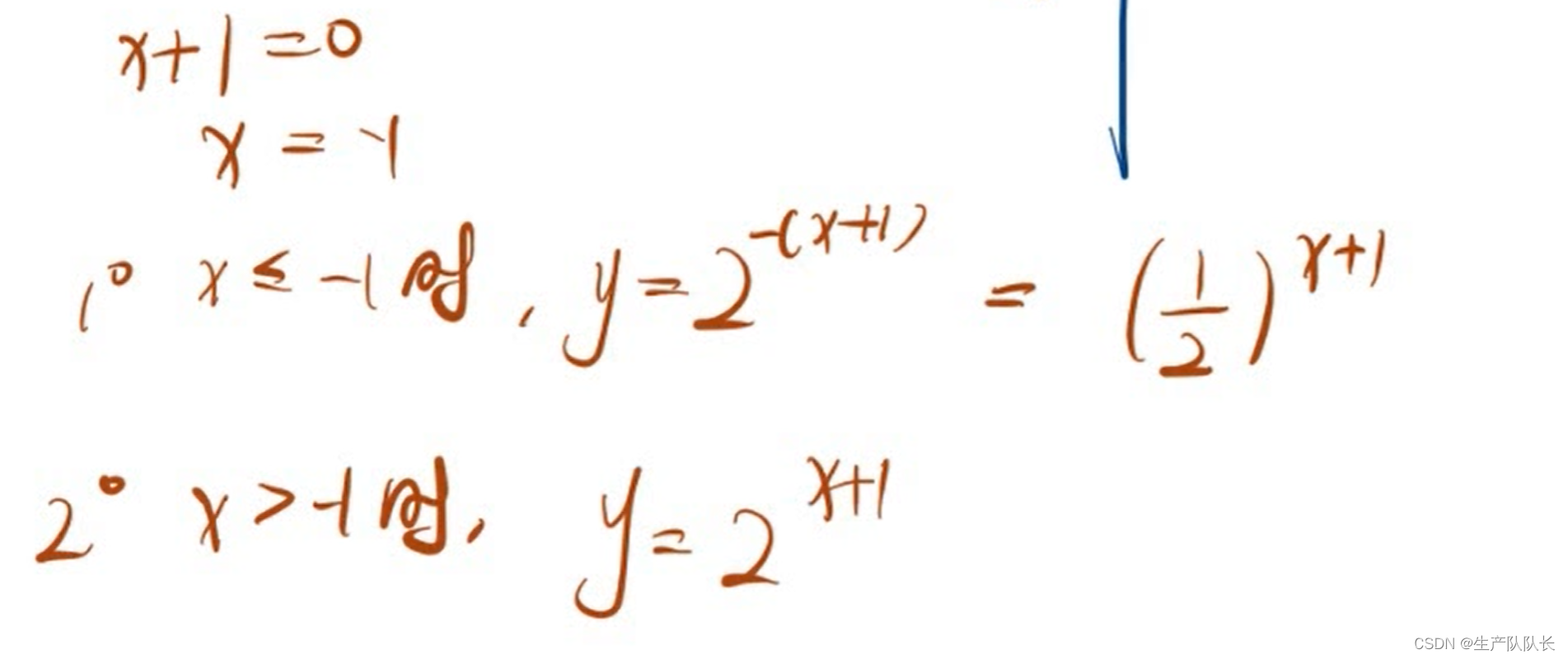
3、复杂分式函数图像画法(较难)
画法原则:对函数式变形,向我们学过的函数形式靠拢
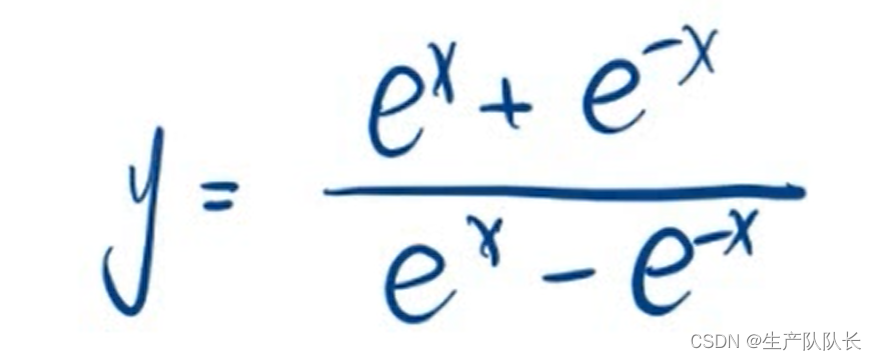
本例画法:
1、求定义域
x≠0
2、函数式变形
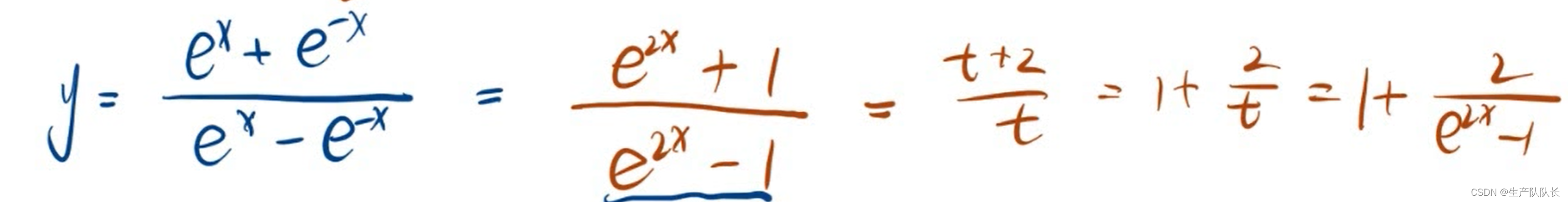
3、分定义域区间讨论
区间端点的趋近值(可以理解为,找水平和垂直渐近线)
判断区间上函数的单调性

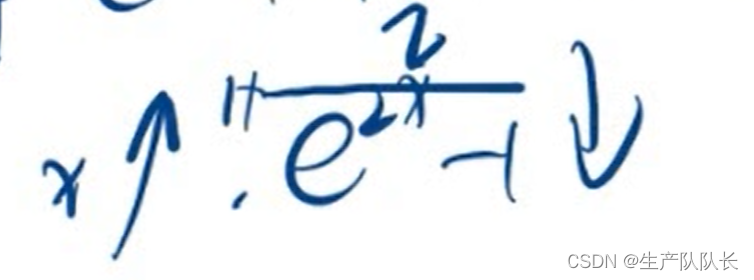


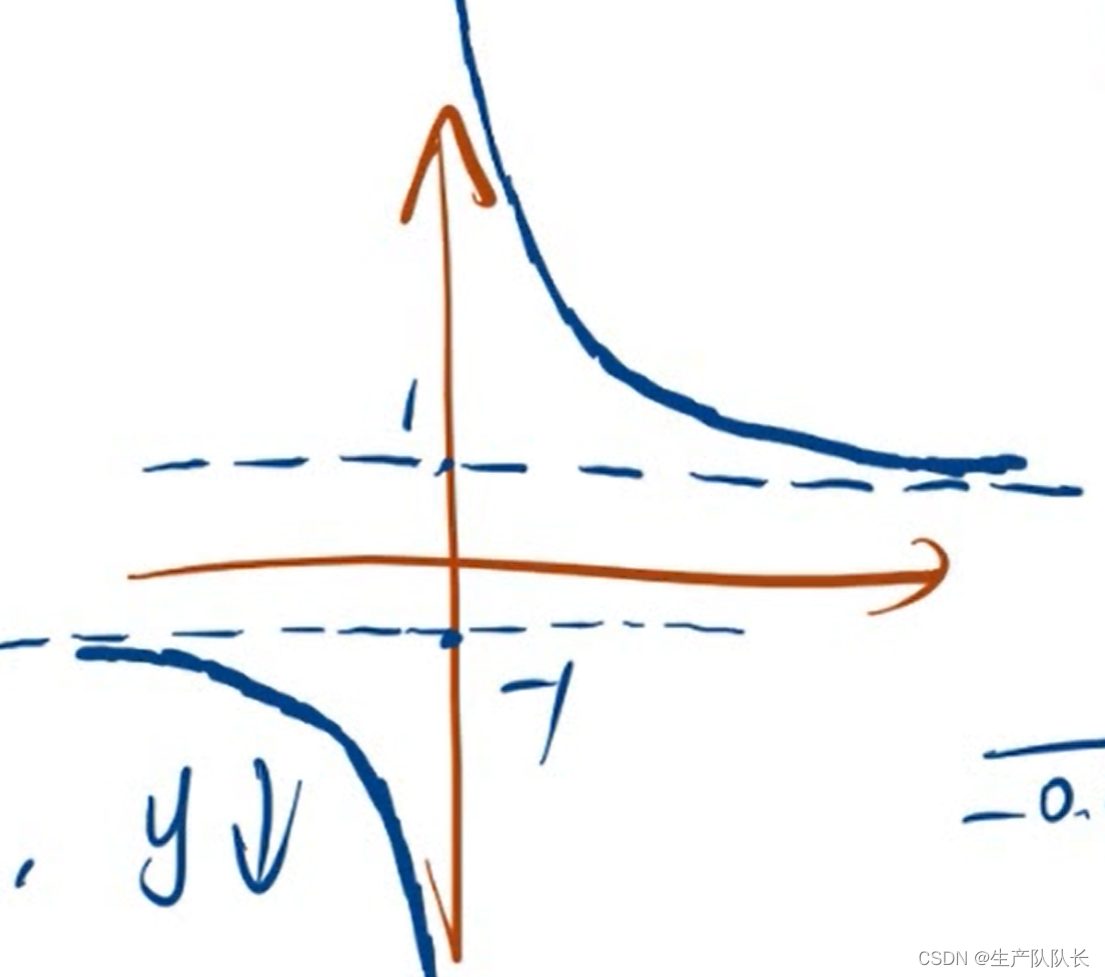
最终草图
三、画图大致步骤汇总
1、求定义域
2、判断奇偶性(可能非奇非偶)
3、上加下减,左加右减
4、函数式变形(向已经学过的函数靠拢变形,非必要步骤)
5、分区间讨论
6、讨论区间上的单调性
7、得出最终草图
四、例题
例题1

例题2