概念大合集01
- 1、数据结构基础的定义
- 2、数据结构
- 2.1 数据元素之间关系的集合
- 2.2数据结构的三要素
- 2.2.1数据的逻辑结构
- 2.2.2数据的存储(物理)结构
- 2.2.3数据的运算
- 3、数据类型
- 4、抽象数据类型类型(ADT)
- 5、算法及其描述
- 5.1算法的5个特性
- 5.2算法设计的目标
- 5.3算法的时间复杂度
- 5.3.1时间复杂度的求和、求积定理
- 5.4算法的空间复杂度
阅读指导:
本文内容丰富,涵盖广泛,读者朋友们可以根据目录指引,直接跳跃至您感兴趣的章节开始品读。此外,作者正在积极创作后续篇章,如果您对本篇文章有所喜爱,不妨点击关注,以便第一时间获取最新作品动态。
现在,让我们开始正文的旅程吧。希望您能细细品味每一个字句,如果您在任何地方发现有任何不妥或欠缺之处,请在评论区不吝赐教。作者将虚心接受您的宝贵意见,并努力进行改进。期待您的宝贵反馈!
下一篇文章
数据结构的概念大合集02(线性表)
1、数据结构基础的定义
| 名称 | 具体概念 |
|---|---|
| 数据 | 描述客观事物的数和字符的集合,能被计算机程序处理的符号总称 |
| 数据元素 | 数据的基本单位,又称元素、结点、顶点、记录 |
| 数据项 | 是具有独立含义的数据最小单位,是构成数据元素的最小单位,又称字段、域 |
| 数据对象 | 性质相同的数据元素的集合,是数据的一个子集 |
| 数据结构 | 是相互之间存在一种或多种特定关系的数据元素的集合,包括逻辑结构和物理结构 |
| 数据类型 | 是一个值的集合和定义在这个值集上的一组操作的总称 |
| 抽象数据类型 | 是指一个数学模型以及定义在该模型上的一组操作 |
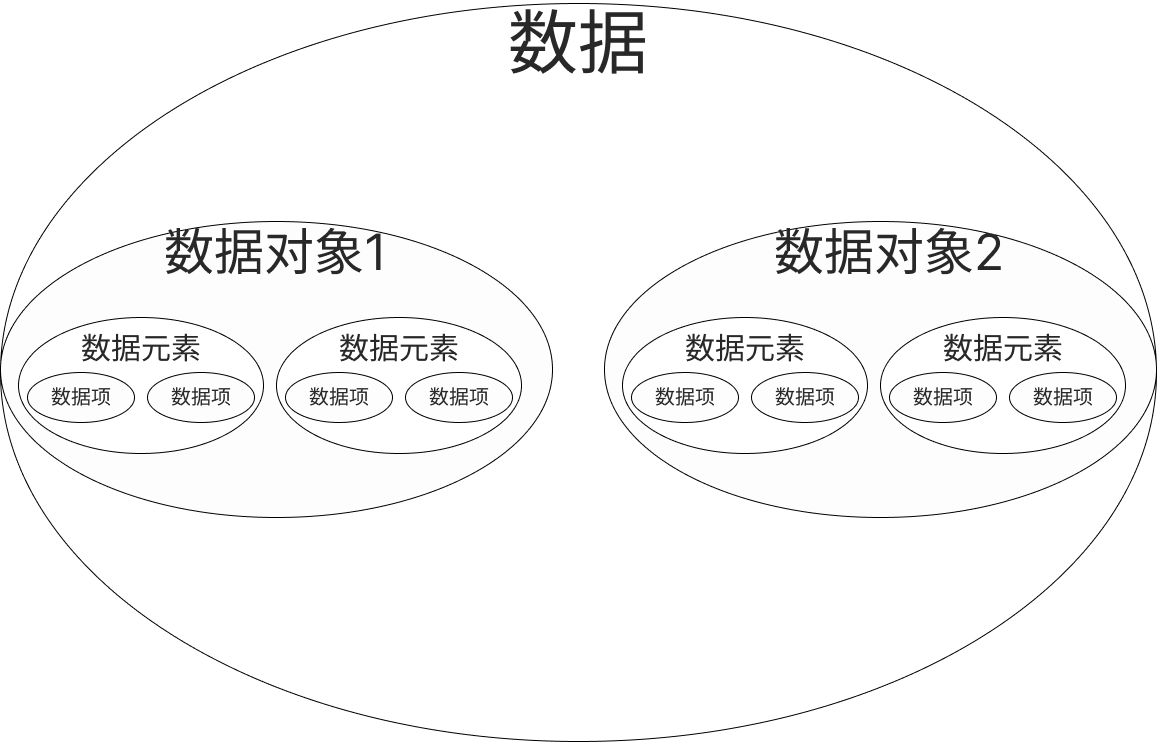
2、数据结构
2.1 数据元素之间关系的集合
| 数据的基本结构 | 关系 |
|---|---|
| 集合 | 属于同一个集合,没有什么具体关系 |
| 线性结构 | 一对一 |
| 树形结构 | 一对多 |
| 图形(网状)结构 | 多对多 |
2.2数据结构的三要素
2.2.1数据的逻辑结构
从逻辑上表示数据,与具体的存储无关
2.2.2数据的存储(物理)结构
指的是数据的逻辑结构在计算机的具体实现,依赖于计算机语言
2.2.3数据的运算
数据的运算包括运算定义和运算实现
- 运算定义:对于运算功能的描述,是抽象的,是基于逻辑关系的
- 运算实现:是程序员完成运算的实现算法,是具体的,是基于存储结构的
3、数据类型
指的是一组性质相同的值的集合和定义在此集合上的一组操作的总称
比如C语言中的int、float等。
4、抽象数据类型类型(ADT)
逻辑结构+抽象运算
定义抽象数据类型:
ADT 抽象数据类型名
{
数据对象:<数据对象的定义>
数据关系:<数据关系的定义>
基本操作:<基本操作的定义>
}
5、算法及其描述
5.1算法的5个特性
又穷性;确定性;可行性;有输入;有输出
5.2算法设计的目标
正确性;可使用性;可读性;健壮性;高效率与低存储量需求
5.3算法的时间复杂度
主要衡量的是一个算法的运行速度。为了描述一个算法的时间复杂度,人们发明了一个通用的表示方法:
「 大O符号表示法 」,即 T(n) = O(f(n))
我们先来看个例子:
for(i=1; i<=n; ++i) //第一行
{j = i; //第三行j++; //第四行
}
在大O符号表示法中,f(n)表示每行代码的执行次数之和;
所以上述代码中,第一行执行一次,第三行执行n次,第四行执行n次,整段代码执行(1+2n)次,即f(n)=1+2n;
取波极限,当n无穷大时,则令f(n)=n(注意不是2n,这是简化的写法);
于是此时T(n) = O(n);
为什么可以大O表示法可以简写呢,主要是因为这个表达式主要是表示代码执行时间的增长的变化趋势的,所以当n无穷大时,常数1和倍数2的意义就不是很大了。所以在采取大O表示法的时候,我们常取其指数最大的一项来表示,同时省略其他项和指数最大项的倍数。
常见的时间复杂度量级有:
- 常数阶O(1)
- 对数阶O(logN)
- 线性阶O(n)
- 线性对数阶O(nlogN)
- 平方阶O(n²)
- 立方阶O(n³)
- K次方阶O(n^k)
- 指数阶(2^n)
上面从上至下依次的时间复杂度越来越大,执行的效率越来越低。
5.3.1时间复杂度的求和、求积定理
T1(n) = O(f(n))
T2(n) = O(g(n))
求和:T1(n) + T2(n) = O( Max ( f(n),g(n) ) )
求积:T1(n) × T2(n) = O( f(n) × g(n) )
5.4算法的空间复杂度
空间复杂度是对一个算法在运行过程中临时占用存储空间大小的一个量度,同样反映的是一个趋势,我们用 S(n) 来定义。与上面的时间复杂度一样,也采用大O表示法。
即S(n) = O( g(n) )
举例:
- 空间复杂度O(1)
如果算法执行所需要的临时空间不随着某个变量n的大小而变化,即此算法空间复杂度为一个常量,可表示为 O(1)
举例:
int i = 1;
int j = 2;
++i;
j++;
int m = i + j;
代码中的 i、j、m 所分配的空间都不随着处理数据量变化,因此它的空间复杂度 S(n) = O(1)
- 空间复杂度O(n)
int fun(int n)
{return n < 2 ? n : fun(n - 1)*n;
}
阶乘递归函数会依次调用fun(N),fun(N-1),…,fun(2),fun(1),开辟了n个空间,所以空间复杂度为O(n) 。