【八】【算法分析与设计】双指针（2）

11. 盛最多水的容器

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

说明：你不能倾斜容器。

示例 1：

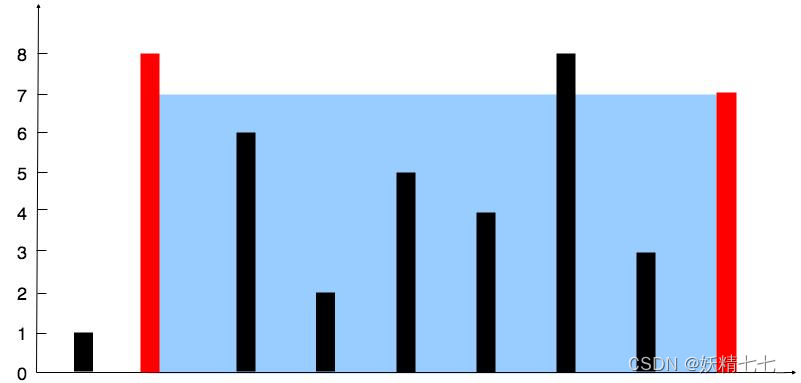
输入：[1,8,6,2,5,4,8,3,7] 输出：49 解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例 2：

输入：height = [1,1] 输出：1

提示：

n == height.length

2 <= n <= 10(5)

0 <= height[i] <= 10(4)

暴力求解：

class Solution {
public:int maxArea(vector<int>& height) {int n=height.size();int max=INT_MIN;for(int i=0;i<n;i++){for(int j=i+1;j<n;j++){max=fmax(max,(j-i)*min(height[i],height[j]));}}return max;}
};

双指针优化暴力解法：

我们首先研究一小段区间[left,right]内最大的盛水体积。

先计算left与right的最大盛水体积，记为ret。如果height[left]<=height[right]，那么对于left与任意其他下标组合，计算出来的体积都一定小于ret。因为left与其他任意下标组合（记为right1），right1-left一定小于rifht-left。而计算体积的高度是取决于高度小的那一个，高度h=min(height[right1],height[left])。体积v=(right1-left)*h。高度h=height[left]，或者h<height[left]。所以体积v一定小于ret。也就是left与其他位置下标的组合都可以不用计算。

class Solution {
public:int maxArea(vector<int>& height) {int left = 0, right = height.size() - 1, ret = 0;while (left < right) {int v = (right - left) * fmin(height[left], height[right]);ret = max(ret, v);if (height[left] <= height[right]) {left++;} elseright--;}return ret;}
};

函数接收一个整数类型的向量 height，向量的每个元素代表一个竖直线的高度，这些竖直线的宽度假设为1，函数返回由这些线形成的容器可以容纳的最大水量。

int left = 0, right = height.size() - 1, ret = 0;

初始化三个整数变量：left 设置为0，表示向量的起始索引；right 设置为 height.size() - 1，即向量的最末索引；ret 初始化为0，用于存储最大的水容量。

while (left < right) {

使用一个循环来遍历所有可能的容器。当 left 索引小于 right 索引时，循环继续。

int v = (right - left) * fmin(height[left], height[right]);

计算当前 left 和 right 索引之间形成的容器可以容纳的水量。水量由两个竖直线之间的距离（right - left）和两条线中较短一条的高度（fmin(height[left], height[right])）的乘积得出。

ret = max(ret, v);

更新 ret，使其始终保持为迄今为止找到的最大水容量。

if (height[left] <= height[right]) { left++; } else right--;

根据 left 和 right 索引处的高度比较结果，移动 left 或 right 索引。如果 left 处的高度小于等于 right 处的高度，则 left 索引向右移动（left++）；否则，right 索引向左移动（right--）。这是基于贪心算法的思想，即保留较高的竖直线以期望找到更大的水容量。

时间复杂度和空间复杂度分析

时间复杂度：O(n)，其中 n 是向量 height 的长度。这是因为我们只需要一次遍历就可以找到最大的水容量，left 从向量的起始位置向右移动，right 从向量的末尾位置向左移动，直到它们相遇。

空间复杂度：O(1)，因为我们只使用了常数级别的额外空间，即几个变量来存储索引和计算结果。

611. 有效三角形的个数

给定一个包含非负整数的数组 nums ，返回其中可以组成三角形三条边的三元组个数。

示例 1:

输入: nums = [2,2,3,4] 输出: 3 解释:有效的组合是: 2,3,4 (使用第一个 2) 2,3,4 (使用第二个 2) 2,2,3

示例 2:

输入: nums = [4,2,3,4] 输出: 4

提示:

1 <= nums.length <= 1000

0 <= nums[i] <= 1000

暴力枚举：

判断a，b，c三个数是否可以组成三角形，只需要满足a+b>c,a+c>b,b+c>a三个条件即可。如果a,b,c三个数满足a<=b<=c有序的条件，我们只需要判断a+b>c满足即可组成三角形。原因是a+c>b和b+c>a是一定成立的，因为c已经大于等于a和b了，再加上一个正数不等式一定成立。

所以我们的思路是先把nums数组排序，排序后再暴力枚举三个数。满足条件就ret++。

class Solution {
public:int triangleNumber(vector<int>& nums) {sort(nums.begin(), nums.end());int n = nums.size();int ret = 0;for (int i = 0; i < n; i++) {for (int j = i + 1; j < n; j++) {for (int k = j + 1; k < n; k++) {if (nums[i] + nums[j] > nums[k])ret++;}}}return ret;}
};

双指针优化暴力枚举：

先对nums数组排序。

研究[a,c]区间所有可以组成三角形的情况。首先固定最大的数c。记left=0，right=c-1。

对于left，right，c三个数的组合，如果nums[left]+nums[right]>c说明可以组成三角形。对于left+1，right，c三个数，一定也可以组成三角形。因为left+1>left，而函数是递增的。所以nums[left+1]>nums[left]，nums[left+1]+nums[left]>c。以此类推，对于与right的组合，一共有right-left个数可以组成三角形。考虑完与right的组合所有情况，就right--，不考虑right的组合情况了。

如果nums[left]+nums[right]<=c，说明不可以组成三角形。对于left,right-1,c三个数，一定也不可以组成三角形。因为right-1<right，而函数是递增的。所以nums[right-1]<nums[right],nums[right-1]+nums[left]<c。以此类推，对于与left的组合，都不可以组成三角形。考虑完与left的组合所有情况，就left++，不考虑left的组合情况了。

class Solution {
public:int triangleNumber(vector<int>& nums) {sort(nums.begin(), nums.end());int ret = 0, n = nums.size();for (int i = n - 1; i >= 2; i--) {int left = 0, right = i - 1;while (left < right) {if (nums[left] + nums[right] > nums[i]) {ret += right - left;right--;} else {left++;}}}return ret;}
};

首先对数组 nums 进行排序，这样我们可以利用三角形两边之和大于第三边的性质来简化问题。

int ret = 0, n = nums.size();

声明并初始化变量 ret 为0，它将用来计数可以构成三角形的三元组数量。变量 n 存储数组 nums 的大小。

for (int i = n - 1; i >= 2; i--) {

从数组的最后一个元素开始向前遍历，直到第三个元素（索引为2）。这是因为我们至少需要三个数来构成一个三角形。这个遍历的是最大的边长的所有可能。

int left = 0, right = i - 1;

在每次循环中，初始化两个指针 left 和 right，分别指向当前考察的三元组中最小元素的索引和次大元素的索引。

while (left < right) {

当 left 指针小于 right 指针时，执行循环体内的操作。这个循环用于找出在固定最大边 nums[i] 的情况下，有多少对 (nums[left], nums[right]) 能与 nums[i] 构成三角形。

if (nums[left] + nums[right] > nums[i]) { ret += right - left; right--; } else { left++; }

如果 nums[left] 和 nums[right] 之和大于 nums[i]，则说明找到了一组有效的三元组，因为数组已经排序，所以从 left 到 right 之间的所有数都可以与 nums[right] 和 nums[i] 构成三角形。因此，将 right - left 的值累加到 ret 中，然后将 right 指针向左移动一位，以考察下一对可能的三元组。否则，如果两数之和不大于 nums[i]，与left的所有组合都无法组成三角形，则将 left 指针向右移动一位，增大两数之和的值。

时间复杂度和空间复杂度分析

时间复杂度：O(n^2)，其中 n 是数组 nums 的长度。这是因为我们首先对数组进行了排序，这需要 O(n log n) 的时间。之后，我们有一个外层循环（O(n)）和一个内层循环（O(n)），外层和内层循环的组合将会产生 O(n^2) 的时间复杂度。

空间复杂度：O(log n)，这是排序所需要的空间复杂度。除了排序之外，我们只使用了几个变量来存储索引和计算结果。

LCR 179. 查找总价格为目标值的两个商品

购物车内的商品价格按照升序记录于数组 price。请在购物车中找到两个商品的价格总和刚好是 target。若存在多种情况，返回任一结果即可。

示例 1：

输入：price = [3, 9, 12, 15], target = 18 输出：[3,15] 或者 [15,3]

示例 2：

输入：price = [8, 21, 27, 34, 52, 66], target = 61 输出：[27,34] 或者 [34,27]

提示：

1 <= price.length <= 10^5

1 <= price[i] <= 10^6

1 <= target <= 2*10^6

暴力枚举：

class Solution {
public:vector<int> twoSum(vector<int>& price, int target) {int n = price.size();for (int i = 0; i < n; i++) {for (int j = i + 1; j < n; j++) {if (price[i] + price[j] == target)return {price[i], price[j]};}}return {-1, -1};}
};

双指针优化暴力枚举：

只考虑[left,right]区间内的数据。

如果price[left]+price[right]>target，那么对于right与其他位置的数据的组合，一定也大于target，因为函数是递增的。因此对于right与其他位置的数据不需要再考虑。right--。

如果price[left]+price[right]<target，那么对于left与其他位置的数据的组合，一定也小于target，因为函数是递增的。因此对于left与其他位置的数据不需要再考虑，left++。

class Solution {
public:vector<int> twoSum(vector<int>& price, int target) {int left = 0, right = price.size() - 1;while (left < right) {int sum = price[left] + price[right];if (sum > target) {right--;} else if (sum < target) {left++;} elsereturn {price[left], price[right]};}return {-1, -1};}
};

int left = 0, right = price.size() - 1;

初始化两个指针 left 和 right，分别指向数组 price 的开始和结束位置。

while (left < right) {

使用一个循环来查找两个数。当 left 指针小于 right 指针时，循环继续。

int sum = price[left] + price[right];

计算 left 和 right 指针指向的两个数的和。

if (sum > target) { right--;

如果计算出的和大于 target，则将 right 指针向左移动，以减小和的值。对于right与其他任何位置的组合，sum一定也大于target，所以不需要再考虑与right有关的组合。

} else if (sum < target) { left++;

如果计算出的和小于 target，则将 left 指针向右移动，以增大和的值。对于left与其他任何位置的组合，sum一定也小于target，所以不需要再考虑与left有关的组合。

} else return {price[left], price[right]};

如果计算出的和等于 target，则返回一个包含这两个数的数组。

return {-1, -1};

如果在循环结束时没有找到符合条件的两个数，则返回 {-1, -1}。这个操作是为了迎合编译器，因为题目意思显然是一定存在两个数之和为target。因此在while语句中一定会返回，但是如果不在外面写return，编译器会认为这个代码可能存在无返回值。因此在外面也写return是为了迎合编译器。

时间复杂度和空间复杂度分析

时间复杂度：O(n)，其中 n 是数组 price 的长度。这是因为我们使用了双指针方法遍历数组，每个元素最多被访问一次。

空间复杂度：O(1)，因为我们只使用了常数级别的额外空间，即几个变量来存储索引和计算结果，不需要额外的空间来存储数据。