信息学竞赛CSP中组合数学知识进阶及经典题目

组合数学

组合数卷积（范德蒙德卷积）

$\sum_{i=0}\limits^k\dbinom{n}{i}\dbinom{m}{k-i}=\dbinom{n+m}{k}$

组合意义：有 $n$ 个红球以及 $m$ 蓝球，选出 $i$ 个红球，再选出 $k - i$ 个蓝球，等价于有 $n$ 个红球和 $m$ 个蓝球，任意选出 $k$ 个球
$\sum_{i=0}^k\limits\dbinom{i}{n}\dbinom{k-i}{m}=\dbinom{k+1}{n+m+1}$
组合意义：有 $k + 1$ 个球排成一排，先选择一个球涂成绿色，然后在绿球的左边的所有球中选出 $n$ 个涂成红色，绿色右边的所有球中选出 $m$ 个涂成蓝色，等价于有 $k + 1$ 个球排成一排，选出 $n + m + 1$ 个球。

组合数前缀和

$\dbinom{0}{m}+\dbinom{1}{m}+\dots+\dbinom{n}{m}=\dbinom{n+1}{m+1}$

组合意义：对于 $n + 1$ 个球，选择其中一个涂红，再在红球的左边选择 $m$ 个涂蓝，等价于在 $n + 1$ 个球中，选择 $m + 1$ 。
$f(n,m)=\binom{n}{0}+\binom{n}{1}+\dots+\binom{n}{m}$
无法快速计算 $f (n, m)$ ，但是可以 $O (n)$ 算出 $f(0\sim n,m)$

计算方式：

$\begin{align*} &f(n,m)&=&\sum\limits_{i=0}^m\dbinom{n}{i}\\ &&=&\sum_{i=0}^m(\dbinom{n-1}{i}+\dbinom{n-1}{i-1}) \\ &&=&\sum_{i=0}^m\dbinom{n-1}{i}+\sum_{i=0}^{m-1}\dbinom{n-1}{i}\\ &&=&2\sum_{i=0}^m\dbinom{n-1}{i}-\dbinom{n-1}{m}\\ &&=&2f(n-1,m)-\dbinom{n-1}{m} \end{align*}$

其中 $②$ 式为组合恒等式： $\dbinom{n}{m}=\dbinom{n-1}{m}+\dbinom{n-1}{m-1}$

其中 $③$ 式后项的 $i$ 并非上式的 $i$ ，而是 $i - 1$ ，所以上界的范围是到 $m - 1$

$\mathrm{CF1327E - Count\ The\ Blocks}$

$\mathrm{Description}$

给定正整数 $n$ 。

对于一个数 $t$ ，定义一个块是 $t$ 中的连续相等的一串数字。写下 $0\cdots10^n-1$ 的所有数，不足 $n$ 位的用前导 $0$ 补足 $n$ 位。

对于每个 $i=1\cdots n$ ，求这 $10^n$ 个数中一共有多少个长为 $i$ 的块。

$\mathrm{Solution}$

分类讨论：

$i = n$ 时，答案为 $10$ ，即全部相同，只有 $10$ 种选法
$i < n$ 时
- 当长度为 $i$ 的连通块位于两边时： $10\times 9\times 10^{n-i-1}$
- 当长度为 $i$ 的连通块位于中间时： $10\times9^2\times 10^{\max(0,n-i-2)}$

$\mathrm{Accepted\ Code}$

#include <bits/stdc++.h>
#define int long longusing namespace std;typedef pair<int, int> PII;
typedef long long LL;const int MOD = 998244353;int ksm(int a, int b, int p)
{int Result = 1;while (b){if (b & 1) Result = Result * a % p;a = a * a % p;b >>= 1;}return Result;
}signed main()
{cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);int N;cin >> N;for (int i = 1; i <= N; i ++)if (i == N) cout << 10 << " ";else if (i == N - 1) cout << 10 * 9 * ksm(10, N - i - 1, MOD) * 2 % MOD << " ";else cout << (10 * 9 * ksm(10, N - i - 1, MOD) * 2 % MOD + (N - i - 1) * 10 * 9 * 9 % MOD * ksm(10, max(0ll, N - i - 2), MOD) % MOD) % MOD << " ";return 0;
}

$\mathrm{CF1761D - Carry\ Bit}$

$\mathrm{Description}$

定义 $f (a, b)$ 表示二进制下计算 $a + b$ 的进位次数。

给定 $n, k$ ，计算共有多少二元组 $(a,b)(0\le a,b\le 2^n)$ 满足 $f (a, b) = k$

$0\le k<n\le 10^6$

$\mathrm{Solution}$

首先，考虑一个暴力 DP：设 $f_{i,j,0/1}$ 表示对于前 $i$ 位，总共进位次数为 $j$ ，当前是否进位。

则有：
$\begin{align*} f_{i+1,j,0}&=3f_{i,j,0}+f_{i,j,1}\\ f_{i+1,j+1,1}&=f_{i,j,0}+3f_{i,j,1} \end{align*}$
那么，若当前用 $x$ 表示是否进位，则有 $3$ 的贡献保持不变， $1$ 的贡献发生翻转，转移路线如图：

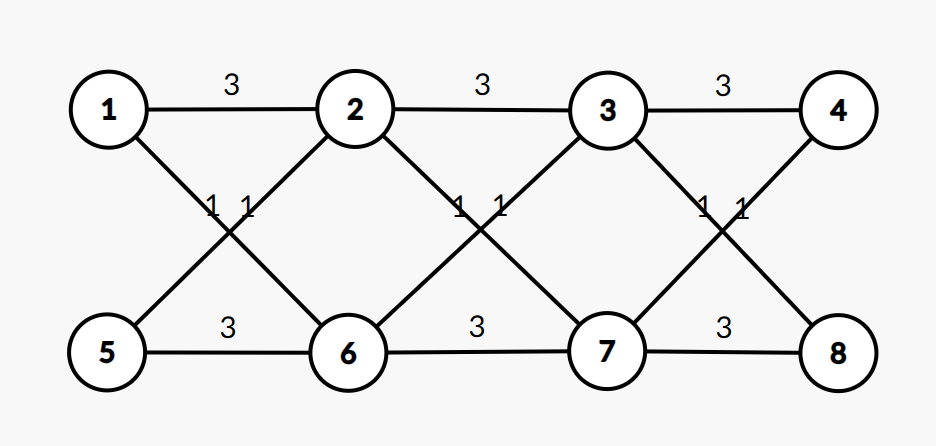
请添加图片描述

如图所示，斜边表示翻转，横边表示保持原有状态，那么转移其实就是这上面的一条条路径。（第一行为不进位，第二行为进位）

若对于一条 $01$ 路径，进位的次数是多少呢？其实是路径上 $1$ 的个数。

那么，考虑枚举路径上 $01$ 翻转的次数，记作 $i$ 。则路径上 $1$ 的极大连通块的数量 $\lceil \frac{i}{2}\rceil$ ，由于总共分成的连通块数量为 $i + 1$ ，所以 $0$ 的极大连通块数量为 $i+1-\lceil\frac{i}{2}\rceil$ 。那么，由于需要 $1$ 的个数为 $K$ ，那么加上初始状态 $0$ （没有进位），总共 $n + 1$ 个状态，这其中有 $K$ 个为 $1$ ，那么就有 $n + 1 - K$ 个为 $0$ 。

综上所述， $01$ 路径的数量应为将 $K$ 个 $1$ 划分成 $\lceil \frac{i}{2}\rceil$ 段的数量乘 $n + 1 - K$ 个 $0$ 划分成 $i+1-\lceil\frac{i}{2}\rceil$ 段的数量，通过隔板法可得： $\dbinom{n-K}{i-\lceil\frac{i}{2}\rceil}\dbinom{K-1}{\lceil \frac{i}{2}\rceil}$

不过，不要忘记对于保持不变，还有 $3$ 的转移系数，所以还要乘 $3^{n-i}$ 。

最终式子：
$\sum_{i=0}^n 3^{n-i}\dbinom{n-K}{i-\lceil\frac{i}{2}\rceil}\dbinom{K-1}{\lceil \frac{i}{2}\rceil}$

$\mathrm{Accepted\ Code}$

#include <bits/stdc++.h>
#define int long longusing namespace std;typedef pair<int, int> PII;
typedef long long LL;const int MAXN = 1e6 + 10, MOD = 1e9 + 7;int N, K;
int inv[MAXN], fact[MAXN], infact[MAXN], P3[MAXN];int C(int n, int m) { return m > n ? 0 : fact[n] * infact[m] % MOD * infact[n - m] % MOD; }signed main()
{cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);cin >> N >> K;inv[1] = 1;for (int i = 2; i <= N; i ++)inv[i] = (MOD - MOD / i) * inv[MOD % i] % MOD;fact[0] = infact[0] = P3[0] = 1;for (int i = 1; i <= N; i ++)fact[i] = fact[i - 1] * i % MOD, infact[i] = infact[i - 1] * inv[i] % MOD, P3[i] = P3[i - 1] * 3 % MOD;if (!K){cout << P3[N] << endl;return 0;}int res = 0;for (int i = 0; i <= N; i ++)res = (res + P3[N - i] * C(N - K, i + 1 - (i + 1) / 2 - 1) % MOD * C(K - 1, (i + 1) / 2 - 1) % MOD) % MOD;cout << res << endl;return 0;
}

$\mathrm{[ABC134F] Permutation\ Oddness}$

$\mathrm{Description}$

定义一个 $\sim n$ 的排列 $p$ 的「怪异度」为
$\sum_{i=1}^n|p_i-i|$
求「怪异度」为 $k$ 的 $\sim n$ 的排列数，答案对 $10^9+7$ 取模。

$\mathrm{Solution}$

对于排列计数的问题，最为困难的地方在于如何去一一对应的计算排列数。

对于本题，将题目形式化为有 $n$ 只老鼠，以及 $n$ 个洞，老鼠去找洞（一个洞只能留一只老鼠），最终的「怪异度」为老鼠走过的距离，即每条边走过的次数之和。

那么，考虑对于位置 $i$ ，老鼠 $i$ 可以去找 $< i$ 的洞，也可以找 $> i$ 的洞（洞也是类似的）。不过，如果一只老鼠找 $> i$ 的洞，那么也必有一个 $> i$ 的老鼠找 $< i$ 的洞，即是选择是对称的。

所以，不妨设 $f_{i,j,k}$ 表示前 $i$ 只老鼠，有 $j$ 只老鼠（也是 $j$ 个洞，因为是对称的）是去找 $> i$ 的位置的，目前的和为 $k$ 。

当 $f_{i,j,k}$ 转移到 $i + 1$ 的时候，那么 $i\leftrightarrow i+1$ 这条边会被经过 $2 j$ 次，因为 $j$ 只 $\le i$ 老鼠取 $> i$ 的位置， $j$ 个洞会有 $j$ 只 $> i$ 的老鼠所找到，所以会被经过 $2 j$ 次。

那么，接下来分类讨论 $j$ 的变化：

若 $i + 1$ 号老鼠和洞都是向 $> i + 1$ 的位置匹配的，那么 $f_{i,j,k}\rightarrow f_{i+1,j+1,k+2j}$ ，因为会多一对。
若 $i + 1$ 号老鼠和洞有一个向 $> i + 1$ 的位置匹配，由于一个匹配好，另一个多出未匹配的一个，一消一加，刚好抵消掉，所以 $j$ 不变，那么：
- $f_{i,j,k}\times j\rightarrow f_{i+1,j,k+2j}$ ，老鼠向 $> i + 1$ 的位置匹配，洞会选择一个 $\le i+1$ 的老鼠，此时有 $j$ 只老鼠是还未匹配的，所以任选一个，要乘 $j$ 。
- $f_{i,j,k}\times j\rightarrow f_{i+1,j,k+2j}$ ，洞向 $> i + 1$ 的位置匹配，后面分析完全一样
若 $i + 1$ 号老鼠和洞都与 $\le i+1$ 的位置匹配，那么老鼠有 $j$ 种选择，洞有 $j$ 种选择，乘法原理总共是 $j^2$ 种，那么 $f_{i,j,k}\times j^2\rightarrow f_{i+1,j-1,k+2j}$ 。
若 $i + 1$ 号老鼠与 $i + 1$ 号洞匹配，那么 $j$ 不变： $f_{i,j,k}\rightarrow f_{i+1,j,k+2j}$

综上所述，转移分如下 $3$ 种：

$f_{i,j,k}\rightarrow f_{i+1,j+1,k+2j}$
$f_{i,j,k}\times (2j+1)\rightarrow f_{i+1,j,k+2j}$
$f_{i,j,k}\times j^2\rightarrow f_{i+1,j-1,k+2j}$

$\mathrm{Accepted\ Code}$

#include <bits/stdc++.h>
#define int long longusing namespace std;typedef pair<int, int> PII;
typedef long long LL;const int MAXN = 55, MOD = 1e9 + 7;int n, m;
int f[MAXN][MAXN][MAXN * MAXN];void add(int &a, int b) { a = (a + b) % MOD; }signed main()
{cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);cin >> n >> m;f[0][0][0] = 1;for (int i = 0; i <= n; i ++)for (int j = 0; j <= i; j ++)for (int k = 0; k <= m; k ++){add(f[i + 1][j + 1][k + 2 * j], f[i][j][k]); //洞与老鼠均与 > i 的老鼠与洞匹配add(f[i + 1][j][k + 2 * j], f[i][j][k] * (2 * j + 1) % MOD); //洞或老鼠中的一个与 > i 的位置匹配，令一个匹配内部；或该洞与该老鼠匹配if (j) add(f[i + 1][j - 1][k + 2 * j], f[i][j][k] * j * j); //均与 < i 且未匹配的点匹配}cout << f[n][0][m] << endl;return 0;
}

$\mathrm{CF1838E - Count\ Supersequences}$

$\mathrm{Description}$

给定一个长为 $n$ 的序列 $a$ ， $\forall i\in[1,n],a_i\in[1,k]$ ，有序列 $b$ ，满足 $a$ 是 $b$ 的子序列， $b_i \in [1,k]$ 且 $b$ 的长度为 $m$ 。

求满足条件的 $b$ 数组个数。

$\mathrm{Solution}$

首先，考虑如何判断序列 $A$ 是序列 $B$ 的子序列，那么贪心的考虑必定是先找到 $A_1$ 在 $B$ 中出现的最早的位置 $p_1$ ， $A_2$ 在 $B$ 序列出现的最早的位置 $p_2$ ，使得 $p_2>p_1$ ， $\dots$ ， $A_n$ 在 $B$ 序列出现最早的位置 $p_n$ ，使得 $p_n>p_{n-1}$ 。

那么，这个问题是给定子序列 $A$ ，求解有多少序列 $B$ ，使得 $A$ 是 $B$ 的子序列。一个 $N ai v e$ 的想法是在 $A$ 序列每个位置前后插入数（类似隔板法），不过这样会算重。

那么，类似上面求子序列的过程，可以通过类似枚举 $p$ 序列的方式来计数：
$\sum_{p_1<p_2<\dots<p_n} (k-1)^{p_n-n}k^{m-p_n}$
一个最暴力的式子， $k - 1$ 是因为前 $p_n$ 个数每个可以选择的位置（共 $p_n-n$ 个），都不能与后面接下来的 $p$ 所对应的数重复，如果重复了，那么按照我们贪心的选择，必定会将 $p$ 选择到该位置，所以只能填 $k - 1$ 个数，但是 $p_n$ 后面的数就无所谓了！

继续狂推式子：
$\begin{align*} &\sum_{p_1<p_2<\dots<p_n} (k-1)^{p_n-n}k^{m-p_n}\\ =&\sum_{p_n=n}^m\binom{p_n-1}{n-1}(k-1)^{p_n-n}k^{m-p_n}\\ =&\sum_{p_n=n}^m\binom{p_n-1}{n-1}(k-1)^{p_n-n}\sum_{i=0}^{m-p_n}\binom{m-p_n}{i}(k-1)^{m-p_n-i}\\ =&\sum_{p_n=n}^m\sum_{i=0}^{m-p_n}\binom{p_n-1}{n-1}\binom{m-p_n}{i}(k-1)^{m-p_n-i+p_n-n}\\ =&\sum_{p_n=n}^m\sum_{i=0}^{m-p_n}\binom{p_n-1}{n-1}\binom{m-p_n}{i}(k-1)^{m-n-i}\\ =&(k-1)^m\sum_{i=0}^{m}(k-1)^{-n-i}\sum_{p_n=n}^m\binom{p_n-1}{n-1}\binom{m-p_n}{i}\\ =&(k-1)^m\sum_{i=0}^{m}(k-1)^{-n-i}\binom{m}{n+i}\\ =&(k-1)^m\sum_{i=n}^{m}(k-1)^{-i}\binom{m}{i}\\ =&\sum_{i=n}^{m}(k-1)^{m-i}\binom{m}{i}\\ \end{align*}$
好，在一番辛苦的推倒下也是成功的推到了一个简单的式子，不过还是得 $O (m)$ 做，还是过不去。我们先来讲解一下式子的含义吧：

第一步，由于后面只跟 $p_n$ 有关，所以只用枚举 $p_n$ ，剩余的 $p_{1\sim n-1}$ ，可以用组合数算，即在 $p_n-1$ 个位置里选 $n - 1$ 个数
第二步，通过二项式定理将 $k^{m-p_n}$ 化为 $k-1)+1)^{m-p_n}$
第三步，将第二个 $\sum$ 提到前面，并将两个 $(k - 1)$ 的指数次幂合并
第四步，化简 $(k - 1)$ 的指数次幂
第五步，将 $k-1)^{m-n-i}$ 替换为 $k-1)^m(k-1)^{-n-i}$ ，并将 $k-1)^m$ 提前， $k-1)^{-n-i}$ 放置在第一个 $\sum$ 的后面
第六步，观察发现后面的两个组合数相乘，其实可以用上文的组合数卷积，因为上指标的和总是一个定值。
第七步，将 $i$ 替换为 $i + n$
第八步，将 $k-1)^m$ 再合并回 $k-1)^{-i}$ 得到 $k-1)^{m-i}$

那么，如何继续优化呢？观察可知，如果 $\sum$ 的 $i$ 总 $0$ 开始枚举，其实就是二项式定理，那么不妨令其从 $0$ 开始，后面在减去即可：
$\begin{align*} &\sum_{i=n}^{m}(k-1)^{m-i}\binom{m}{i}\\ =&\sum_{i=0}^m(k-1)^{m-i}\binom{m}{i}-\sum_{i=0}^{n-1}(k-1)^{m-i}\binom{m}{i}\\ =&k^m-\sum_{i=0}^{n-1}(k-1)^{m-i}\binom{m}{i} \end{align*}$
这样，我们就可以在 $O(n\log m)$ 的时间复杂度内解决该问题了！

$\mathrm{Accepted\ Code}$

#include <bits/stdc++.h>
#define int long longusing namespace std;typedef pair<int, int> PII;
typedef long long LL;const int MOD = 1e9 + 7;int ksm(int a, int b, int p)
{int Result = 1;while (b){if (b & 1) Result = Result * a % p;a = a * a % p;b >>= 1;}return Result;
}void solve()
{int n, m, k, a;cin >> n >> m >> k;for (int i = 1; i <= n; i ++)cin >> a;int res = (ksm(k, m, MOD) - ksm(k - 1, m, MOD) + MOD) % MOD, up = 1, dw = 1;for (int i = 1; i < n; i ++){up = up * (m - i + 1) % MOD, dw = dw * ksm(i, MOD - 2, MOD) % MOD;res = (res - (up * dw % MOD * ksm(k - 1, m - i, MOD) % MOD) + MOD) % MOD;}cout << res << endl;
}signed main()
{cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);int Data;cin >> Data;while (Data --)solve();return 0;
}